Wolfram Function Repository
Instant-use add-on functions for the Wolfram Language
Function Repository Resource:
Represent the abstract product of an arbitrary collection of objects in an abstract category
ResourceFunction["AbstractProduct"][ob,prod,proj,comp,id] represents the abstract product of the collection of objects ob, with product symbol prod, projection morphism names proj, composition symbol comp and identity symbol id. | |
ResourceFunction["AbstractProduct"][…,obuniv,morphuniv,morphuniq] represents an abstract product with a universal property characterized by the universal object obuniv, universal morphisms morphuniv and unique morphism morphuniq. | |
ResourceFunction["AbstractProduct"][assoc] represents an abstract product using the association of object list, product symbol, projection morphism list, composition symbol, identity symbol, universal object, universal morphism list and unique morphism assoc. | |
ResourceFunction["AbstractProduct"][…][AbstractCategory[…]] embeds an abstract product into the specified abstract category. | |
ResourceFunction["AbstractProduct"][ResourceFunction["AbstractProduct"][…],prod,comp,id] makes a new abstract product from an old product by imposing new product symbol prod, new composition symbol comp and new identity symbol id. |
| "Objects" | list of objects in the abstract product |
| "ObjectCount" | number of objects in the abstract product |
| "MorphismAssociation" | association of morphism names/edges in the abstract product |
| "MorphismNames" | list of names of morphisms in the abstract product |
| "MorphismEdges" | list of directed edges associated to morphisms in the abstract product |
| "MorphismCount" | number of morphisms in the abstract product |
| "SimpleMorphismAssociation" | association of morphism names/edges in the abstract product with self-loops removed |
| "SimpleMorphismNames" | list of names of morphisms in the abstract product with self-loops removed |
| "SimpleMorphismEdges" | list of directed edges associated to morphisms in the abstract product with self-loops removed |
| "SimpleMorphismCount" | number of morphisms in the abstract product with self-loops removed |
| "UniversalObjects" | list of objects in the abstract product characterizing the universal property |
| "UniversalObjectCount" | number of objects in the abstract product characterizing the universal property |
| "UniversalMorphismAssociation" | association of morphism names/edges in the abstract product characterizing the universal property |
| "UniversalMorphismNames" | list of names of morphisms in the abstract product characterizing the universal property |
| "UniversalMorphismEdges" | list of directed edges associated to morphisms in the abstract product characterizing the universal property |
| "UniversalMorphismCount" | number of morphisms in the abstract product characterizing the universal property |
| "UniversalReducedMorphismAssociation" | association of morphism names/edges in the abstract product characterizing the universal property, modulo morphism equivalences |
| "UniversalReducedMorphismNames" | list of names of morphisms in the abstract product characterizing the universal property, modulo morphism equivalences |
| "UniversalReducedMorphismEdges" | list of directed edges associated to morphisms in the abstract product characterizing the universal property, modulo morphism equivalences |
| "UniversalReducedMorphismCount" | number of morphisms in the abstract product characterizing the universal property, modulo morphism equivalences |
| "UniversalSimpleMorphismAssociation" | association of morphism names/edges in the abstract product characterizing the universal property, with self-loops and multiedges removed |
| "UniversalSimpleMorphismNames" | list of names of morphisms in the abstract product characterizing the universal property, with self-loops and multiedges removed |
| "UniversalSimpleMorphismEdges" | list of directed edges associated to morphisms in the abstract product characterizing the universal property, with self-loops and multiedges removed |
| "UniversalSimpleMorphismCount" | number of morphisms in the abstract product characterizing the universal property, with self-loops and multiedges removed |
| "UniversalReducedSimpleMorphismAssociation" | association of morphism names/edges in the abstract product characterizing the universal property, with self-loops and multiedges removed, and modulo morphism equivalences |
| "UniversalReducedSimpleMorphismNames" | list of names of morphisms in the abstract product characterizing the universal property, with self-loops and multiedges removed, and modulo morphism equivalences |
| "UniversalReducedSimpleMorphismEdges" | list of directed edges associated to morphisms in the abstract product characterizing the universal property, with self-loops and multiedges removed, and modulo morphism equivalences |
| "UniversalReducedSimpleMorphismCount" | number of morphisms in the abstract product characterizing the universal property, with self-loops and multiedges removed, and modulo morphism equivalences |
| "ProductSymbol" | symbol used to denote products of objects (should be an operator of arbitrary arity) |
| "CompositionSymbol" | symbol used to denote morphism composition (should be a binary operator) |
| "IdentitySymbol" | symbol used to denote identity morphisms (should be a unary operator) |
| "ProductCategory" | abstract category with morphisms representing the abstract product |
| "UniversalProductCategory" | abstract category with morphisms characterizing the universal property of the abstract product |
| "UniversalProductEquations" | list of equations implicitly imposed by the requirement that the universal property of the abstract product is satisfied |
| "FullLabeledGraph" | directed graph form of the abstract product with labels on the morphisms |
| "FullUnlabeledGraph" | directed graph form of the abstract product with no labels on the morphisms |
| "SimpleLabeledGraph" | directed graph form of the abstract product, with self-loops removed, with labels on the morphisms |
| "SimpleUnlabeledGraph" | directed graph form of the abstract product, with self-loops removed, with no labels on the morphisms |
| "UniversalFullLabeledGraph" | directed graph form characterizing the universal property of the abstract product, with labels on the morphisms |
| "UniversalFullUnlabeledGraph" | directed graph form characterizing the universal property of the abstract product, with no labels on the morphisms |
| "UniversalReducedLabeledGraph" | directed graph form characterizing the universal property of the abstract product, modulo morphism equivalences, with labels on the morphisms |
| "UniversalReducedUnlabeledGraph" | directed graph form characterizing the universal property of the abstract product, modulo morphism equivalences, with no labels on the morphisms |
| "UniversalSimpleLabeledGraph" | directed graph form characterizing the universal property of the abstract product, with self-loops and multiedges removed, with labels on the morphisms |
| "UniversalSimpleUnlabeledGraph" | directed graph form characterizing the universal property of the abstract product, with self-loops and multiedges removed, with no labels on the morphisms |
| "UniversalReducedSimpleLabeledGraph" | directed graph form characterizing the universal property of the abstract product, with self-loops and multiedges removed, modulo morphism equivalences, with labels on the morphisms |
| "UniversalReducedSimpleUnlabeledGraph" | directed graph form characterizing the universal property of the abstract product, with self-loops and multiedges removed, modulo morphism equivalences, with no labels on the morphisms |
| "AssociationForm" | abstract product represented as an association of a list of objects, a product symbol, a list of projection morphism names, a composition symbol, an identity symbol, a universal object name, a list of universal morphism names and a unique morphism name |
| "Properties" | list of properties |
Construct a simple abstract product of objects A and B:
| In[1]:= |
| Out[1]= |
Show the full directed graph with labels on the morphisms:
| In[2]:= |
| Out[2]= | 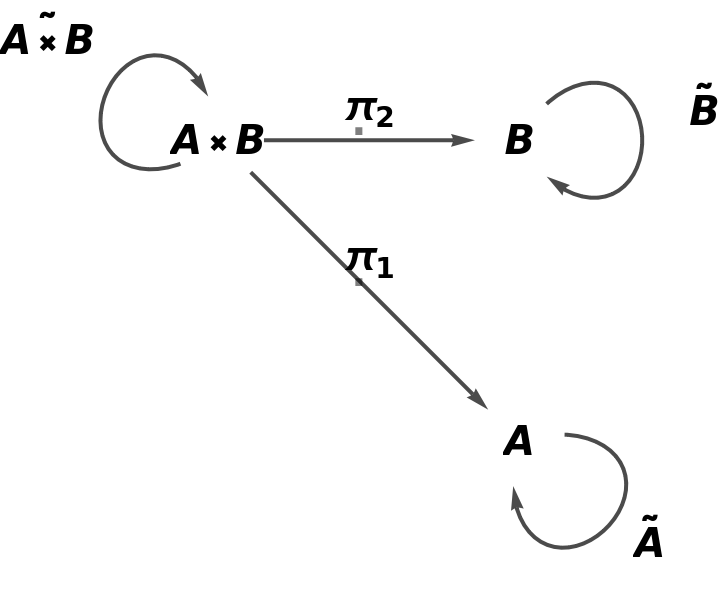 |
Show the full directed graph without labels on the morphisms:
| In[3]:= |
| Out[3]= | 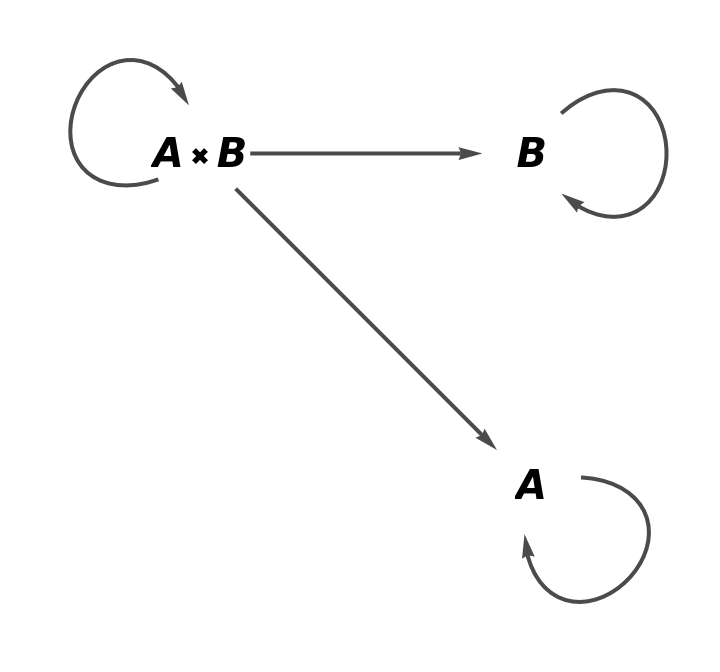 |
Show the full directed graph characterizing the universal property with labels on the morphisms:
| In[4]:= |
| Out[4]= | 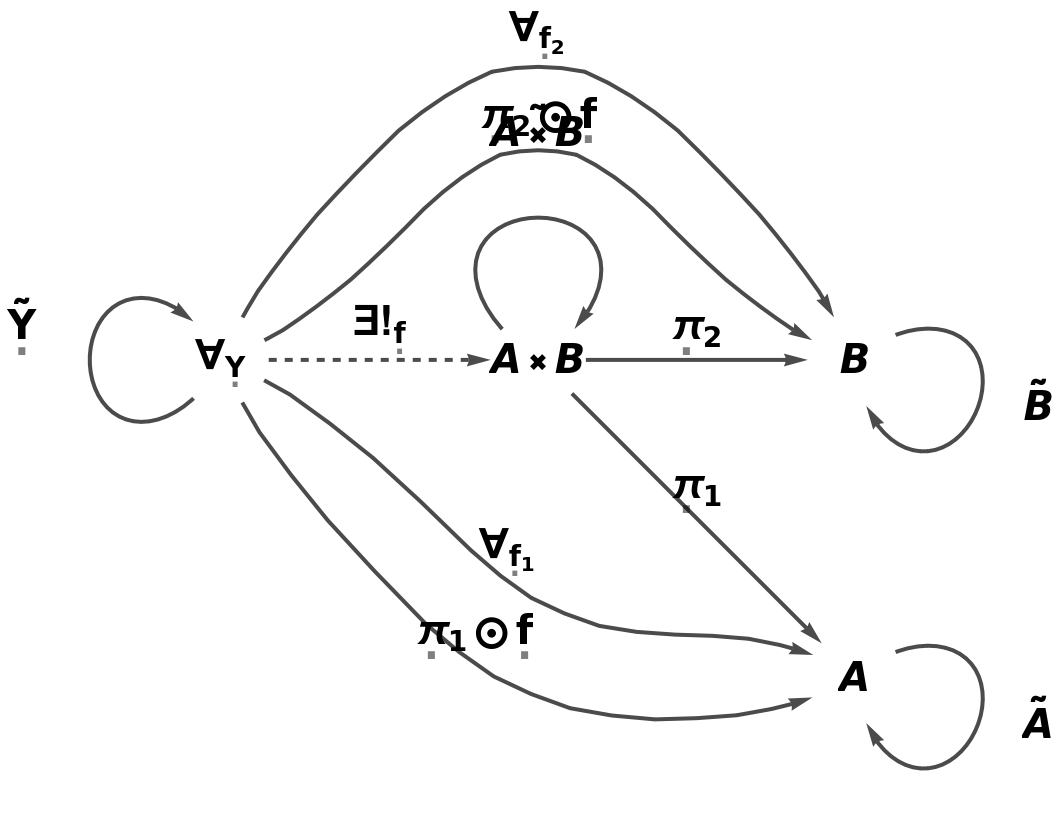 |
Show the full directed graph characterizing the universal property without labels on the morphisms:
| In[5]:= |
| Out[5]= | 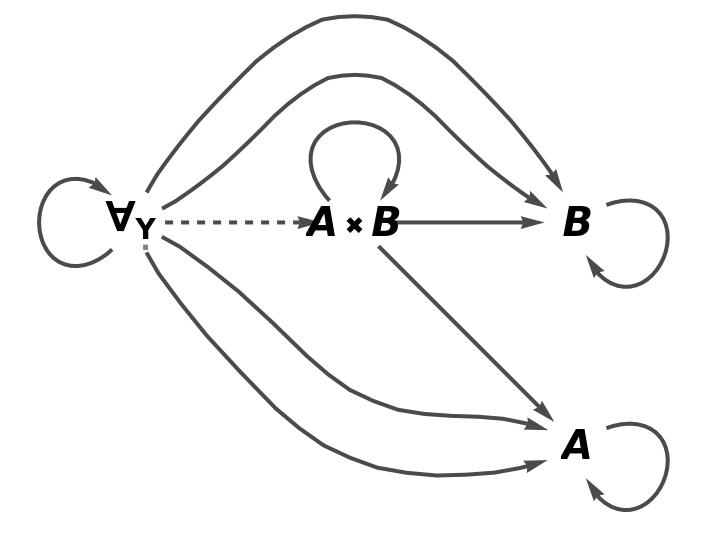 |
Show the Association of morphisms:
| In[6]:= |
| Out[6]= |
Show the Association of (quantified) morphisms characterizing the universal property:
| In[7]:= |
| Out[7]= |
Show the list of directed edges characterizing the universal property:
| In[8]:= |
| Out[8]= |
Show the list of equations characterizing the universal property:
| In[9]:= |
| Out[9]= |
Construct an abstract product of objects U, V and W, but with product symbol ⊗; projection morphisms p1, p2 and p3; and composition and identity symbols ⊕ and ─ and with a universal property characterized by universal object Q; universal morphisms m1, m2 and m3; and unique morphism u:
| In[10]:= |
| Out[10]= |
Show the full directed graph characterizing the universal property with labels on the morphisms:
| In[11]:= |
| Out[11]= | 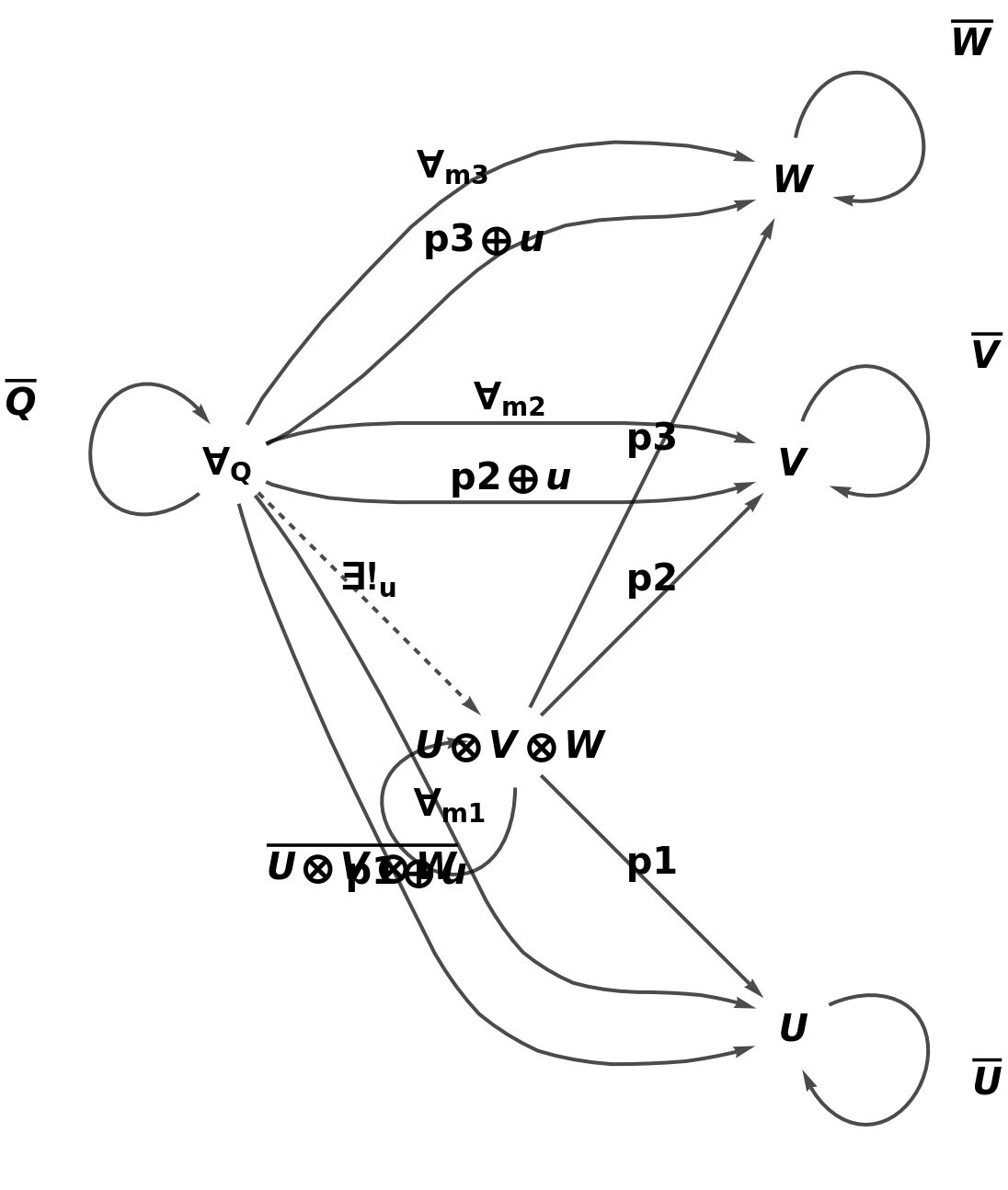 |
Show the full directed graph characterizing the universal property without labels on the morphisms:
| In[12]:= |
| Out[12]= | 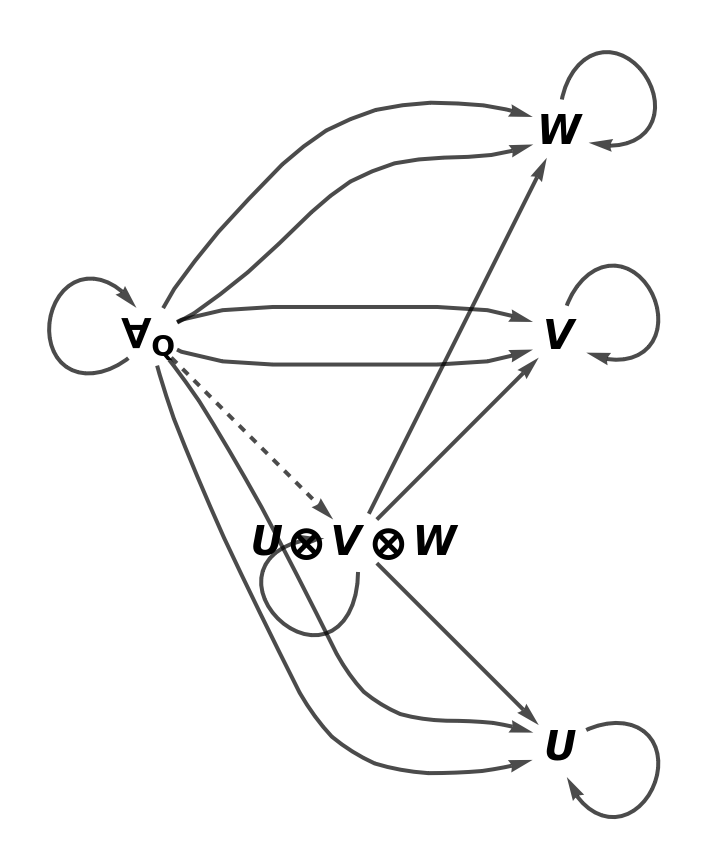 |
Show the reduced directed graph characterizing the universal property with all equivalences between morphisms imposed and with labels on the morphisms:
| In[13]:= |
| Out[13]= | 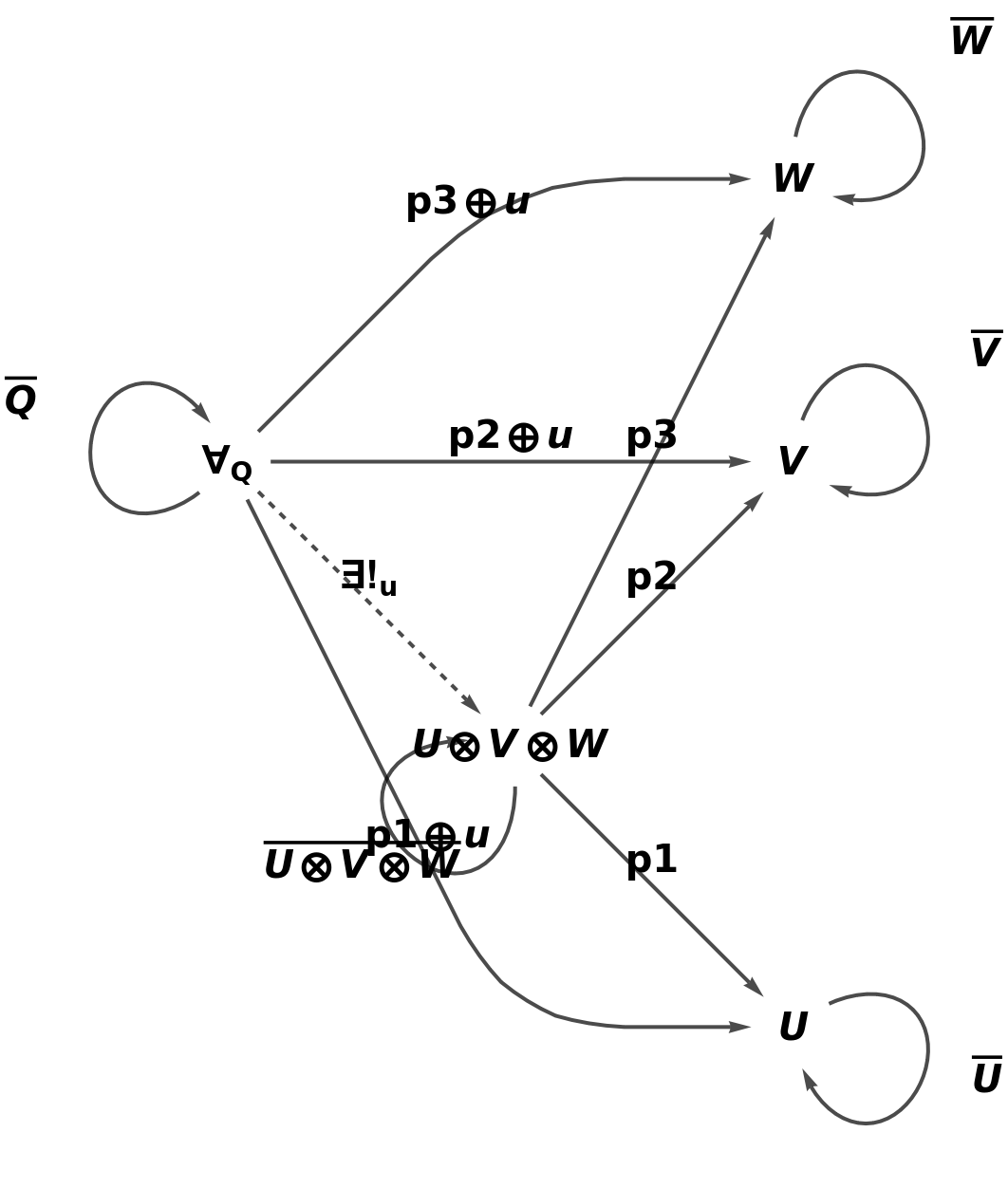 |
Show the reduced directed graph characterizing the universal property without labels on the morphisms:
| In[14]:= |
| Out[14]= | 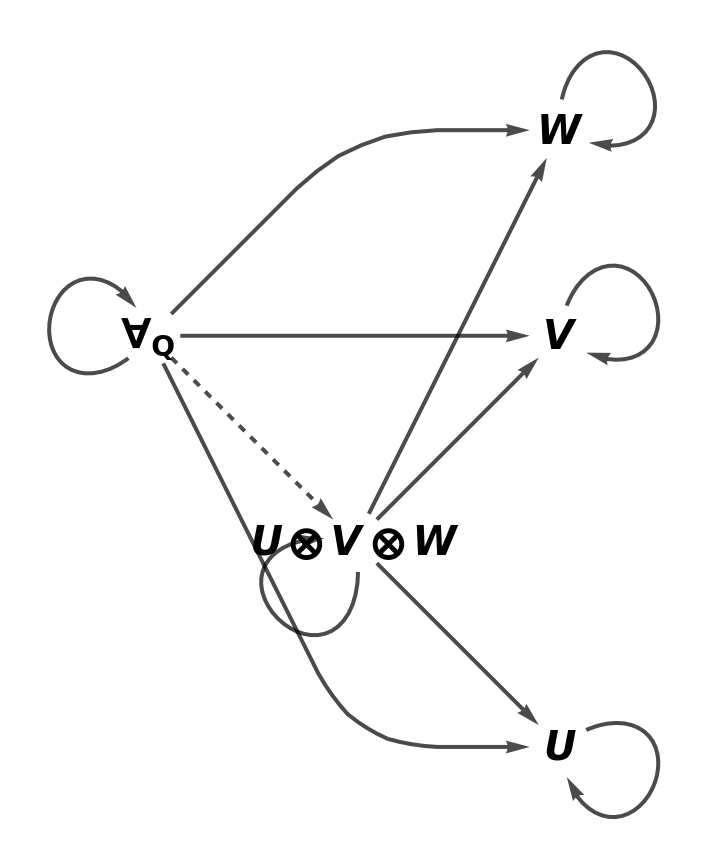 |
Show the Association of morphisms characterizing the universal property with all equivalences between morphisms imposed:
| In[15]:= |
| Out[15]= |
Show the list of equations characterizing the universal property:
| In[16]:= |
| Out[16]= |
Show the association form of the abstract product:
| In[17]:= |
| Out[17]= |  |
Construct an abstract product of objects X and Y:
| In[18]:= |
| Out[18]= |
Construct an abstract category consisting of morphisms to X and Y from some common object Z:
| In[19]:= |
| Out[19]= |
Embed the abstract product into the abstract category (in such a way that the universal property is satisfied):
| In[20]:= |
| Out[20]= |
| In[21]:= |
| Out[21]= | 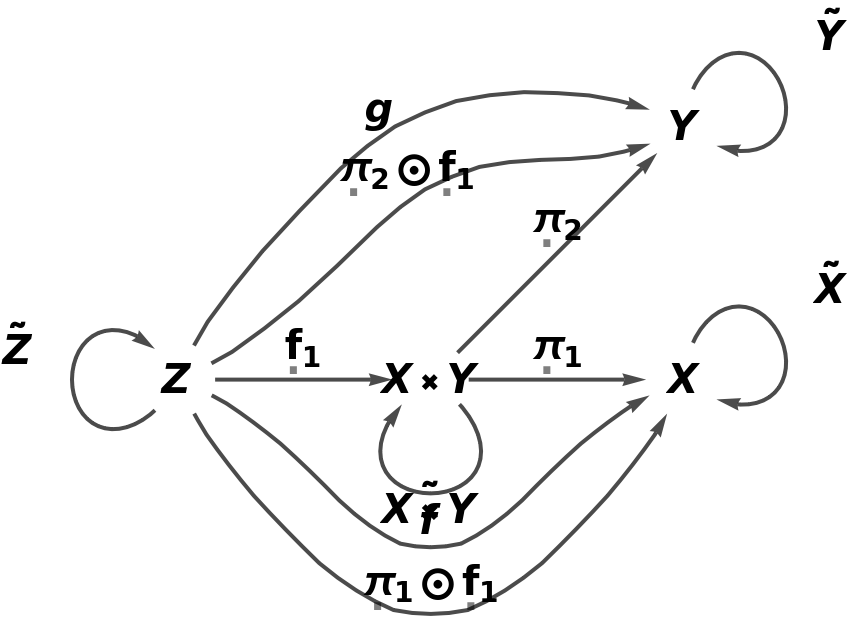 |
Validate that the universal property is indeed satisfied:
| In[22]:= |
| Out[22]= | 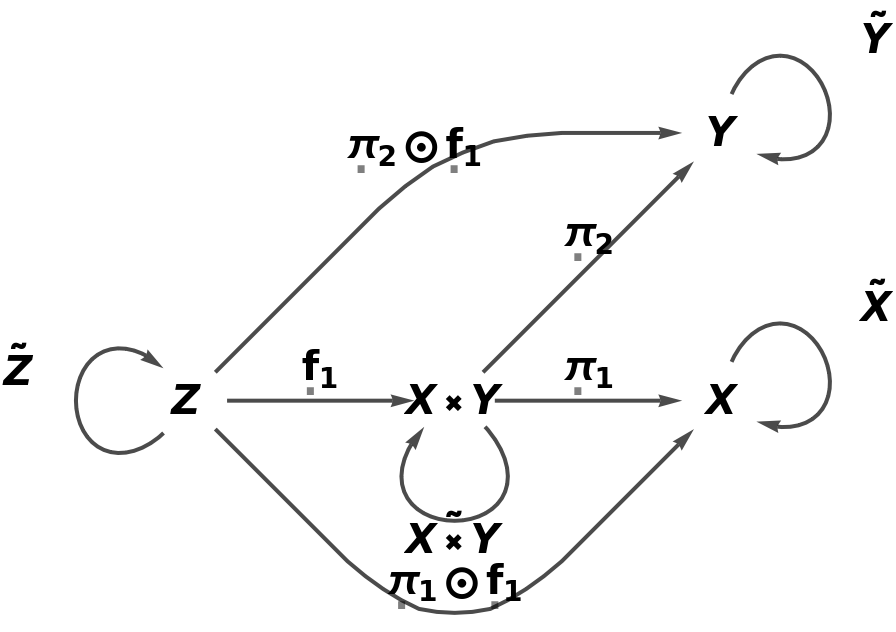 |
| In[23]:= |
| Out[23]= |
Construct a more complicated abstract category consisting of additional morphisms to X and Y from a further common object W:
| In[24]:= |
| Out[24]= |
Embed the abstract product into the more complicated abstract category and validate that the universal property is still satisfied:
| In[25]:= |
| Out[25]= |
| In[26]:= |
| Out[26]= | 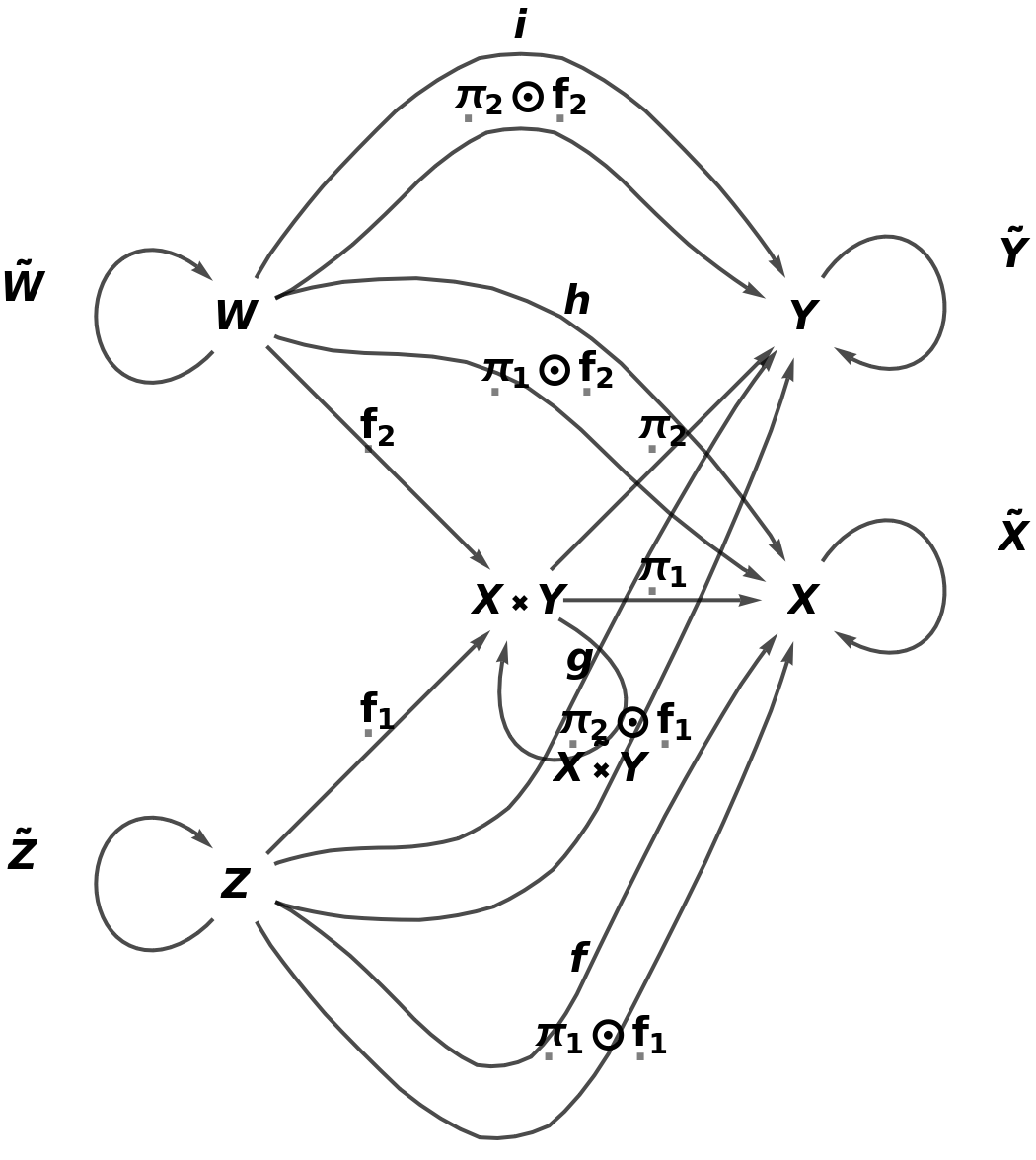 |
| In[27]:= |
| Out[27]= | 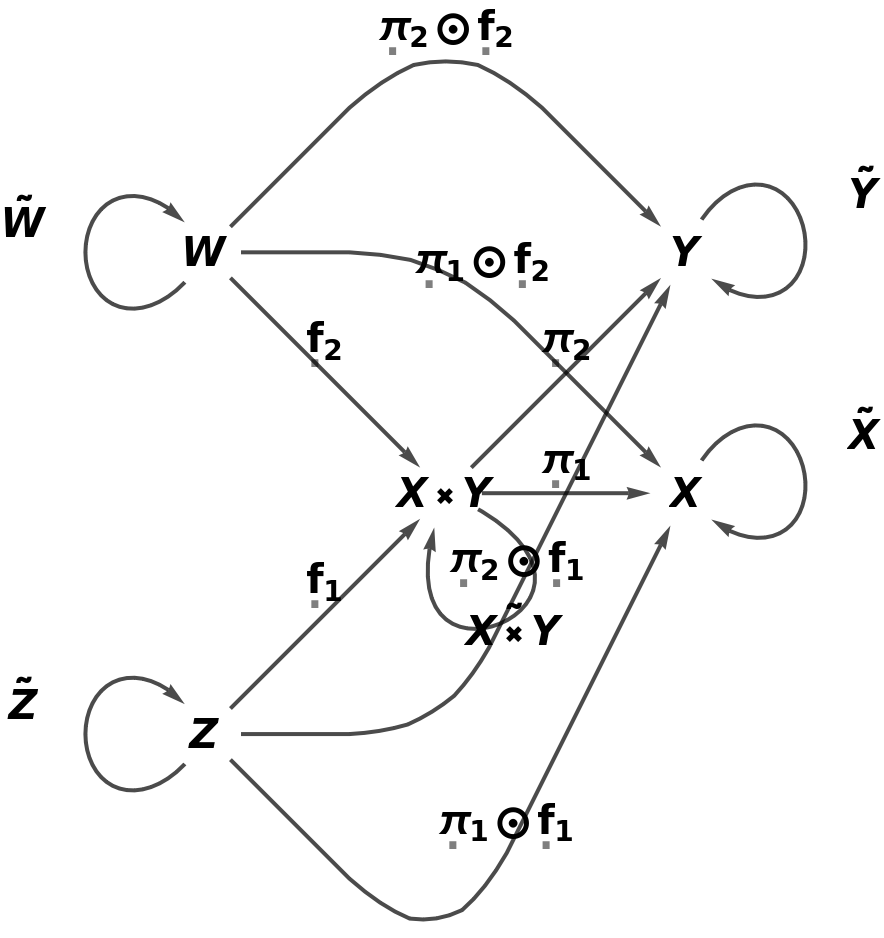 |
| In[28]:= |
| Out[28]= |
Compute minimal abstract category representations of the abstract product and its defining universal property, respectively:
| In[29]:= |
| Out[29]= |
| In[30]:= |
| Out[30]= |
Abstract products can be constructed from a list of objects, a product symbol, a list of names of projection morphisms, a composition symbol and an identity symbol:
| In[31]:= |
| Out[31]= |
| In[32]:= |
| Out[32]= | 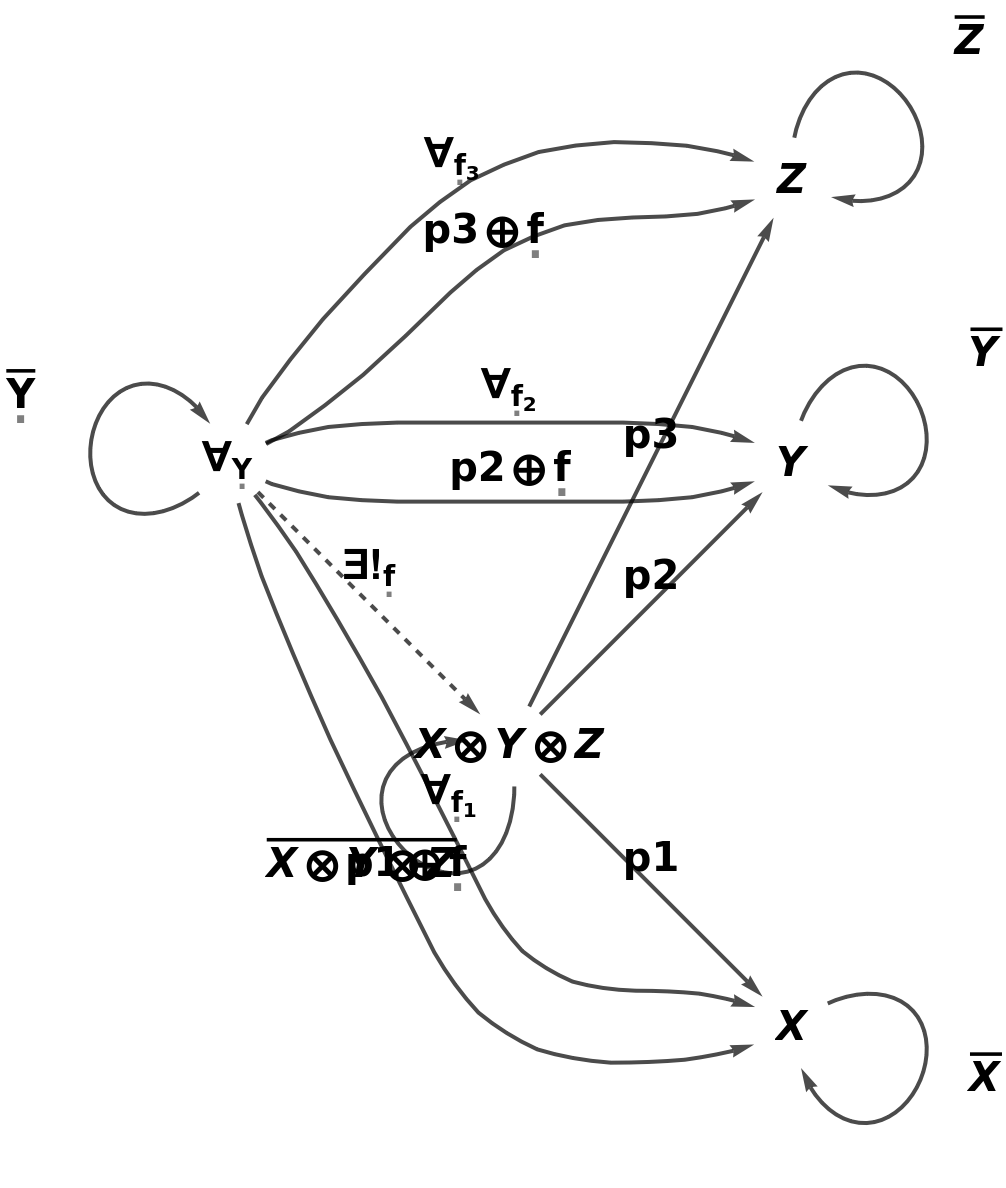 |
A universal object symbol, a list of names of universal morphisms and a unique morphism symbol can also be specified in order to characterize the universal property fully:
| In[33]:= |
| Out[33]= |
| In[34]:= |
| Out[34]= | 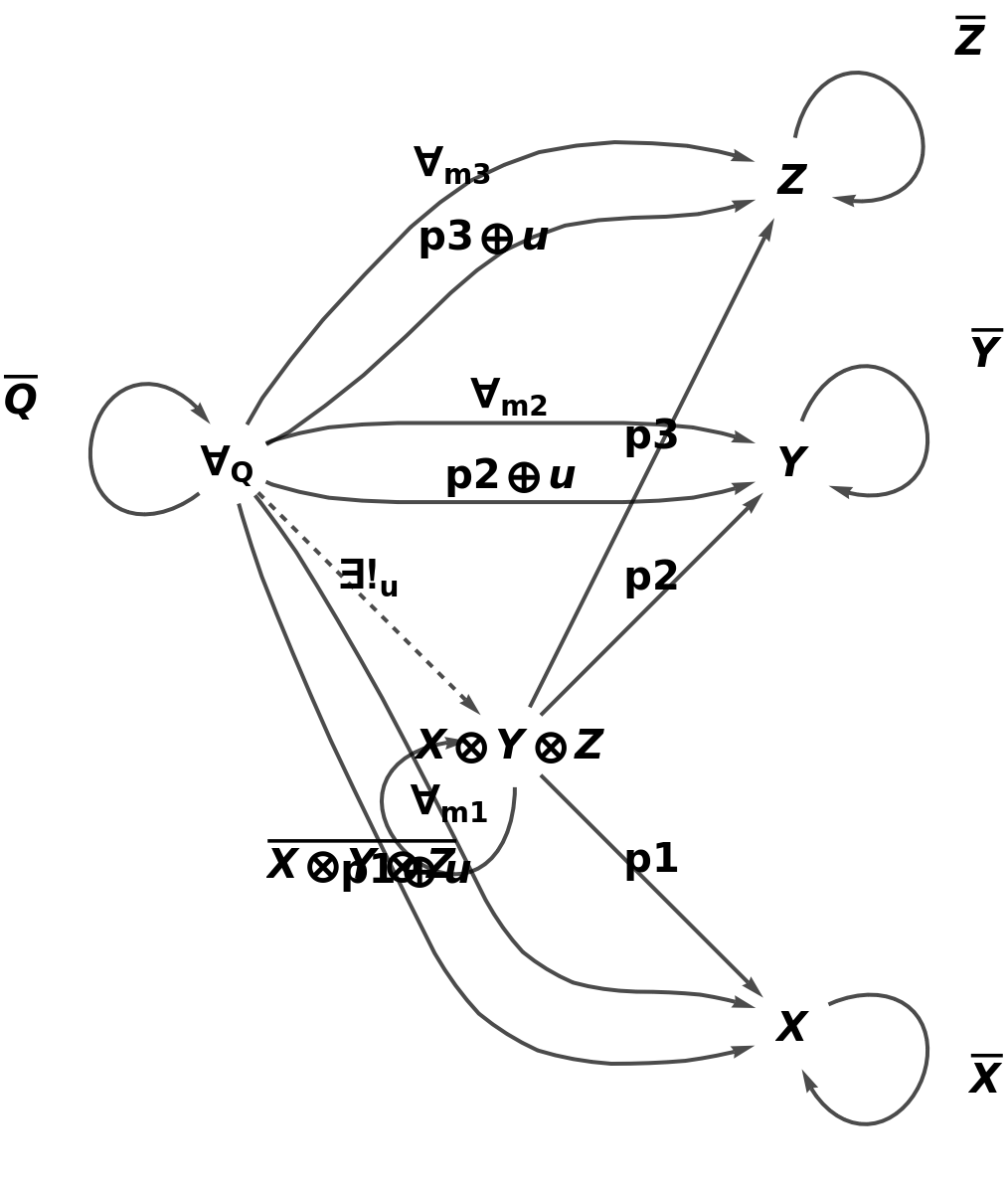 |
Abstract products can also be constructed directly from a list of objects and a list of names of projection morphisms (plus composition and identity symbols):
| In[35]:= |
| Out[35]= |
| In[36]:= |
| Out[36]= | 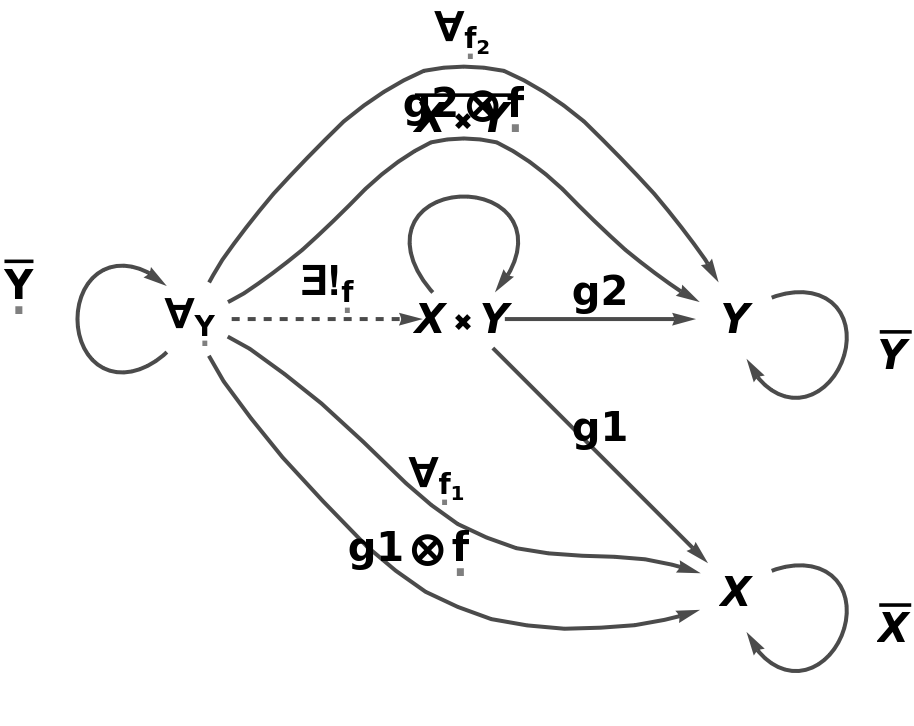 |
Or from an object list with product, composition and identity symbols alone:
| In[37]:= |
| Out[37]= |
| In[38]:= |
| Out[38]= | 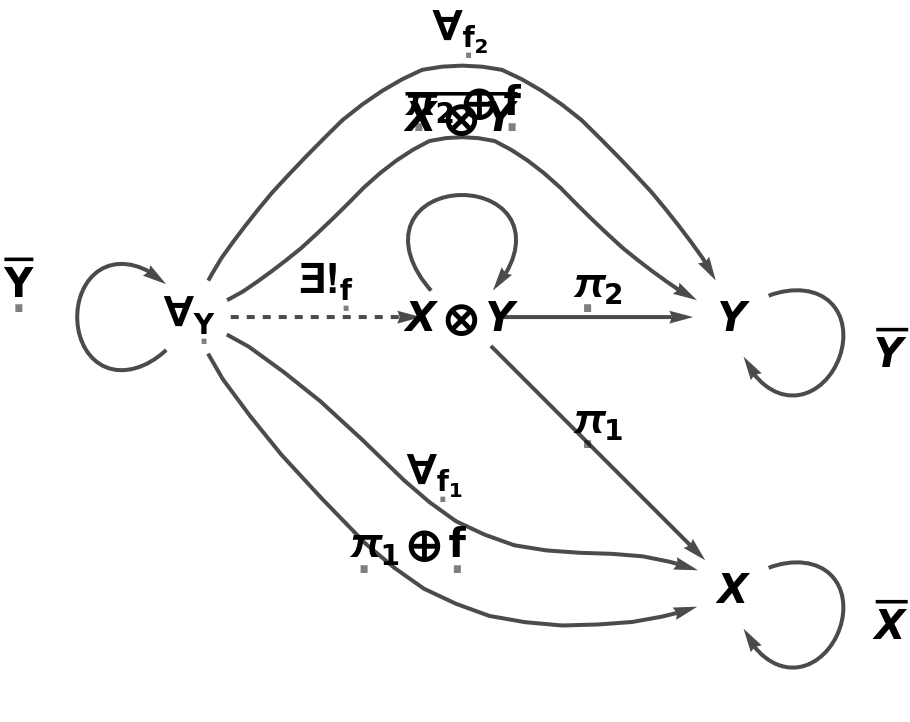 |
If any of these arguments is not explicitly specified, the appropriate defaults are assumed automatically:
| In[39]:= |
| Out[39]= |
| In[40]:= |
| Out[40]= | 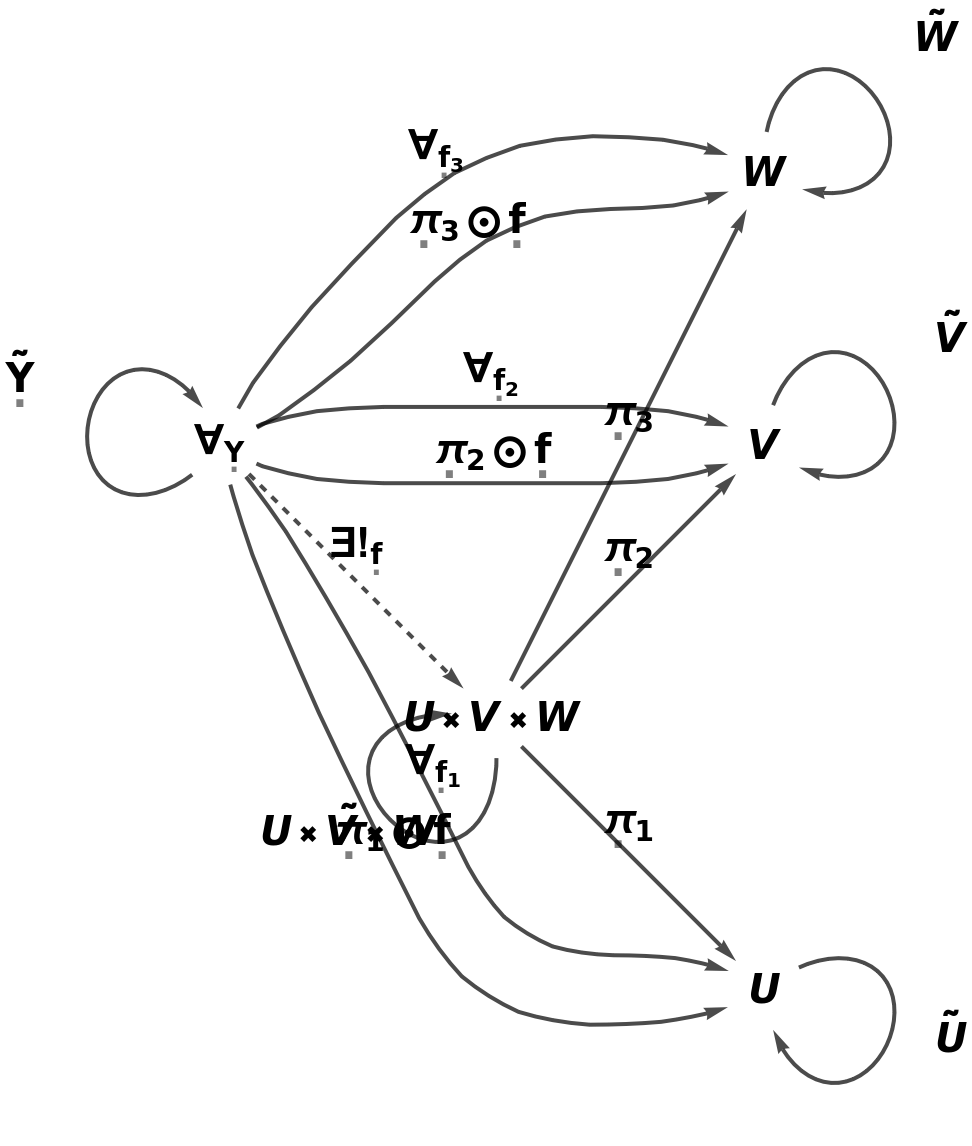 |
New product, composition and identity symbols can be specified for any existing abstract product:
| In[41]:= |
| Out[41]= |
| In[42]:= |
| Out[42]= | 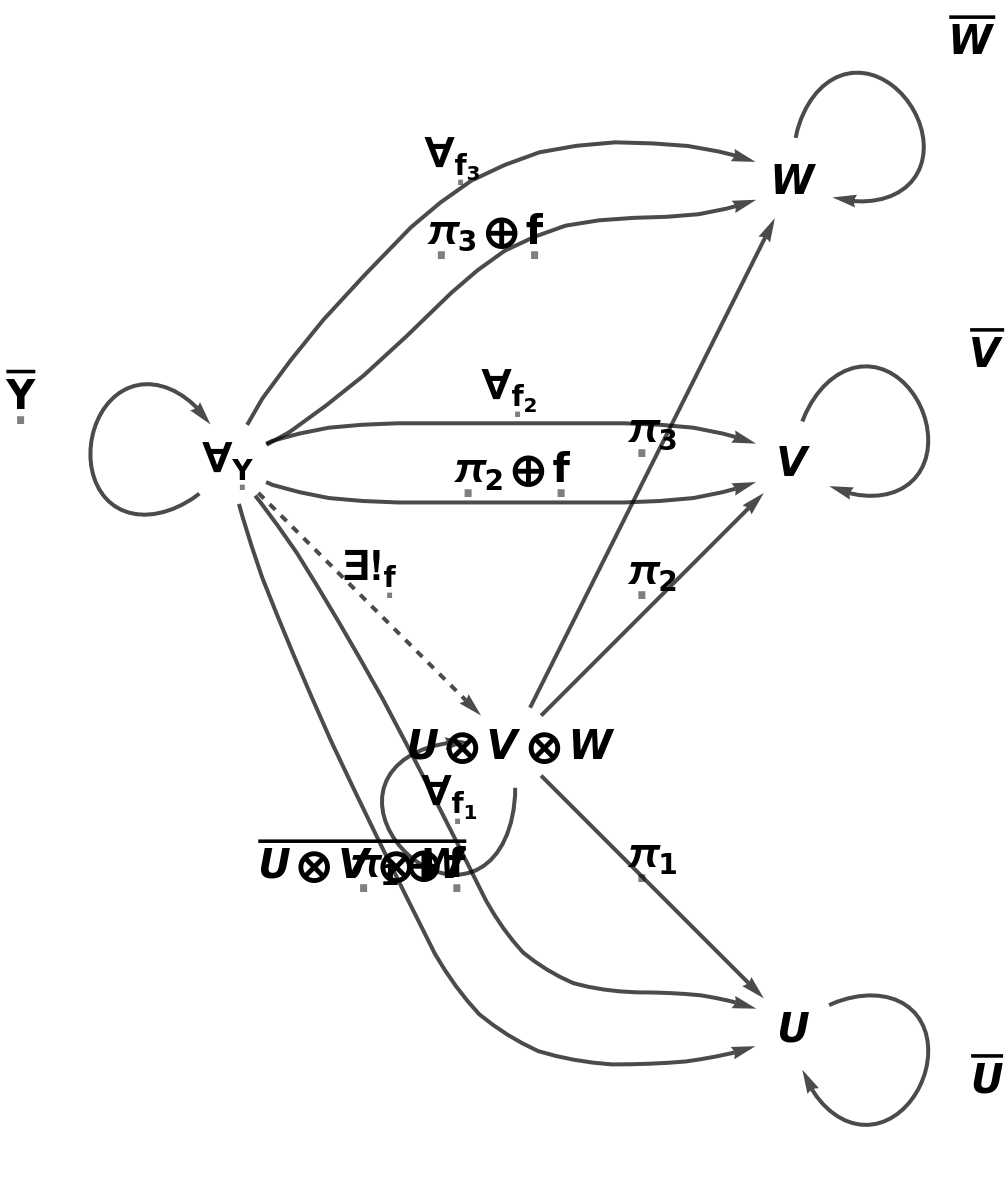 |
From an explicit association:
| In[43]:= | ![ResourceFunction[
"AbstractProduct"][<|"Objects" -> {A, B}, "ProductSymbol" -> CircleTimes, "ProjectionMorphismNames" -> {p1, p2}, "CompositionSymbol" -> CirclePlus, "IdentitySymbol" -> OverBar, "UniversalObjectName" -> Q, "UniversalMorphismNames" -> {f1, f2}, "UniqueMorphismName" -> u|>]](https://www.wolframcloud.com/obj/resourcesystem/images/f59/f59901b2-bab9-4d49-95c1-022617b4b4ec/312bf1ebbe5a6409.png) |
| Out[43]= |
Construct an abstract product of objects X, Y, Z and W:
| In[44]:= |
| Out[44]= |
Show the list of properties:
| In[45]:= |
| Out[45]= |  |
Show the list of objects in the abstract product:
| In[46]:= |
| Out[46]= |
Show the number of objects in the abstract product:
| In[47]:= |
| Out[47]= |
Show the association of morphisms in the abstract product:
| In[48]:= |
| Out[48]= |
Show the list of names of morphisms in the abstract product:
| In[49]:= |
| Out[49]= |
Show the list of directed edges corresponding to morphisms in the abstract product:
| In[50]:= |
| Out[50]= |
Show the number of morphisms in the abstract product:
| In[51]:= |
| Out[51]= |
Show the association of simple morphisms (with all self-loops removed) in the abstract product:
| In[52]:= |
| Out[52]= |
Show the list of names of simple morphisms (with all self-loops removed) in the abstract product:
| In[53]:= |
| Out[53]= |
Show the list of directed edges corresponding to simple morphisms (with all self-loops removed) in the abstract product:
| In[54]:= |
| Out[54]= |
Show the number of simple morphisms (with all self-loops removed) in the abstract product:
| In[55]:= |
| Out[55]= |
Show the list of objects characterizing the universal property of the abstract product:
| In[56]:= |
| Out[56]= |
Show the number of objects characterizing the universal property of the abstract product:
| In[57]:= |
| Out[57]= |
Show the association of morphisms characterizing the universal property of the abstract product:
| In[58]:= |
| Out[58]= | 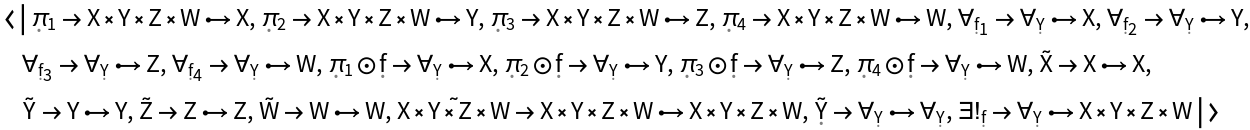 |
Show the list of names of morphisms characterizing the universal property of the abstract product:
| In[59]:= |
| Out[59]= |
Show the list of directed edges corresponding to morphisms characterizing the universal property of the abstract product:
| In[60]:= |
| Out[60]= |
Show the number of morphisms characterizing the universal property of the abstract product:
| In[61]:= |
| Out[61]= |
Show the association of reduced morphisms (modded out by all morphism equivalences) characterizing the universal property of the abstract product:
| In[62]:= |
| Out[62]= | 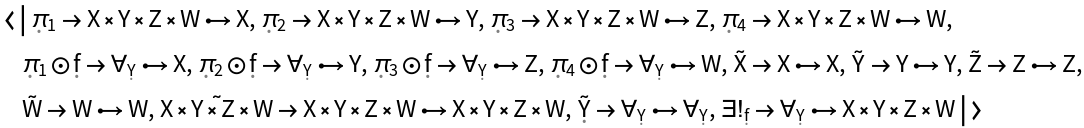 |
Show the list of names of reduced morphisms (modded out by all morphism equivalences) characterizing the universal property of the abstract product:
| In[63]:= |
| Out[63]= |
Show the list of directed edges corresponding to reduced morphisms (modded out by all morphism equivalences) characterizing the universal property of the abstract product:
| In[64]:= |
| Out[64]= |
Show the number of reduced morphisms (modded out by all morphism equivalences) characterizing the universal property of the abstract product:
| In[65]:= |
| Out[65]= |
Show the association of simple morphisms (with all self-loops and multiedges removed) characterizing the universal property of the abstract product:
| In[66]:= |
| Out[66]= |
Show the list of names of simple morphisms (with all self-loops and multiedges removed) characterizing the universal property of the abstract product:
| In[67]:= |
| Out[67]= |
Show the list of directed edges corresponding to simple morphisms (with all self-loops and multiedges removed) characterizing the universal property of the abstract product:
| In[68]:= |
| Out[68]= |
Show the number of simple morphisms (with all self-loops and multiedges removed) characterizing the universal property of the abstract product:
| In[69]:= |
| Out[69]= |
Show the association of reduced simple morphisms (with all self-loops and multiedges removed, plus all morphism equivalences modded out) characterizing the universal property of the abstract product:
| In[70]:= |
| Out[70]= |
Show the list of names of reduced simple morphisms (with all self-loops and multiedges removed, plus all morphism equivalences modded out) characterizing the universal property of the abstract product:
| In[71]:= |
| Out[71]= |
Show the list of directed edges corresponding to reduced simple morphisms (with all self-loops and multiedges removed, plus all morphism equivalences modded out) characterizing the universal property of the abstract product:
| In[72]:= |
| Out[72]= |
Show the number of reduced simple morphisms (with all self-loops and multiedges removed, plus all morphism equivalences modded out) characterizing the universal property of the abstract product:
| In[73]:= |
| Out[73]= |
Show the (arbitrary arity) symbol used to denote the abstract product operation:
| In[74]:= |
| Out[74]= |
Show the (binary) symbol used to denote morphism composition in the abstract product:
| In[75]:= |
| Out[75]= |
Show the (unary) symbol used to denote identity morphisms on objects in the abstract product:
| In[76]:= |
| Out[76]= |
Compute the abstract category whose morphisms represent the abstract product:
| In[77]:= |
| Out[77]= |
Compute the abstract category whose morphisms characterize the universal property of the abstract product:
| In[78]:= |
| Out[78]= |
Show the list of equations imposed implicitly by the requirement that the universal property of the abstract product is satisfied:
| In[79]:= |
| Out[79]= |
Show the full directed graph with labels on the morphisms of the abstract product:
| In[80]:= |
| Out[80]= | 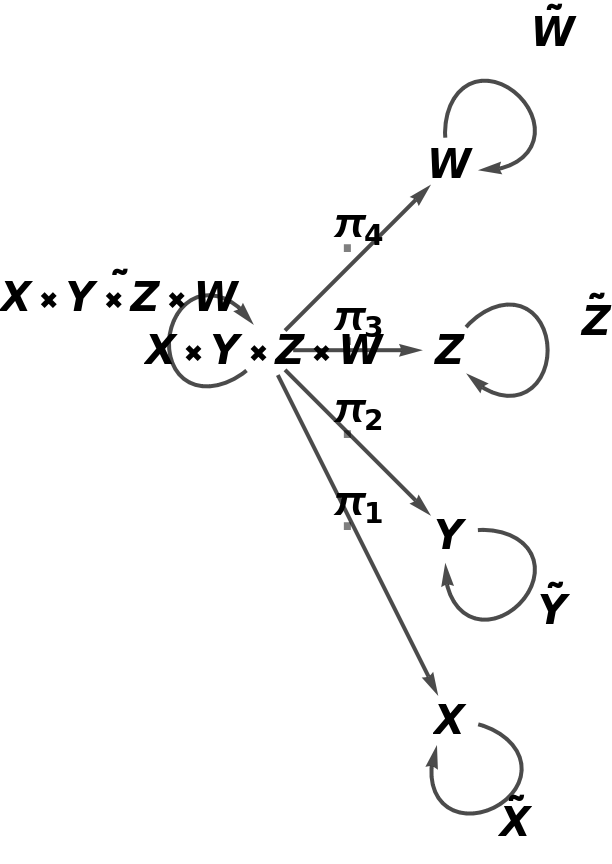 |
Show the full directed graph without labels on the morphisms of the abstract product:
| In[81]:= |
| Out[81]= | 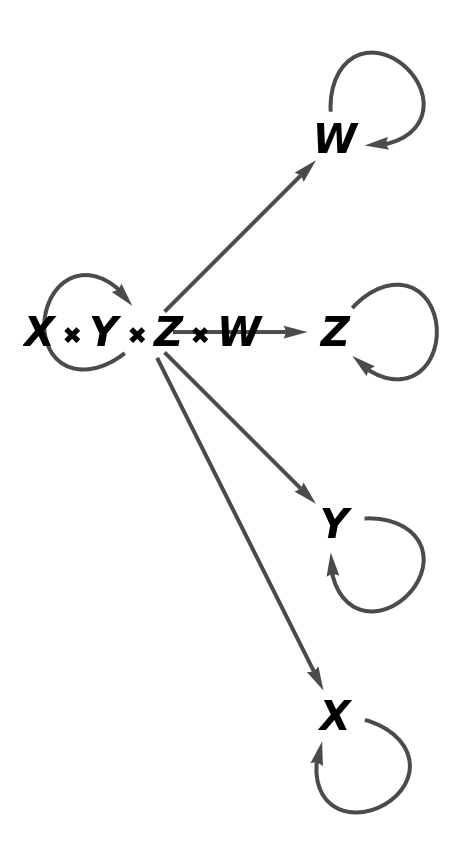 |
Show the simple directed graph with all self-loops removed and with labels on the morphisms of the abstract product:
| In[82]:= |
| Out[82]= | 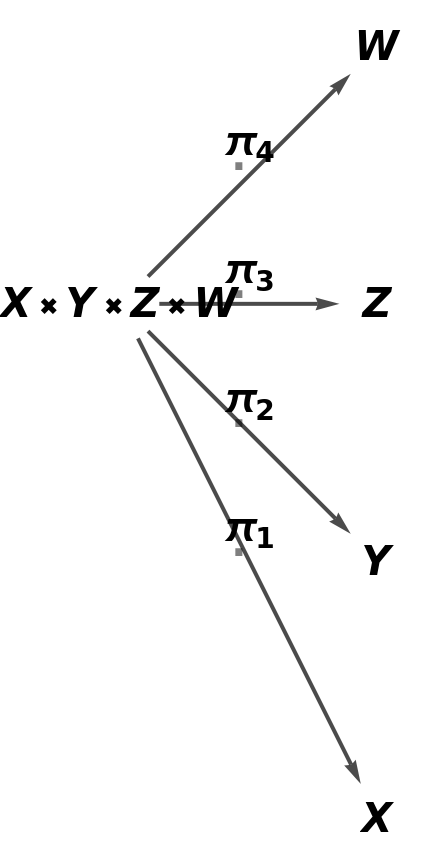 |
Show the simple directed graph with all self-loops removed and without labels on the morphisms of the abstract product:
| In[83]:= |
| Out[83]= | 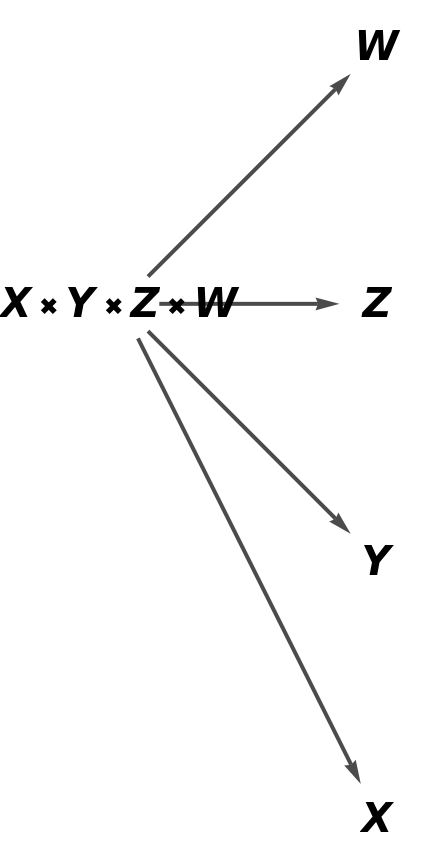 |
Show the full directed graph characterizing the universal property of the abstract product with labels on the morphisms:
| In[84]:= |
| Out[84]= | 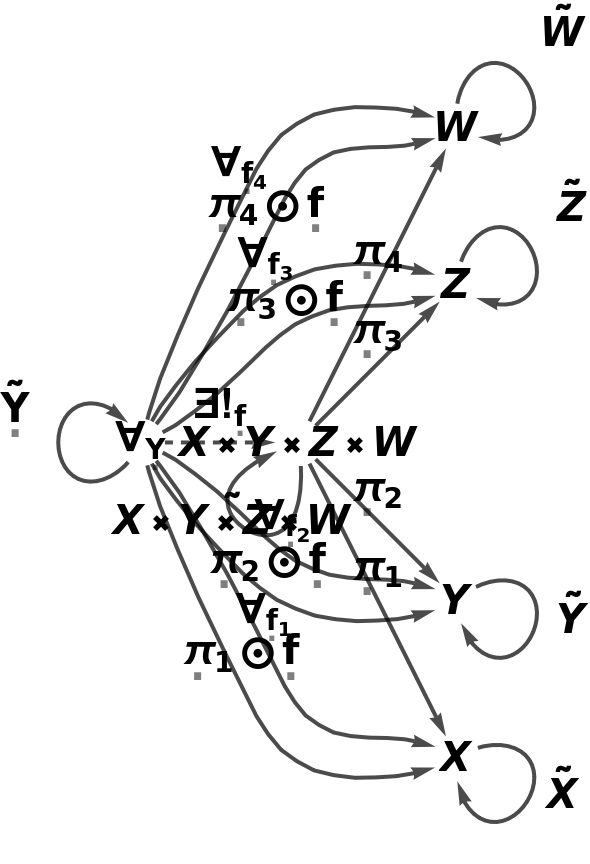 |
Show the full directed graph characterizing the universal property of the abstract product without labels on the morphisms:
| In[85]:= |
| Out[85]= |  |
Show the reduced directed graph characterizing the universal property of the abstract product with all equivalences between morphisms imposed and with labels on the morphisms:
| In[86]:= |
| Out[86]= | 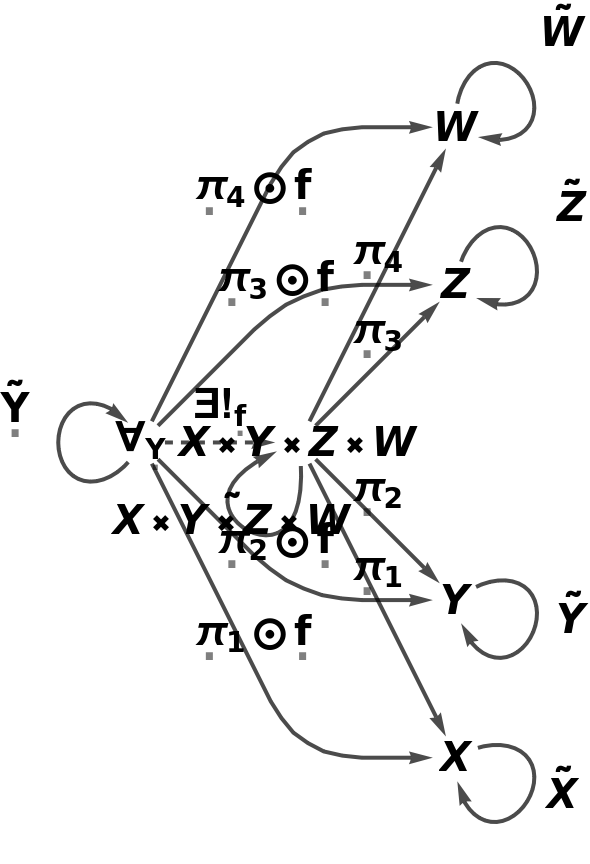 |
Show the reduced directed graph characterizing the universal property of the abstract product with all equivalences between morphisms imposed and without labels on the morphisms:
| In[87]:= |
| Out[87]= | 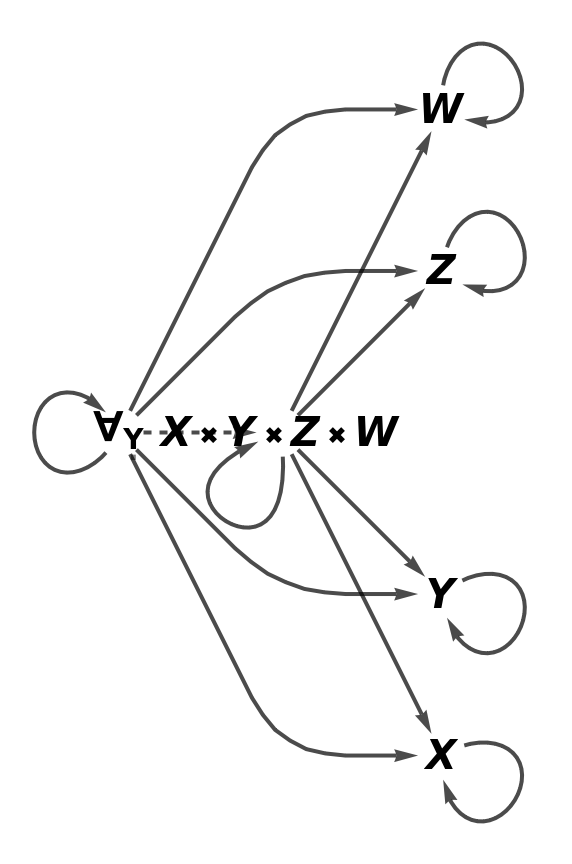 |
Show the simple directed graph characterizing the universal property of the abstract product with all self-loops and multiedges removed and with labels on the morphisms:
| In[88]:= |
| Out[88]= | 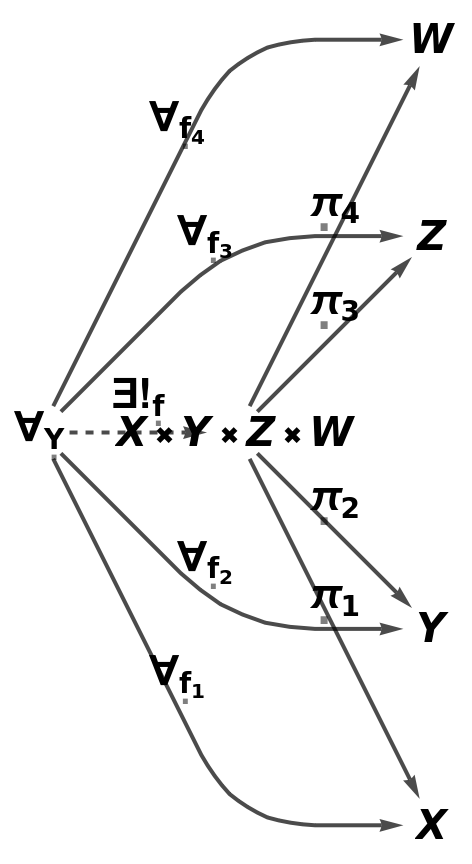 |
Show the simple directed graph characterizing the universal property of the abstract product with all self-loops and multiedges removed and without labels on the morphisms:
| In[89]:= |
| Out[89]= | 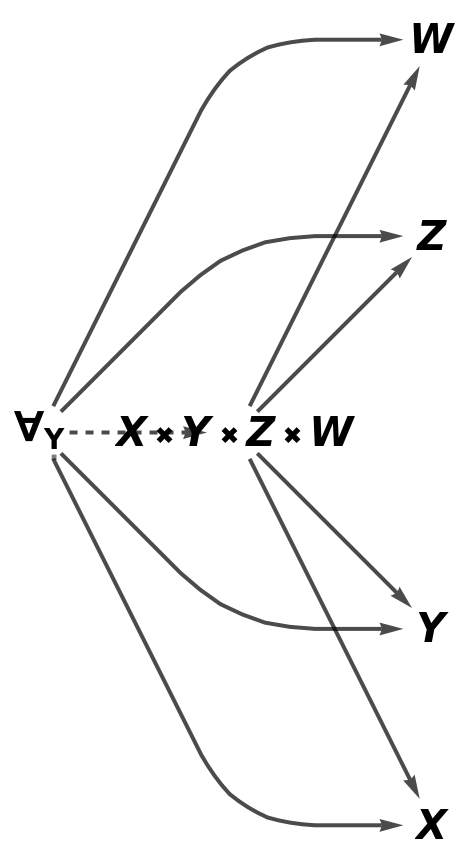 |
Show the reduced simple directed graph characterizing the universal property of the abstract coproduct, with all self-loops and multiedges removed plus all equivalences between morphisms modded out and with labels on the morphisms:
| In[90]:= |
| Out[90]= |  |
Show the reduced simple directed graph characterizing the universal property of the abstract coproduct, with all self-loops and multiedges removed plus all equivalences between morphisms modded out and without labels on the morphisms:
| In[91]:= |
| Out[91]= | 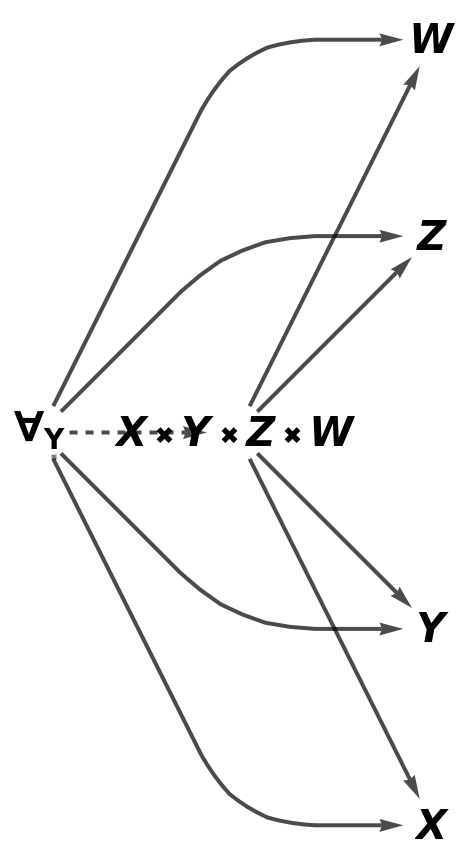 |
Show the explicit association form of the product:
| In[92]:= |
| Out[92]= |  |
This work is licensed under a Creative Commons Attribution 4.0 International License