Wolfram Function Repository
Instant-use add-on functions for the Wolfram Language
Function Repository Resource:
Expand a function into a Thiele continued fraction
ResourceFunction["ThieleExpansion"][f,{x,x0,n}] generates a Thiele continued fraction expansion for f about the point x=x0 up to the nth order convergent, where n is an explicit integer. |
Compute the Thiele continued fraction for the exponential function around x=0:
| In[1]:= |
|
| Out[1]= |

|
Thiele continued fraction of an arbitrary function around x=a:
| In[2]:= |
|
| Out[2]= |
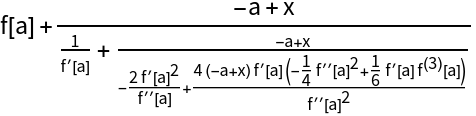
|
Use different methods for generating the Thiele expansion:
| In[3]:= |
|
| Out[3]= |
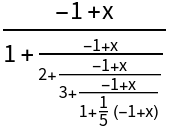
|
| In[4]:= |
|
| Out[4]= |
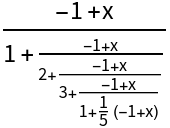
|
The two methods will give results that are mathematically equivalent but may differ in form:
| In[5]:= |
|
| Out[5]= |
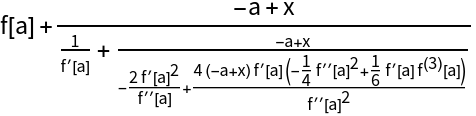
|
| In[6]:= |
|
| Out[6]= |
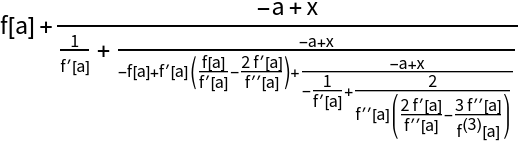
|
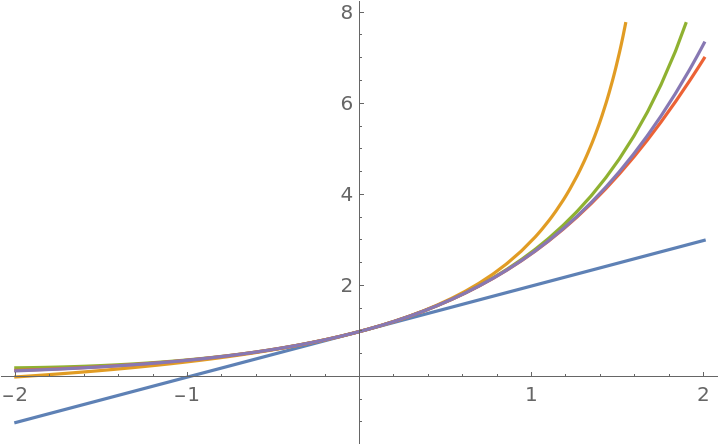
Plot successive Thiele continued fraction approximations to exp(x):
| In[7]:= |
|
| Out[7]= |
|
The Thiele expansion of order n is equivalent to the result of PadeApproximant of order {Ceiling[n/2],Floor[n/2]}:
| In[8]:= |
|
| Out[8]= |
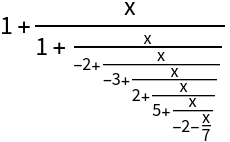
|
| In[9]:= |
|
| Out[9]= |
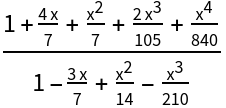
|
| In[10]:= |
|
| Out[10]= |
|
Thiele expansion is not defined for even or odd functions:
| In[11]:= |
|
| Out[11]= |
|
Transform the variable to get a continued fraction expansion:
| In[12]:= |
|
| Out[12]= |
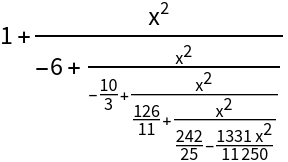
|
This work is licensed under a Creative Commons Attribution 4.0 International License