Wolfram Function Repository
Instant-use add-on functions for the Wolfram Language
Function Repository Resource:
Simulate the evaluation of a formal operator expression as a multiway system
ResourceFunction["MultiwayOperatorSystem"][rules,init,n] generates the results of n steps in the multiway evaluation of a formal operator expression with the specified rules, starting from initial conditions init. | |
ResourceFunction["MultiwayOperatorSystem"][rules,init,n,"prop"] gives the property "prop" for the specified multiway operator expression evaluation. | |
ResourceFunction["MultiwayOperatorSystem"][rules→sel,init,n,…] uses the function sel to select which of the events obtained at each step to include in the evaluation. |
| "Sequential" | applies the first possible replacement (sequential substitution system) |
| "Random" | applies a random replacement |
| {"Random",n} | applies n randomly chosen replacements |
| "AllStatesList" | the list of states generated at each successive step (default) |
| "StatesCountsList" | the number of distinct states generated at each successive step |
| "AllStatesListUnmerged" | the list of all states without any merging |
| "PredecessorRulesList" | the list of states and their corresponding predecessor states at each successive step |
| "EvolutionGraph" | graph formed by the evolution process, with no merging between different time steps |
| "EvolutionGraphStructure" | evolution graph without labeling |
| "EvolutionGraphFull" | graph formed by the evolution process, including equivalent events |
| "EvolutionGraphFullStructure" | full evolution graph without labeling |
| "EvolutionGraphUnmerged" | graph formed by the evolution process, with no merging of equivalent states |
| "EvolutionGraphUnmergedStructure" | unmerged evolution graph without labeling |
| "EvolutionGraphWeighted" | graph formed by the evolution process, with edges weighted by event multiplicity |
| "EvolutionGraphWeightedStructure" | weighted evolution graph without labeling |
| "StatesGraph" | graph of how each distinct state leads to other states |
| "StatesGraphStructure" | states graph without labeling |
| "AllEventsList" | the list of all events that occur at each successive step |
| "EvolutionEventsGraph" | graph showing the evolution process with updating events explicitly included |
| "EvolutionEventsGraphStructure" | evolution events graph without labeling |
| "CausalGraph" | graph of all causal relations between updating events |
| "CausalGraphStructure" | causal graph without labeling |
| "EvolutionCausalGraph" | combined graph of evolution process and causal relationships between events |
| "EvolutionCausalGraphStructure" | evolution causal graph without labeling |
| "CausalGraphInstances" | list of distinct causal graphs for all possible choices of event sequences |
| "CausalGraphStructureInstances" | causal graph instances without labeling |
| "EvolutionCausalGraphInstances" | list of distinct evolution causal graphs for all possible choices of event sequences |
| "EvolutionCausalGraphStructureInstances" | evolution causal graph instances without labeling |
| "BranchPairsList" | list of all branch pairs (i.e. critical pairs) generated in the states graph |
| "NewBranchPairsList" | list of all new branch pairs generated at each successive step |
| "EvolutionBranchPairsList" | list of all branch pairs generated in the evolution graph |
| "NewEvolutionBranchPairsList" | list of all new evolution branch pairs generated at each successive step |
| "BranchPairEventsList" | list of all events yielding branch pairs |
| "NewBranchPairEventsList" | list of all events yielding new branch pairs at each successive step |
| "EvolutionBranchPairEventsList" | list of all events yielding evolution branch pairs |
| "NewEvolutionBranchPairsEventsList" | list of all events yielding new evolution branch pairs at each successive step |
| "BranchialGraph" | graph of branch pair ancestry at a given step |
| "BranchialGraphStructure" | branchial graph without labeling |
| "AllStatesBranchialGraph" | graph of branch pair ancestry across all steps |
| "AllStatesBranchialGraphStructure" | all states branchial graph without labeling |
| "EvolutionBranchialGraph" | graph of evolution branch pair ancestry at a given step |
| "EvolutionBranchialGraphStructure" | evolution branchial graph without labeling |
| "AllStatesEvolutionBranchialGraph" | graph of evolution branch pair ancestry across all steps |
| "AllStatesEvolutionBranchialGraphStructure" | all states evolution branchial graph without labeling |
| "EventBranchialGraph" | graph of branch pair event ancestry at a given time step |
| "EventBranchialGraphStructure" | event branchial graph without labeling |
| "AllEventsBranchialGraph" | graph of branch pair event ancestry across all steps |
| "AllEventsBranchialGraphStructure" | all events branchial graph without labeling |
| "EvolutionEventBranchialGraph" | graph of evolution branch pair event ancestry at a given step |
| "EvolutionEventBranchialGraphStructure" | evolution event branchial graph without labeling |
| "AllEventsEvolutionBranchialGraph" | graph of evolution branch pair event ancestry across all steps |
| "AllEventsEvolutionBranchialGraphStructure" | all events evolution branchial graph without labeling |
| "BranchPairResolutionsList" | association of all resolved and unresolved branch pairs up to a given step |
| "EvolutionBranchPairResolutionsList" | association of all resolved and unresolved evolution branch pairs up to a given step |
| "CausalInvariantQ" | whether the system is causal invariant (all branch pairs converge) |
| "EvolutionCausalInvariantQ" | whether the system is evolution causal invariant (all evolution branch pairs converge) |
| "KnuthBendixCompletion" | list of Knuth–Bendix completion rules required to force causal invariance |
| "EvolutionKnuthBendixCompletion" | list of Knuth–Bendix completion rules required to force evolution causal invariance |
| "StateWeights" | list of weights for all vertices in the states graph |
| "IncludeStepNumber" | False | whether to label states and events with their respective step numbers |
| "IncludeStateID" | False | whether to label states and events with unique IDs |
| "IncludeInitializationEvents" | False | whether to include pseudoevents that set up initial conditions |
| "IncludeEventInstances" | False | whether to show distinct updating events that connect the same states as separate edges |
| "IncludeStateWeights" | False | whether to weight state vertices by their rate of occurrence at a particular time step |
| "IncludeStatePathWeights" | False | whether to weight state vertices by the number of distinct evolution paths that lead to them |
| "StateRenderingFunction" | Automatic | how to label states that appear in graphs |
| "EventRenderingFunction" | Automatic | how to label events that appear in graphs |
| MaxItems | Infinity | how many instances of a causal graph or evolution causal graph to return |
| "GivePredecessors" | False | whether to label branch pairs with their predecessor state |
| "GiveResolvents" | False | whether to label branch pairs with their resolvent state |
| "IncludeSelfPairs" | False | whether to include trivial branch pairs |
| "IncludeFullBranchialSpace" | False | whether to show all possible states in a given branchial graph |
| "LineThickness" | 1 | absolute line thickness for graph edges |
| Inherited | use the explicit vertex name as the label |
| None | use no label for the vertex |
| "shape" | use a shape from the VertexShapeFunction collection |
| func | apply the function func to the name of the vertex |
Show basic multiway operator evaluation for a simple commutative operator system:
| In[1]:= |
|
| Out[1]= |

|
For an operator corresponding to group multiplication:
| In[2]:= |
![ResourceFunction[
"MultiwayOperatorSystem"][{g[x_, g[y_, z_]] :> g[g[x, y], z], g[g[x_, y_], z_] :> g[x, g[y, z]], g[a_, e] :> a, a_ :> g[a, e], g[a_, inv[a_]] :> e, e :> Module[{a = Unique[]}, g[a, inv[a]]]}, g[x, y], 2]](https://www.wolframcloud.com/obj/resourcesystem/images/f40/f404faf7-67a6-4fd2-a0a7-f80eebf7c4df/5b822a7cb8a9a61c.png)
|
| Out[2]= |

|
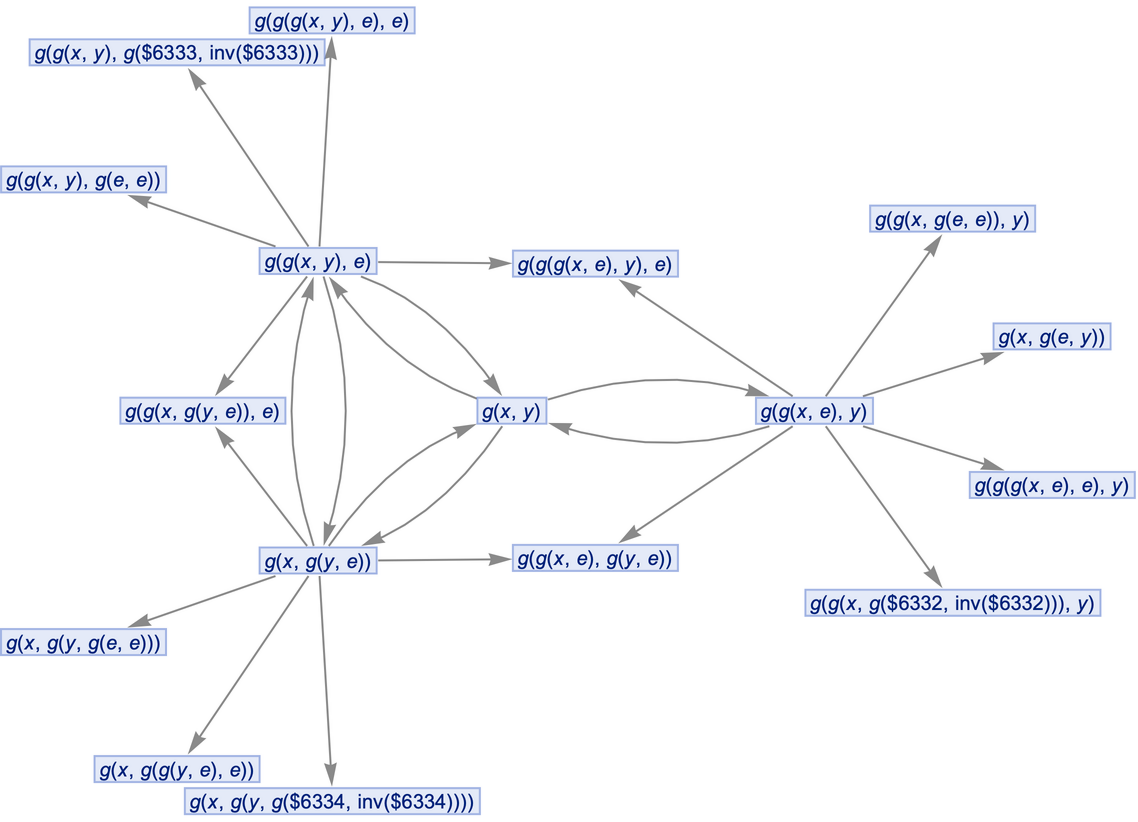
Generate a graph showing how each state is obtained from the others:
| In[3]:= |
![ResourceFunction[
"MultiwayOperatorSystem"][{g[x_, g[y_, z_]] :> g[g[x, y], z], g[g[x_, y_], z_] :> g[x, g[y, z]], g[a_, e] :> a, a_ :> g[a, e], g[a_, inv[a_]] :> e, e :> Module[{a = Unique[]}, g[a, inv[a]]]}, g[x, y], 2, "StatesGraph"]](https://www.wolframcloud.com/obj/resourcesystem/images/f40/f404faf7-67a6-4fd2-a0a7-f80eebf7c4df/1d3f20088f2314df.png)
|
| Out[3]= |
|
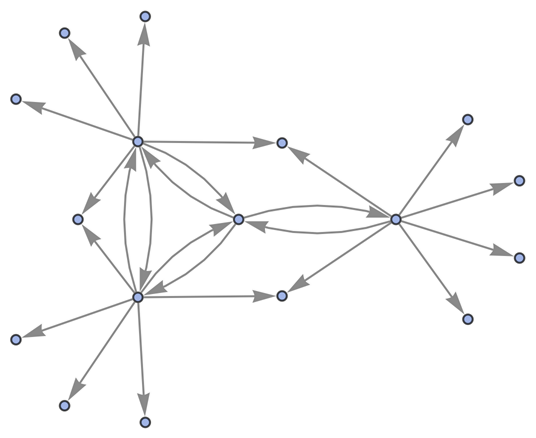
Show the structure of the graph, without labels:
| In[4]:= |
![ResourceFunction[
"MultiwayOperatorSystem"][{g[x_, g[y_, z_]] :> g[g[x, y], z], g[g[x_, y_], z_] :> g[x, g[y, z]], g[a_, e] :> a, a_ :> g[a, e], g[a_, inv[a_]] :> e, e :> Module[{a = Unique[]}, g[a, inv[a]]]}, g[x, y], 2, "StatesGraphStructure"]](https://www.wolframcloud.com/obj/resourcesystem/images/f40/f404faf7-67a6-4fd2-a0a7-f80eebf7c4df/39524fee581a78bd.png)
|
| Out[4]= |
|
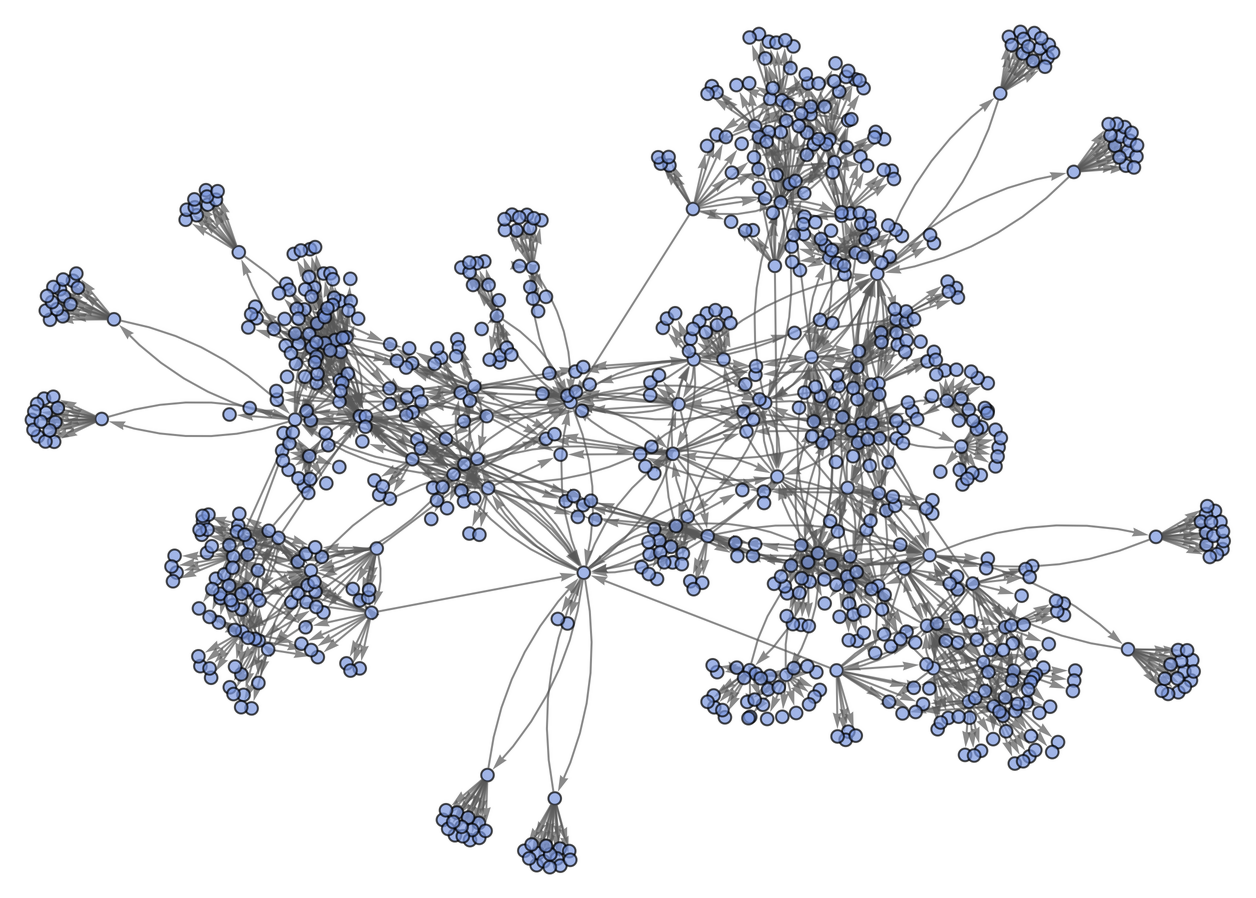
Show four steps without labels:
| In[5]:= |
![ResourceFunction[
"MultiwayOperatorSystem"][{g[x_, g[y_, z_]] :> g[g[x, y], z], g[g[x_, y_], z_] :> g[x, g[y, z]], g[a_, e] :> a, a_ :> g[a, e], g[a_, inv[a_]] :> e, e :> Module[{a = Unique[]}, g[a, inv[a]]]}, g[x, y], 4, "StatesGraphStructure"]](https://www.wolframcloud.com/obj/resourcesystem/images/f40/f404faf7-67a6-4fd2-a0a7-f80eebf7c4df/04da12206c805252.png)
|
| Out[5]= |
|
Generate the list of all updating events applied at each step:
| In[6]:= |
![ResourceFunction[
"MultiwayOperatorSystem"][{g[x_, g[y_, z_]] :> g[g[x, y], z], g[g[x_, y_], z_] :> g[x, g[y, z]], g[a_, e] :> a, a_ :> g[a, e], g[a_, inv[a_]] :> e, e :> Module[{a = Unique[]}, g[a, inv[a]]]}, g[x, y], 2, "AllEventsList"]](https://www.wolframcloud.com/obj/resourcesystem/images/f40/f404faf7-67a6-4fd2-a0a7-f80eebf7c4df/5f71ca0227353668.png)
|
| Out[6]= |
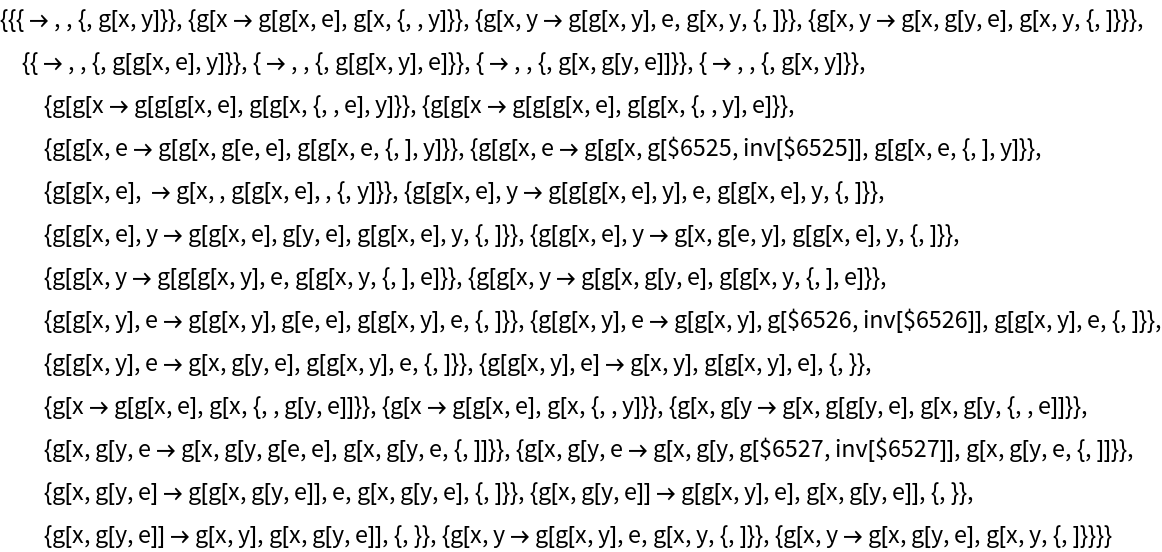
|
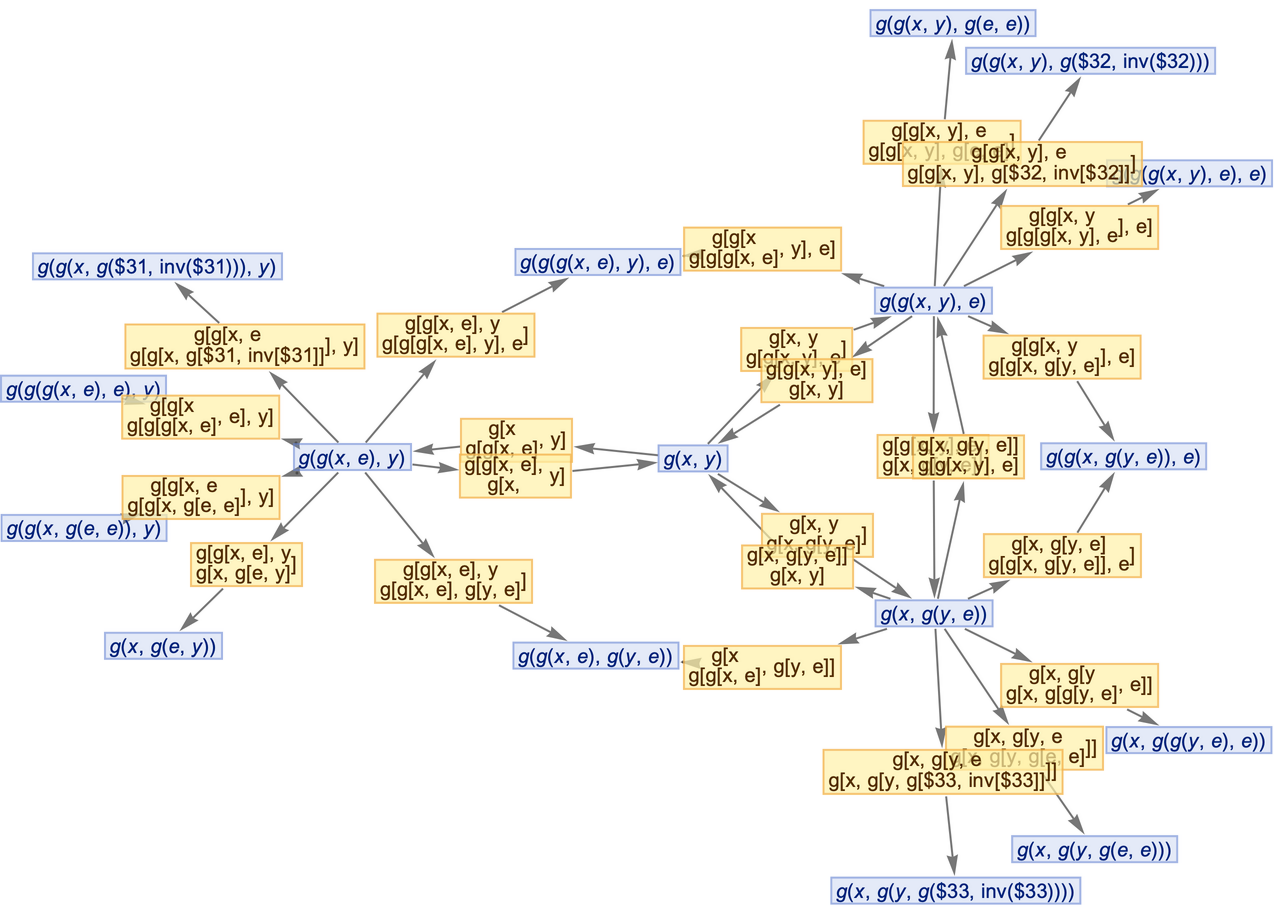
Generate a graph of the evolution history, with updating events included:
| In[7]:= |
![ResourceFunction[
"MultiwayOperatorSystem"][{g[x_, g[y_, z_]] :> g[g[x, y], z], g[g[x_, y_], z_] :> g[x, g[y, z]], g[a_, e] :> a, a_ :> g[a, e], g[a_, inv[a_]] :> e, e :> Module[{a = Unique[]}, g[a, inv[a]]]}, g[x, y], 2, "EvolutionEventsGraph"]](https://www.wolframcloud.com/obj/resourcesystem/images/f40/f404faf7-67a6-4fd2-a0a7-f80eebf7c4df/415fe06c141defde.png)
|
| Out[7]= |
|
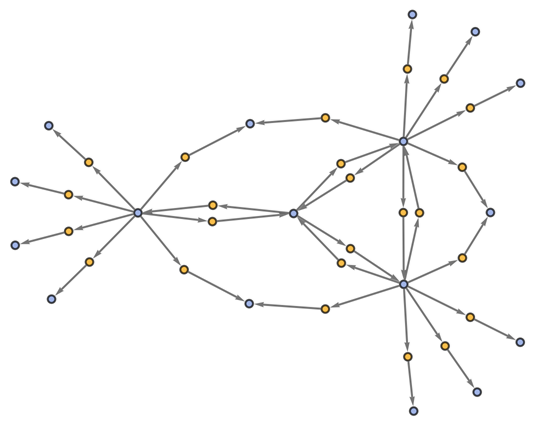
Show the structure of the graph, without labels:
| In[8]:= |
![ResourceFunction[
"MultiwayOperatorSystem"][{g[x_, g[y_, z_]] :> g[g[x, y], z], g[g[x_, y_], z_] :> g[x, g[y, z]], g[a_, e] :> a, a_ :> g[a, e], g[a_, inv[a_]] :> e, e :> Module[{a = Unique[]}, g[a, inv[a]]]}, g[x, y], 2, "EvolutionEventsGraphStructure"]](https://www.wolframcloud.com/obj/resourcesystem/images/f40/f404faf7-67a6-4fd2-a0a7-f80eebf7c4df/6a8b1f23f0278e43.png)
|
| Out[8]= |
|
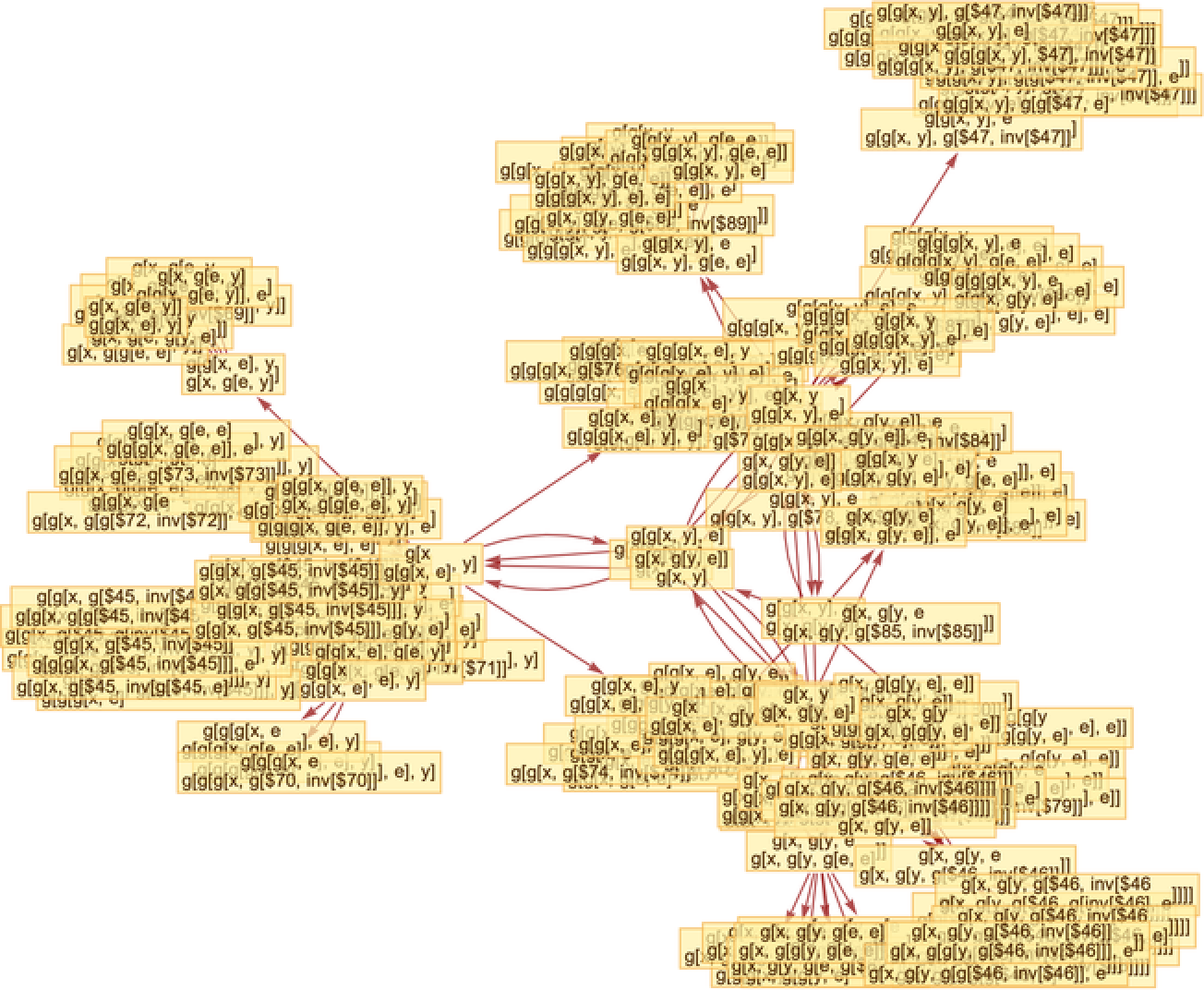
Generate the causal graph, showing dependencies between updating events:
| In[9]:= |
![ResourceFunction[
"MultiwayOperatorSystem"][{g[x_, g[y_, z_]] :> g[g[x, y], z], g[g[x_, y_], z_] :> g[x, g[y, z]], g[a_, e] :> a, a_ :> g[a, e], g[a_, inv[a_]] :> e, e :> Module[{a = Unique[]}, g[a, inv[a]]]}, g[x, y], 3, "CausalGraph"]](https://www.wolframcloud.com/obj/resourcesystem/images/f40/f404faf7-67a6-4fd2-a0a7-f80eebf7c4df/79b7833e5314254f.png)
|
| Out[9]= |
|
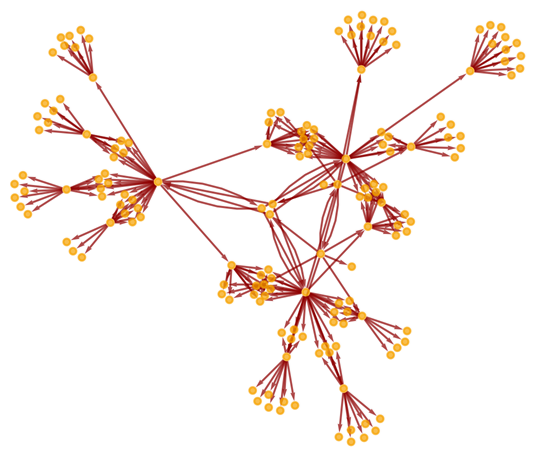
Show the structure of the graph, without labels:
| In[10]:= |
![ResourceFunction[
"MultiwayOperatorSystem"][{g[x_, g[y_, z_]] :> g[g[x, y], z], g[g[x_, y_], z_] :> g[x, g[y, z]], g[a_, e] :> a, a_ :> g[a, e], g[a_, inv[a_]] :> e, e :> Module[{a = Unique[]}, g[a, inv[a]]]}, g[x, y], 3, "CausalGraphStructure"]](https://www.wolframcloud.com/obj/resourcesystem/images/f40/f404faf7-67a6-4fd2-a0a7-f80eebf7c4df/1e72c7d407d9b653.png)
|
| Out[10]= |
|
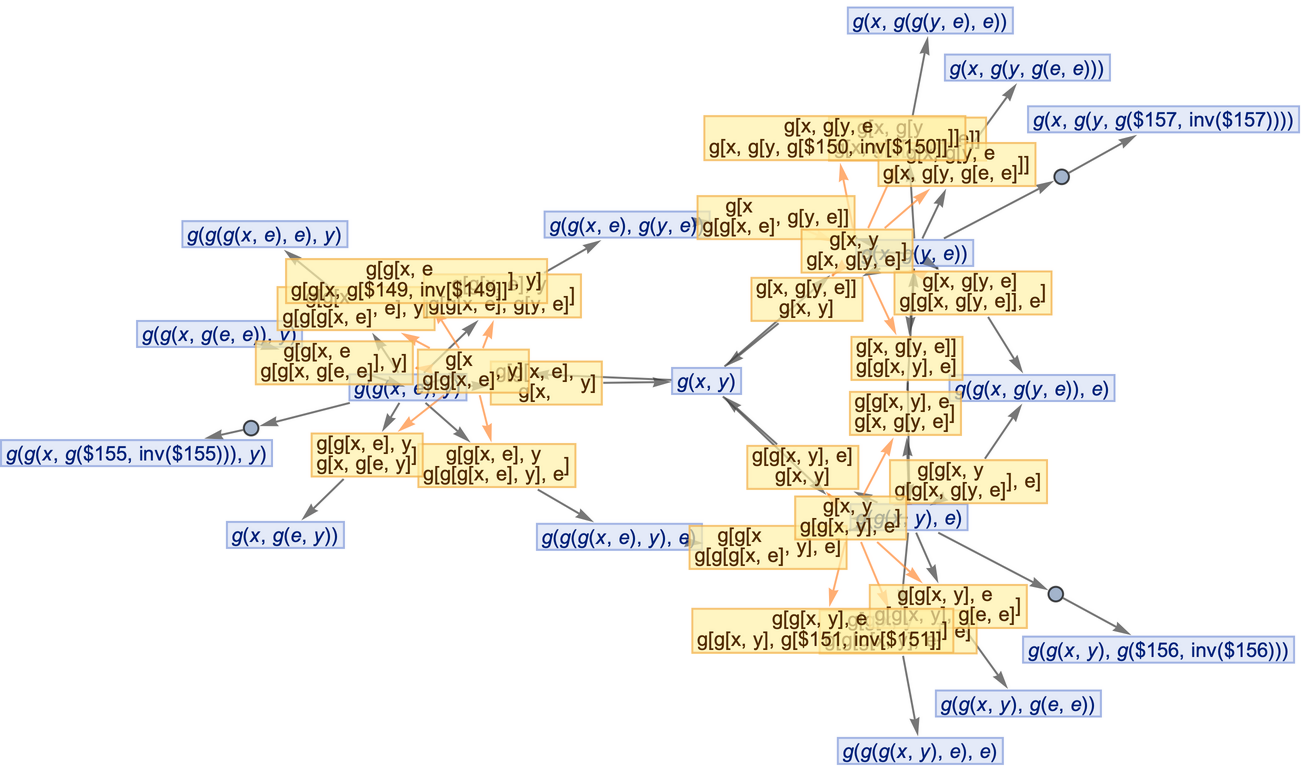
Generate the evolution events graph, with causal connections included:
| In[11]:= |
![ResourceFunction[
"MultiwayOperatorSystem"][{g[x_, g[y_, z_]] :> g[g[x, y], z], g[g[x_, y_], z_] :> g[x, g[y, z]], g[a_, e] :> a, a_ :> g[a, e], g[a_, inv[a_]] :> e, e :> Module[{a = Unique[]}, g[a, inv[a]]]}, g[x, y], 2, "EvolutionCausalGraph"]](https://www.wolframcloud.com/obj/resourcesystem/images/f40/f404faf7-67a6-4fd2-a0a7-f80eebf7c4df/305c6ae531096648.png)
|
| Out[11]= |
|
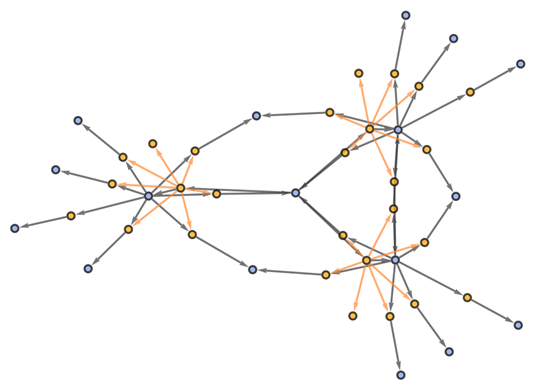
Show the structure of the graph, without labels:
| In[12]:= |
![ResourceFunction[
"MultiwayOperatorSystem"][{g[x_, g[y_, z_]] :> g[g[x, y], z], g[g[x_, y_], z_] :> g[x, g[y, z]], g[a_, e] :> a, a_ :> g[a, e], g[a_, inv[a_]] :> e, e :> Module[{a = Unique[]}, g[a, inv[a]]]}, g[x, y], 2, "EvolutionCausalGraphStructure"]](https://www.wolframcloud.com/obj/resourcesystem/images/f40/f404faf7-67a6-4fd2-a0a7-f80eebf7c4df/446d7982ac6648e0.png)
|
| Out[12]= |
|
Specify an event selection function that picks a random event at each step:
| In[13]:= |
![ResourceFunction[
"MultiwayOperatorSystem"][{g[x_, g[y_, z_]] :> g[g[x, y], z], g[g[x_, y_], z_] :> g[x, g[y, z]], g[a_, e] :> a, a_ :> g[a, e], g[a_, inv[a_]] :> e, e :> Module[{a = Unique[]}, g[a, inv[a]]]} -> "Random", g[x, y], 3, "StatesGraph"]](https://www.wolframcloud.com/obj/resourcesystem/images/f40/f404faf7-67a6-4fd2-a0a7-f80eebf7c4df/7a24527a4b541f91.png)
|
| Out[13]= |
|
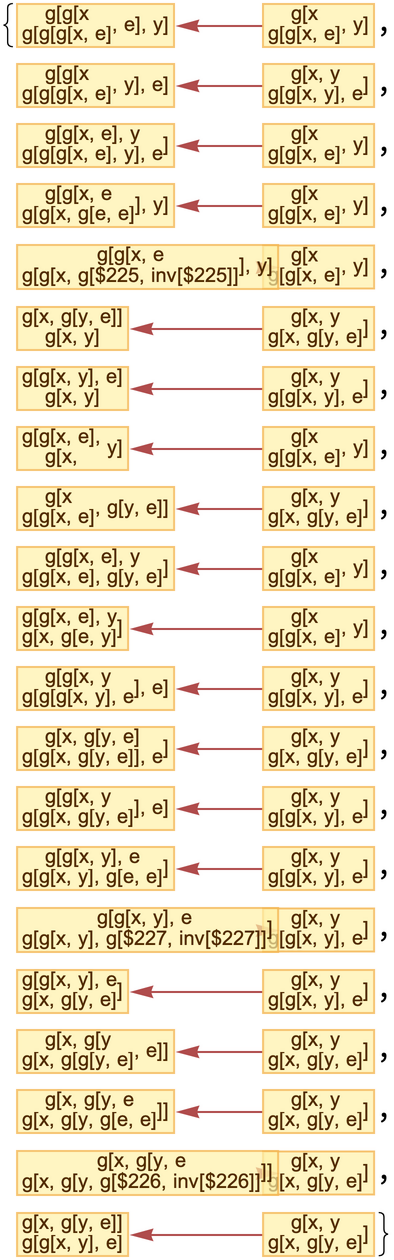
Generate causal graphs for all possible choices of event sequences:
| In[14]:= |
![ResourceFunction[
"MultiwayOperatorSystem"][{g[x_, g[y_, z_]] :> g[g[x, y], z], g[g[x_, y_], z_] :> g[x, g[y, z]], g[a_, e] :> a, a_ :> g[a, e], g[a_, inv[a_]] :> e, e :> Module[{a = Unique[]}, g[a, inv[a]]]}, g[x, y], 2, "CausalGraphInstances"]](https://www.wolframcloud.com/obj/resourcesystem/images/f40/f404faf7-67a6-4fd2-a0a7-f80eebf7c4df/43c7f13dad4d42ea.png)
|
| Out[14]= |
|
Show the structures of the graphs, without labels:
| In[15]:= |
![ResourceFunction[
"MultiwayOperatorSystem"][{g[x_, g[y_, z_]] :> g[g[x, y], z], g[g[x_, y_], z_] :> g[x, g[y, z]], g[a_, e] :> a, a_ :> g[a, e], g[a_, inv[a_]] :> e, e :> Module[{a = Unique[]}, g[a, inv[a]]]}, g[x, y], 2, "CausalGraphStructureInstances"]](https://www.wolframcloud.com/obj/resourcesystem/images/f40/f404faf7-67a6-4fd2-a0a7-f80eebf7c4df/50f94e0c6dbcf7fc.png)
|
| Out[15]= |

|
Generate the list of all branch pairs (i.e. critical pairs):
| In[16]:= |
![ResourceFunction[
"MultiwayOperatorSystem"][{g[x_, g[y_, z_]] :> g[g[x, y], z], g[g[x_, y_], z_] :> g[x, g[y, z]], g[a_, e] :> a, a_ :> g[a, e], g[a_, inv[a_]] :> e, e :> Module[{a = Unique[]}, g[a, inv[a]]]}, e, 2, "BranchPairsList"]](https://www.wolframcloud.com/obj/resourcesystem/images/f40/f404faf7-67a6-4fd2-a0a7-f80eebf7c4df/2a6e97dc306f906d.png)
|
| Out[16]= |

|
Generate the association showing which branch pairs converged and which did not:
| In[17]:= |
![ResourceFunction[
"MultiwayOperatorSystem"][{g[x_, g[y_, z_]] :> g[g[x, y], z], g[g[x_, y_], z_] :> g[x, g[y, z]], g[a_, e] :> a, a_ :> g[a, e], g[a_, inv[a_]] :> e, e :> Module[{a = Unique[]}, g[a, inv[a]]]}, e, 2, "BranchPairResolutionsList"]](https://www.wolframcloud.com/obj/resourcesystem/images/f40/f404faf7-67a6-4fd2-a0a7-f80eebf7c4df/0597665ec128e828.png)
|
| Out[17]= |

|
Prove that group theory is not causal invariant:
| In[18]:= |
![ResourceFunction[
"MultiwayOperatorSystem"][{g[x_, g[y_, z_]] :> g[g[x, y], z], g[g[x_, y_], z_] :> g[x, g[y, z]], g[a_, e] :> a, a_ :> g[a, e], g[a_, inv[a_]] :> e, e :> Module[{a = Unique[]}, g[a, inv[a]]]}, e, 3, "CausalInvariantQ"]](https://www.wolframcloud.com/obj/resourcesystem/images/f40/f404faf7-67a6-4fd2-a0a7-f80eebf7c4df/35a3931f2799f654.png)
|
| Out[18]= |
|
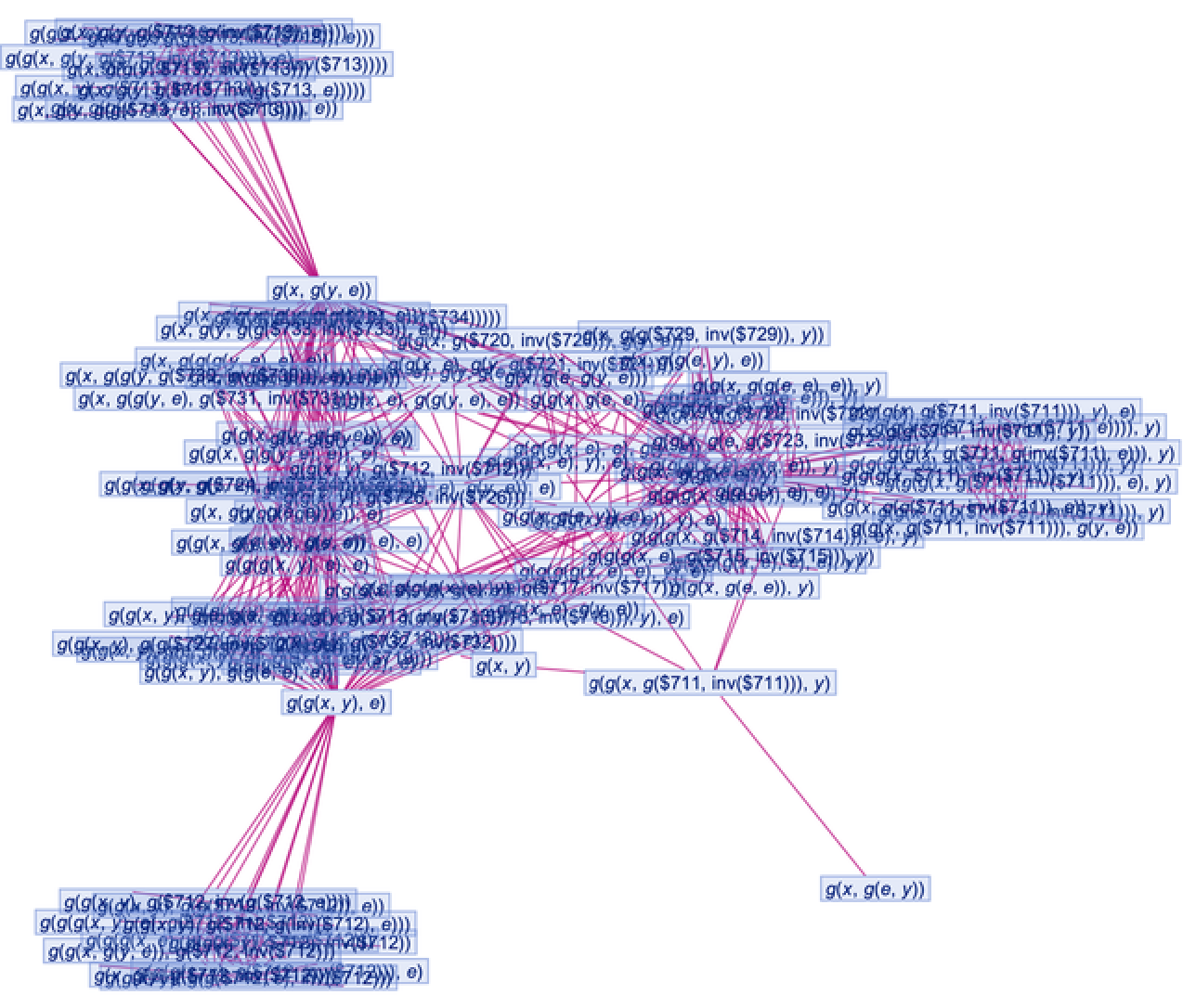
Generate a graph showing branch pair ancestry:
| In[19]:= |
![ResourceFunction[
"MultiwayOperatorSystem"][{g[x_, g[y_, z_]] :> g[g[x, y], z], g[g[x_, y_], z_] :> g[x, g[y, z]], g[a_, e] :> a, a_ :> g[a, e], g[a_, inv[a_]] :> e, e :> Module[{a = Unique[]}, g[a, inv[a]]]}, g[x, y], 3, "BranchialGraph"]](https://www.wolframcloud.com/obj/resourcesystem/images/f40/f404faf7-67a6-4fd2-a0a7-f80eebf7c4df/40b4565f4bf38a43.png)
|
| Out[19]= |
|
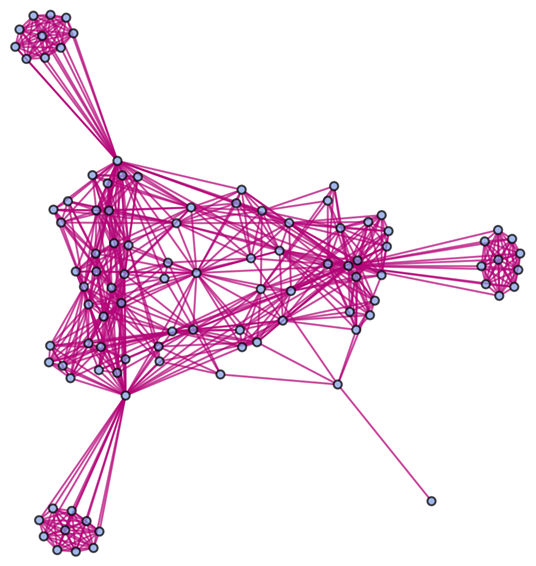
Show the structure of the graph, without labels:
| In[20]:= |
![ResourceFunction[
"MultiwayOperatorSystem"][{g[x_, g[y_, z_]] :> g[g[x, y], z], g[g[x_, y_], z_] :> g[x, g[y, z]], g[a_, e] :> a, a_ :> g[a, e], g[a_, inv[a_]] :> e, e :> Module[{a = Unique[]}, g[a, inv[a]]]}, g[x, y], 3, "BranchialGraphStructure"]](https://www.wolframcloud.com/obj/resourcesystem/images/f40/f404faf7-67a6-4fd2-a0a7-f80eebf7c4df/5b5a8682acf18dd3.png)
|
| Out[20]= |
|
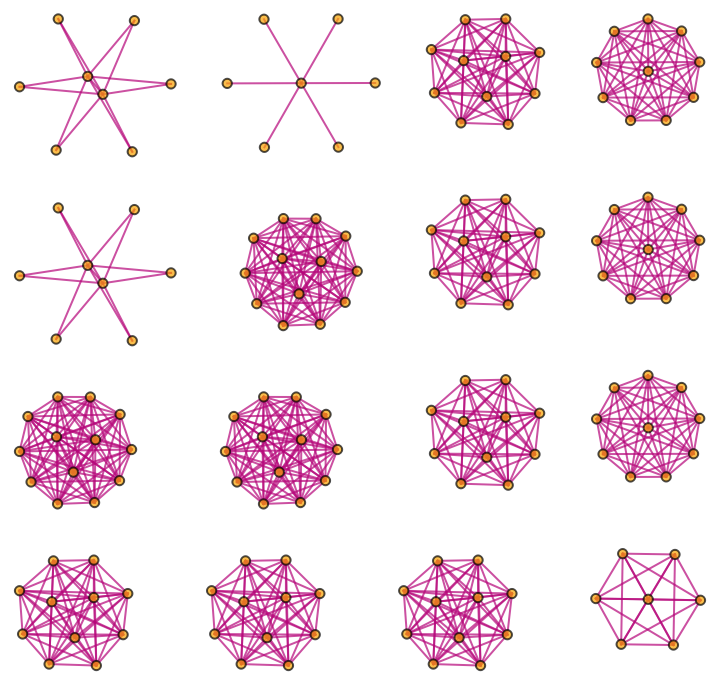
Generate a graph showing branch pair ancestry for the same evaluation:
| In[21]:= |
![ResourceFunction[
"MultiwayOperatorSystem"][{g[x_, g[y_, z_]] :> g[g[x, y], z], g[g[x_, y_], z_] :> g[x, g[y, z]], g[a_, e] :> a, a_ :> g[a, e], g[a_, inv[a_]] :> e, e :> Module[{a = Unique[]}, g[a, inv[a]]]}, g[x, y], 3, "EventBranchialGraphStructure"]](https://www.wolframcloud.com/obj/resourcesystem/images/f40/f404faf7-67a6-4fd2-a0a7-f80eebf7c4df/7fcded1f3cd37555.png)
|
| Out[21]= |
|
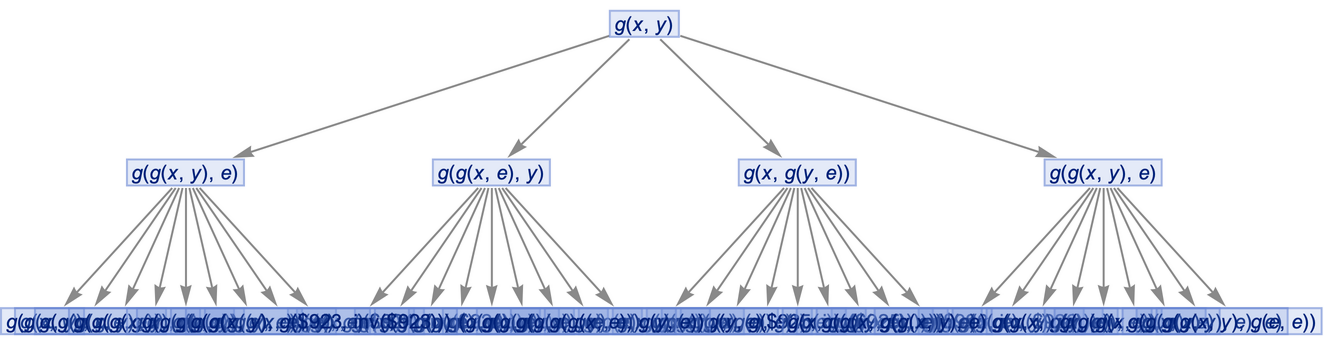
Prevent identical states from being merged by including step numbers and state IDs:
| In[22]:= |
![ResourceFunction[
"MultiwayOperatorSystem"][{g[x_, g[y_, z_]] :> g[g[x, y], z], g[g[x_, y_], z_] :> g[x, g[y, z]], g[a_, e] :> a, a_ :> g[a, e], g[a_, inv[a_]] :> e, e :> Module[{a = Unique[]}, g[a, inv[a]]]}, g[x, y], 2, "StatesGraph", "IncludeStepNumber" -> True, "IncludeStateID" -> True, AspectRatio -> 1/4]](https://www.wolframcloud.com/obj/resourcesystem/images/f40/f404faf7-67a6-4fd2-a0a7-f80eebf7c4df/7789d84593f33665.png)
|
| Out[22]= |
|
List the states:
| In[23]:= |
![ResourceFunction[
"MultiwayOperatorSystem"][{g[x_, g[y_, z_]] :> g[g[x, y], z], g[g[x_, y_], z_] :> g[x, g[y, z]], g[a_, e] :> a, a_ :> g[a, e], g[a_, inv[a_]] :> e, e :> Module[{a = Unique[]}, g[a, inv[a]]]}, g[x, y], 2, "AllStatesList", "IncludeStepNumber" -> True, "IncludeStateID" -> True]](https://www.wolframcloud.com/obj/resourcesystem/images/f40/f404faf7-67a6-4fd2-a0a7-f80eebf7c4df/7ffd039d3acca3fc.png)
|
| Out[23]= |

|
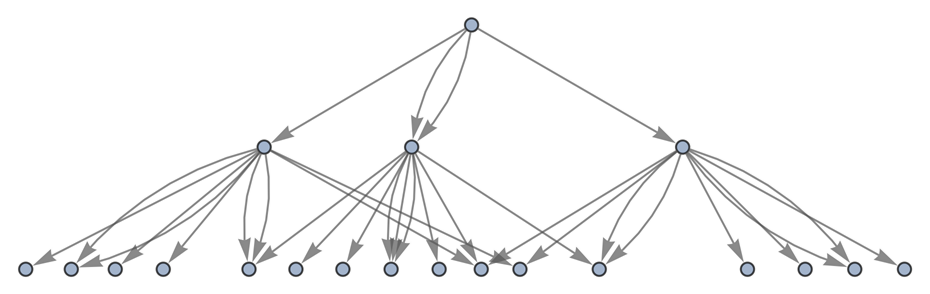
Generate a graph of the full the evolution history, with all events included:
| In[24]:= |
![ResourceFunction[
"MultiwayOperatorSystem"][{g[x_, g[y_, z_]] :> g[g[x, y], z], g[g[x_, y_], z_] :> g[x, g[y, z]], g[a_, e] :> a, a_ :> g[a, e], g[a_, inv[a_]] :> e, e :> Module[{a = Unique[]}, g[a, inv[a]]]}, g[x, y], 2, "EvolutionGraphFullStructure"]](https://www.wolframcloud.com/obj/resourcesystem/images/f40/f404faf7-67a6-4fd2-a0a7-f80eebf7c4df/0ff42da73e61e3e9.png)
|
| Out[24]= |
|
Generate a graph of the full evolution history, with no merging of equivalent states:
| In[25]:= |
![ResourceFunction[
"MultiwayOperatorSystem"][{g[x_, g[y_, z_]] :> g[g[x, y], z], g[g[x_, y_], z_] :> g[x, g[y, z]], g[a_, e] :> a, a_ :> g[a, e], g[a_, inv[a_]] :> e, e :> Module[{a = Unique[]}, g[a, inv[a]]]}, g[x, y], 2, "EvolutionGraphUnmergedStructure"]](https://www.wolframcloud.com/obj/resourcesystem/images/f40/f404faf7-67a6-4fd2-a0a7-f80eebf7c4df/3baee069ae909843.png)
|
| Out[25]= |

|
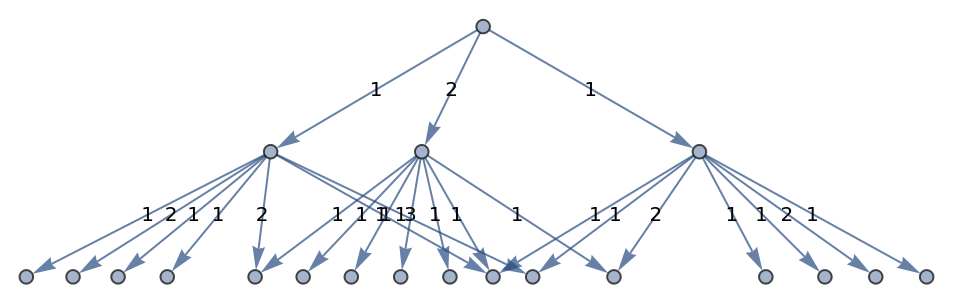
Generate a graph of evolution history, with edges weighted by event multiplicity:
| In[26]:= |
![ResourceFunction[
"MultiwayOperatorSystem"][{g[x_, g[y_, z_]] :> g[g[x, y], z], g[g[x_, y_], z_] :> g[x, g[y, z]], g[a_, e] :> a, a_ :> g[a, e], g[a_, inv[a_]] :> e, e :> Module[{a = Unique[]}, g[a, inv[a]]]}, g[x, y], 2, "EvolutionGraphWeightedStructure", EdgeLabels -> "EdgeWeight"]](https://www.wolframcloud.com/obj/resourcesystem/images/f40/f404faf7-67a6-4fd2-a0a7-f80eebf7c4df/4bc12d9f96433d0a.png)
|
| Out[26]= |
|
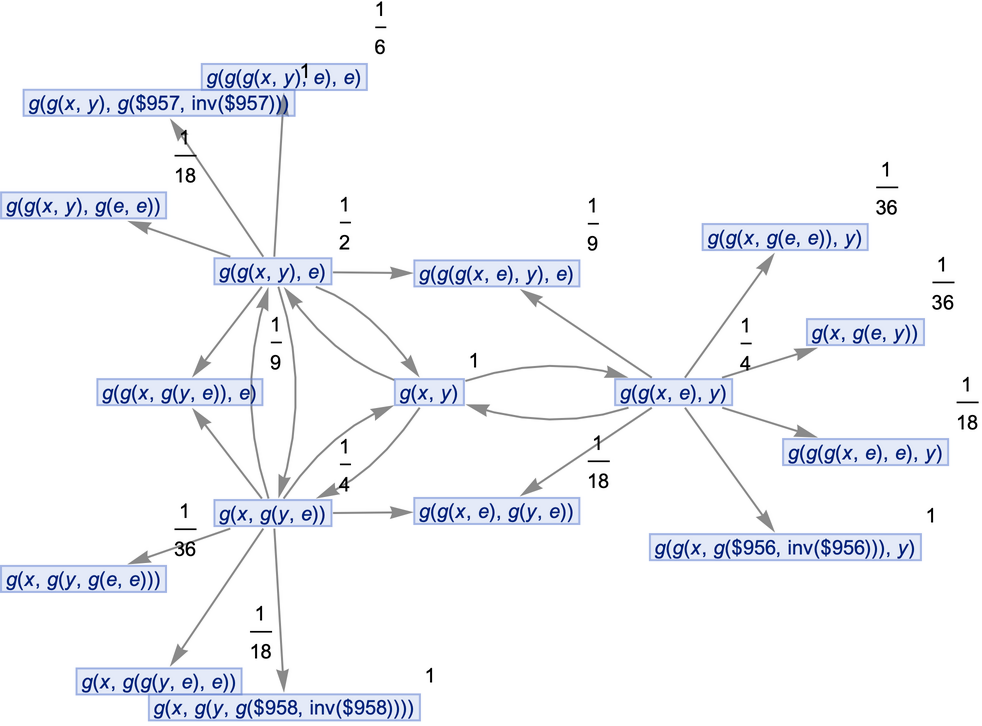
Generate a states graph with vertices weighted by their rate of occurrence on each time step:
| In[27]:= |
![ResourceFunction[
"MultiwayOperatorSystem"][{g[x_, g[y_, z_]] :> g[g[x, y], z], g[g[x_, y_], z_] :> g[x, g[y, z]], g[a_, e] :> a, a_ :> g[a, e], g[a_, inv[a_]] :> e, e :> Module[{a = Unique[]}, g[a, inv[a]]]}, g[x, y], 2, "StatesGraph", "IncludeStateWeights" -> True, VertexLabels -> "VertexWeight"]](https://www.wolframcloud.com/obj/resourcesystem/images/f40/f404faf7-67a6-4fd2-a0a7-f80eebf7c4df/6ff569e9bb8fcc97.png)
|
| Out[27]= |
|
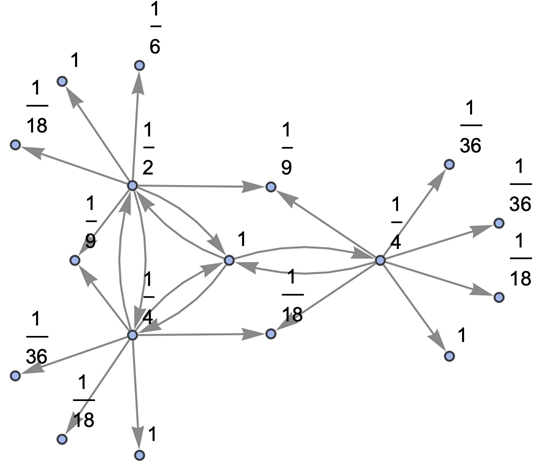
Show the structure of the graph, without labels:
| In[28]:= |
![ResourceFunction[
"MultiwayOperatorSystem"][{g[x_, g[y_, z_]] :> g[g[x, y], z], g[g[x_, y_], z_] :> g[x, g[y, z]], g[a_, e] :> a, a_ :> g[a, e], g[a_, inv[a_]] :> e, e :> Module[{a = Unique[]}, g[a, inv[a]]]}, g[x, y], 2, "StatesGraphStructure", "IncludeStateWeights" -> True, VertexLabels -> "VertexWeight"]](https://www.wolframcloud.com/obj/resourcesystem/images/f40/f404faf7-67a6-4fd2-a0a7-f80eebf7c4df/3dc21abb9db20b96.png)
|
| Out[28]= |
|
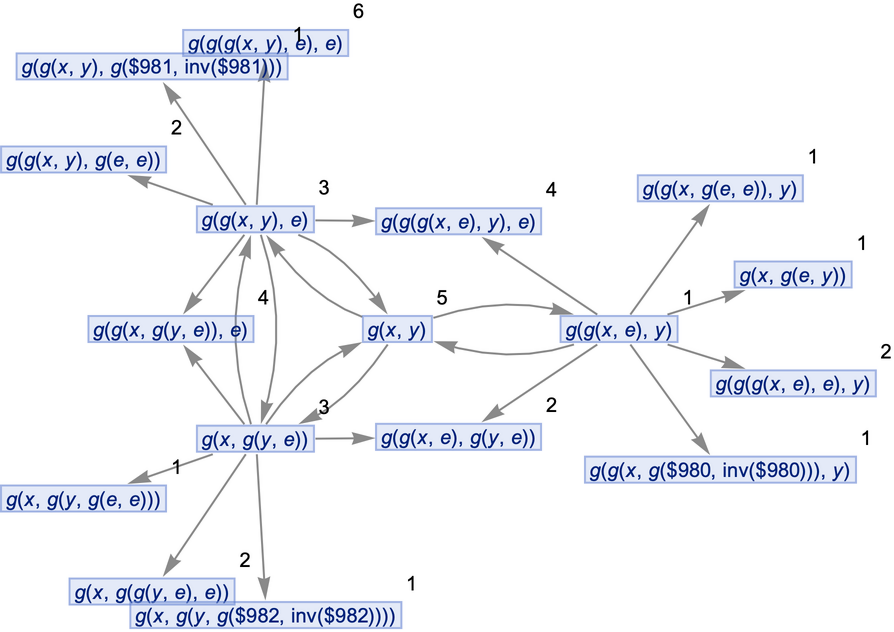
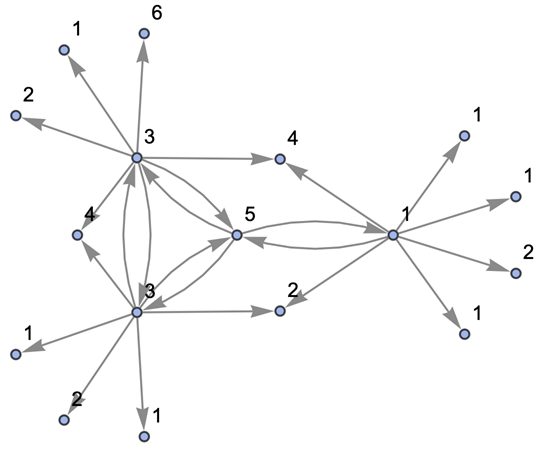
Generate a states graph with vertices weighted by the number of distinct evolution paths that lead to them:
| In[29]:= |
![ResourceFunction[
"MultiwayOperatorSystem"][{g[x_, g[y_, z_]] :> g[g[x, y], z], g[g[x_, y_], z_] :> g[x, g[y, z]], g[a_, e] :> a, a_ :> g[a, e], g[a_, inv[a_]] :> e, e :> Module[{a = Unique[]}, g[a, inv[a]]]}, g[x, y], 2, "StatesGraph", "IncludeStatePathWeights" -> True, VertexLabels -> "VertexWeight"]](https://www.wolframcloud.com/obj/resourcesystem/images/f40/f404faf7-67a6-4fd2-a0a7-f80eebf7c4df/400714d4d14fb7d9.png)
|
| Out[29]= |
|
Show the structure of the graph, without labels:
| In[30]:= |
![ResourceFunction[
"MultiwayOperatorSystem"][{g[x_, g[y_, z_]] :> g[g[x, y], z], g[g[x_, y_], z_] :> g[x, g[y, z]], g[a_, e] :> a, a_ :> g[a, e], g[a_, inv[a_]] :> e, e :> Module[{a = Unique[]}, g[a, inv[a]]]}, g[x, y], 2, "StatesGraphStructure", "IncludeStatePathWeights" -> True, VertexLabels -> "VertexWeight"]](https://www.wolframcloud.com/obj/resourcesystem/images/f40/f404faf7-67a6-4fd2-a0a7-f80eebf7c4df/577d351bb46c4123.png)
|
| Out[30]= |
|
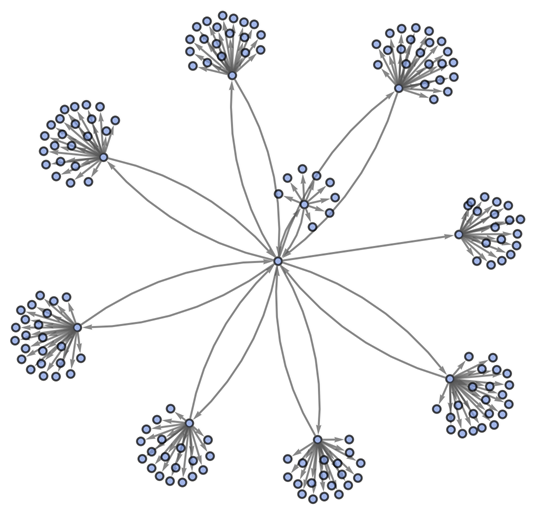
MultiwayOperatorSystem supports all forms of operator axiom systems, including standard Boolean algebra:
| In[31]:= |
![ResourceFunction[
"MultiwayOperatorSystem"][{And[a_, b_] :> And[b, a], Or[a_, b_] :> Or[b, a], And[a_, Or[b_, Not[b_]]] :> a, Or[a_, And[b_, Not[b_]]] :> a, a_ :> Module[{b = Unique[]}, And[a, Or[b, Not[b]]]], a_ :> Module[{b = Unique[]}, Or[a, And[b, Not[b]]]], And[a_, Or[b_, c_]] :> Or[And[a, b], And[a, c]], Or[And[a_, b_], And[a_, c_]] :> And[a, Or[b, c]], Or[a_, And[b_, c_]] :> And[Or[a, b], Or[a, c]], And[Or[a_, b_], Or[a_, c_]] :> Or[a, And[b, c]]}, And[x, y], 2, "StatesGraphStructure"]](https://www.wolframcloud.com/obj/resourcesystem/images/f40/f404faf7-67a6-4fd2-a0a7-f80eebf7c4df/6c1567606d16b578.png)
|
| Out[31]= |
|
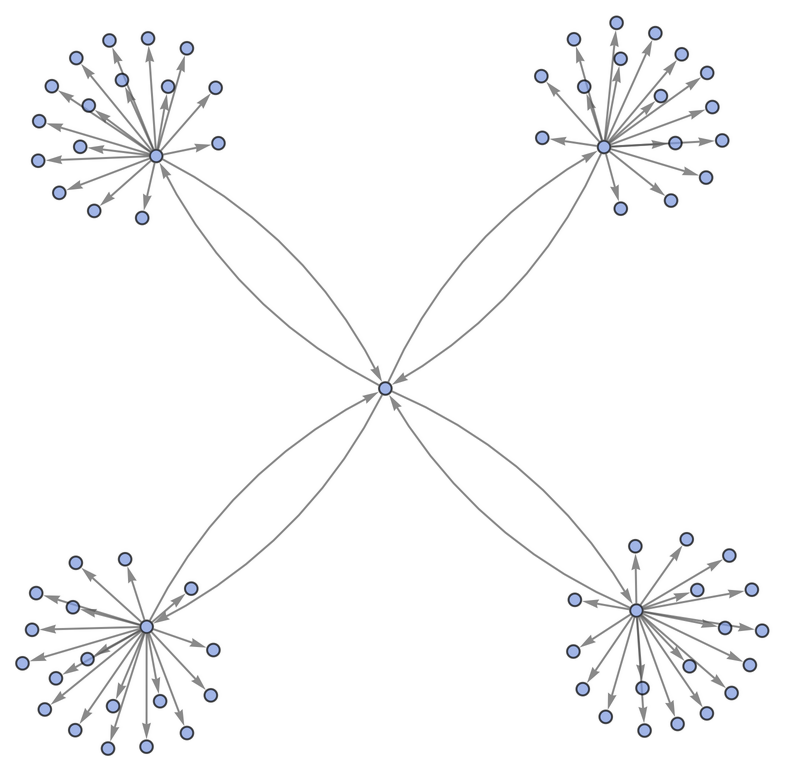
Wolfram's minimal axiom system for Boolean algebra:
| In[32]:= |
![ResourceFunction[
"MultiwayOperatorSystem"][{Nand[Nand[Nand[b_, c_], a_], Nand[b_, Nand[Nand[b_, a_], b_]]] :> a, a_ :> Module[{b = Unique[], c = Unique[]}, Nand[Nand[Nand[b, c], a], Nand[b, Nand[Nand[b, a], b]]]]}, Nand[a, b], 2, "StatesGraphStructure"]](https://www.wolframcloud.com/obj/resourcesystem/images/f40/f404faf7-67a6-4fd2-a0a7-f80eebf7c4df/307ccea3b8f03564.png)
|
| Out[32]= |
|
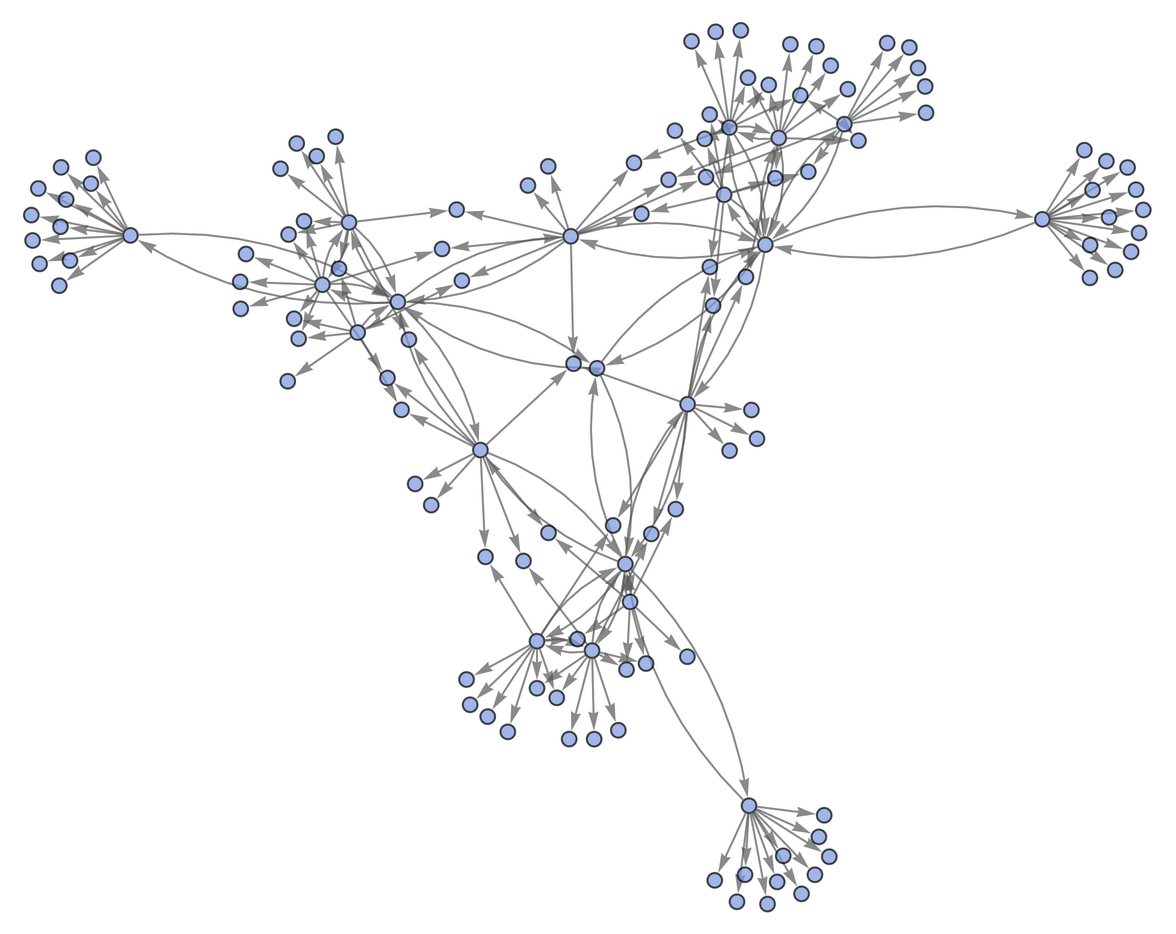
Ring theory:
| In[33]:= |
![ResourceFunction[
"MultiwayOperatorSystem"][{g[a_, g[b_, c_]] :> g[g[a, b], c], g[g[a_, b_], c_] :> g[a, g[b, c]], g[a_, e] :> a, a_ :> g[a, e], g[a_, inv[a_]] :> e, e :> Module[{a = Unique[]}, g[a, inv[a]]], g[a_, b_] :> g[b, a], f[a_, f[b_, c_]] :> f[f[a, b], c], f[f[a_, b_], c_] :> f[a, f[b, c]], f[a_, g[b_, c_]] :> g[f[a, b], f[a, c]], g[f[a_, b_], f[a_, c_]] :> f[a, g[b, c]]}, f[a, b], 3, "StatesGraphStructure"]](https://www.wolframcloud.com/obj/resourcesystem/images/f40/f404faf7-67a6-4fd2-a0a7-f80eebf7c4df/59ce4ab589913f1a.png)
|
| Out[33]= |
|
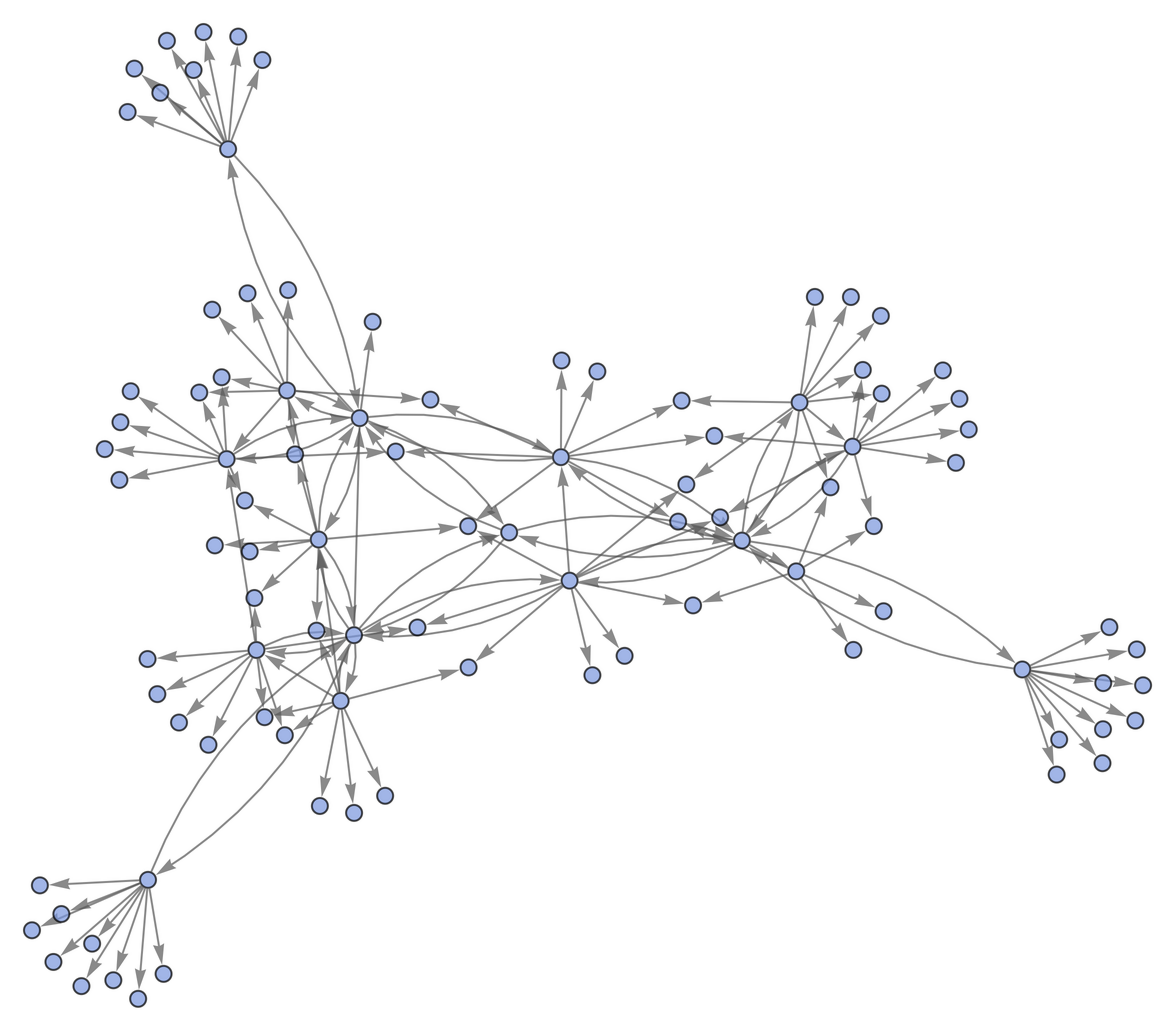
Modified Presburger arithmetic:
| In[34]:= |
![ResourceFunction[
"MultiwayOperatorSystem"][{plus[x_, 0] :> x, x_ :> plus[x, 0], plus[x_, neg[x_]] :> 0, 0 :> Module[{x = Unique[]}, plus[x, neg[x]]], plus[plus[x_, y_], z_] :> plus[x, plus[y, z]], plus[x_, plus[y_, z]] :> plus[plus[x, y], z]}, plus[a, b], 3, "StatesGraphStructure"]](https://www.wolframcloud.com/obj/resourcesystem/images/f40/f404faf7-67a6-4fd2-a0a7-f80eebf7c4df/6362b9beb064801d.png)
|
| Out[34]= |
|
Tarski's axioms of Euclidean geometry:
| In[35]:= |
![(* Evaluate this cell to get the example input *) CloudGet["https://www.wolframcloud.com/obj/60b4d672-e0b0-4b31-a127-877168dc58bc"]](https://www.wolframcloud.com/obj/resourcesystem/images/f40/f404faf7-67a6-4fd2-a0a7-f80eebf7c4df/6fdb5b9c0b83f078.png)
|
| Out[35]= |

|
Note that, in the above, one of the axioms (the axiom of continuity) is actually an axiom schema, which here we represent using a second-order axiom involving operator patterns phi_ and psi_:
| In[36]:= |
|
| Out[36]= |
|
Axiom schemas or higher-order axioms can be represented using operator patterns, such as phi_ in the following specification of the axiom (schema) of induction in Peano arithmetic:
| In[37]:= |
|
| Out[37]= |
|
For instance, use this axiom to prove by induction that prop[m] is true for all m:
| In[38]:= |
|
| Out[38]= |
|
| In[39]:= |
|
| Out[39]= |
|
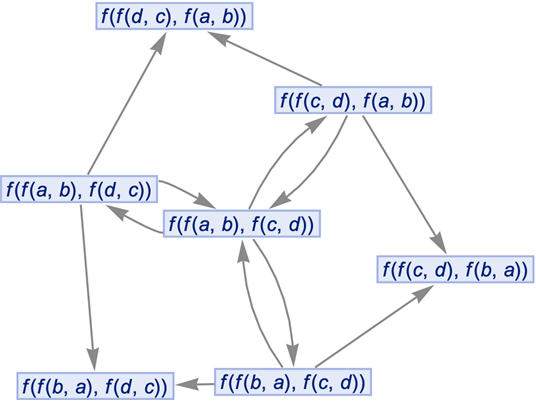
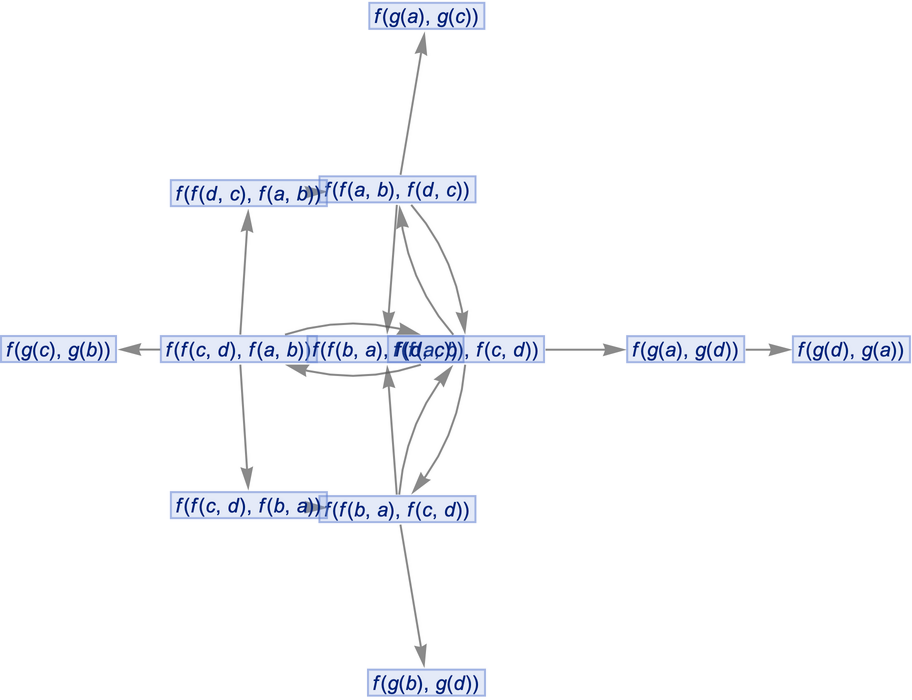
MultiwayOperatorSystem accepts both individual operator axioms and lists of operator axioms:
| In[40]:= |
|
| Out[40]= |
|
| In[41]:= |
|
| Out[41]= |
|
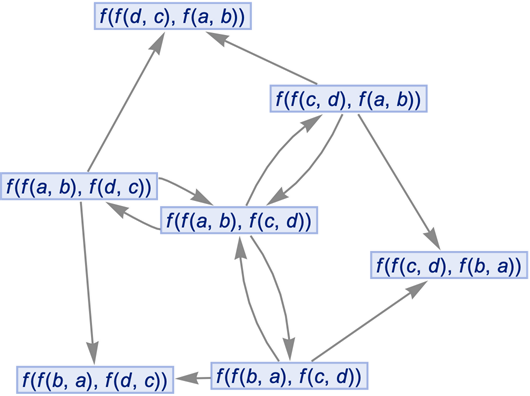
MultiwayOperatorSystem accepts both individual initial conditions and lists of initial conditions:
| In[42]:= |
|
| Out[42]= |
|
| In[43]:= |
|
| Out[43]= |
|
Apply only the first possible event at each step:
| In[44]:= |
![ResourceFunction[
"MultiwayOperatorSystem"][{g[x_, g[y_, z_]] :> g[g[x, y], z], g[g[x_, y_], z_] :> g[x, g[y, z]], g[a_, e] :> a, a_ :> g[a, e], g[a_, inv[a_]] :> e, e :> Module[{a = Unique[]}, g[a, inv[a]]]} -> "Sequential", g[x, y], 3, "StatesGraph"]](https://www.wolframcloud.com/obj/resourcesystem/images/f40/f404faf7-67a6-4fd2-a0a7-f80eebf7c4df/3349fa1e93ec31ef.png)
|
| Out[44]= |
|
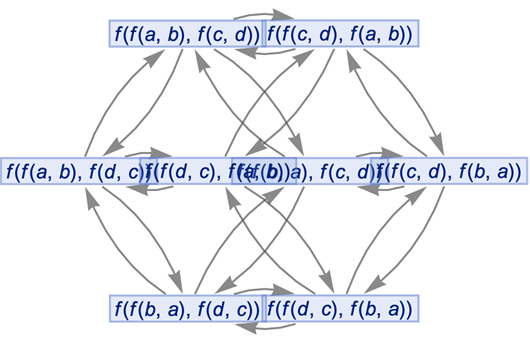
Apply the first and last possible events at each step:
| In[45]:= |
![ResourceFunction[
"MultiwayOperatorSystem"][{g[x_, g[y_, z]] :> g[g[x, y], z], g[g[x_, y_], z_] :> g[x, g[y, z]], g[a_, e] :> a, a_ :> g[a, e], g[a_, inv[a_]] :> e, e :> Module[{a = Unique[]}, g[a, inv[a]]]} -> ({First[#], Last[#]} &), g[x, y], 6, "StatesGraphStructure"]](https://www.wolframcloud.com/obj/resourcesystem/images/f40/f404faf7-67a6-4fd2-a0a7-f80eebf7c4df/642f0c1600f0e9d7.png)
|
| Out[45]= |
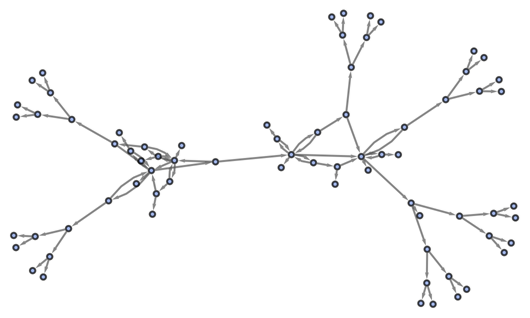
|
By default, states are labeled by their contents:
| In[46]:= |
![ResourceFunction[
"MultiwayOperatorSystem"][{g[x_, g[y_, z_]] :> g[g[x, y], z], g[g[x_, y_], z_] :> g[x, g[y, z]], g[a_, e] :> a, a_ :> g[a, e], g[a_, inv[a_]] :> e, e :> Module[{a = Unique[]}, g[a, inv[a]]]}, g[x, y], 2, "StatesGraph"]](https://www.wolframcloud.com/obj/resourcesystem/images/f40/f404faf7-67a6-4fd2-a0a7-f80eebf7c4df/25ce4a71ed3a9546.png)
|
| Out[46]= |
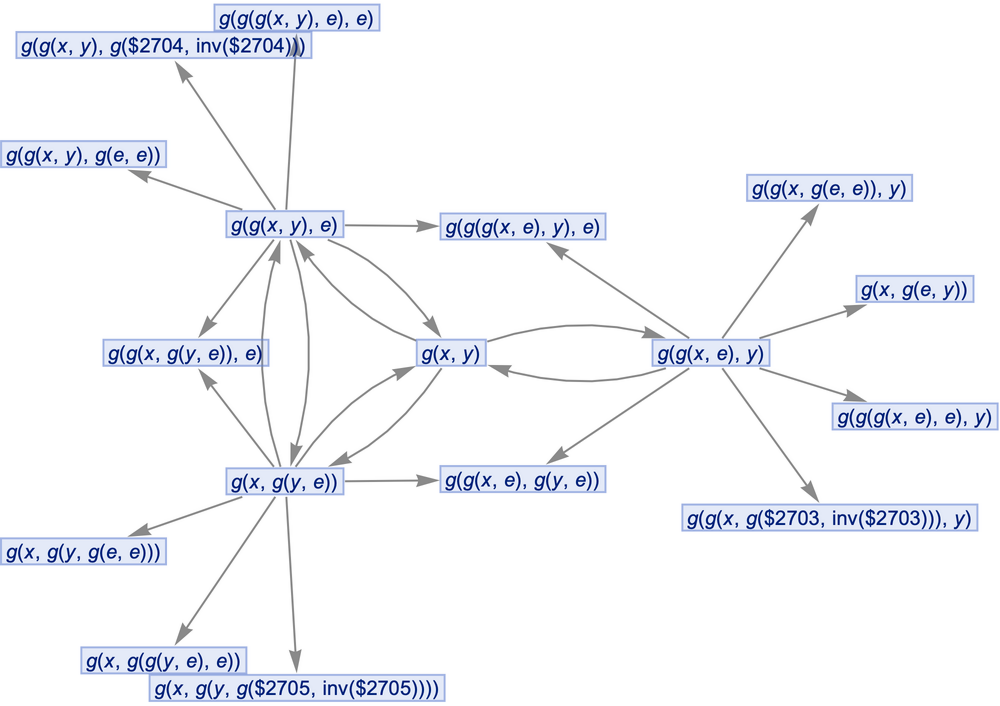
|
Use no labeling for states:
| In[47]:= |
![ResourceFunction[
"MultiwayOperatorSystem"][{g[x_, g[y_, z_]] :> g[g[x, y], z], g[g[x_, y_], z_] :> g[x, g[y, z]], g[a_, e] :> a, a_ :> g[a, e], g[a_, inv[a_]] :> e, e :> Module[{a = Unique[]}, g[a, inv[a]]]}, g[x, y], 2, "StatesGraph", "StateRenderingFunction" -> None]](https://www.wolframcloud.com/obj/resourcesystem/images/f40/f404faf7-67a6-4fd2-a0a7-f80eebf7c4df/569f3f9bfbcb2ced.png)
|
| Out[47]= |
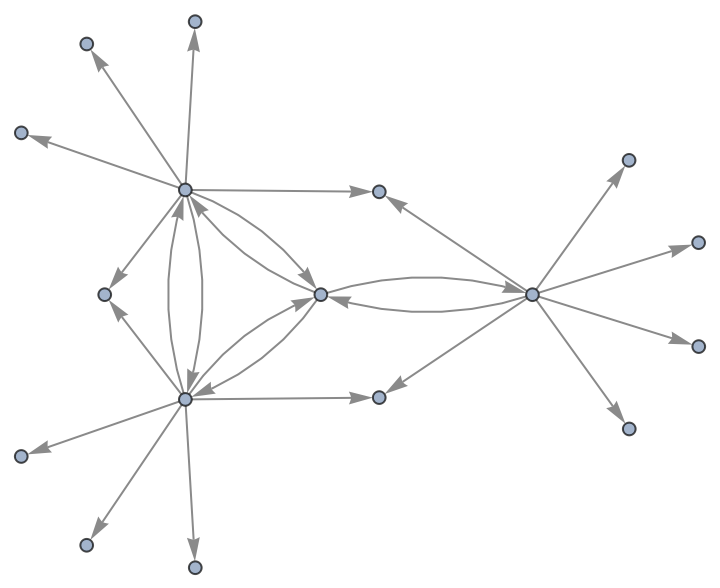
|
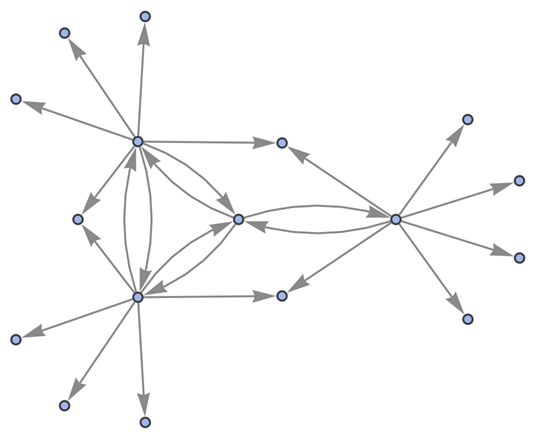
"StatesGraphStructure" yields the same result:
| In[48]:= |
![ResourceFunction[
"MultiwayOperatorSystem"][{g[x_, g[y_, z_]] :> g[g[x, y], z], g[g[x_, y_], z_] :> g[x, g[y, z]], g[a_, e] :> a, a_ :> g[a, e], g[a_, inv[a_]] :> e, e :> Module[{a = Unique[]}, g[a, inv[a]]]}, g[x, y], 2, "StatesGraphStructure"]](https://www.wolframcloud.com/obj/resourcesystem/images/f40/f404faf7-67a6-4fd2-a0a7-f80eebf7c4df/5d374c0e727e4ee8.png)
|
| Out[48]= |
|
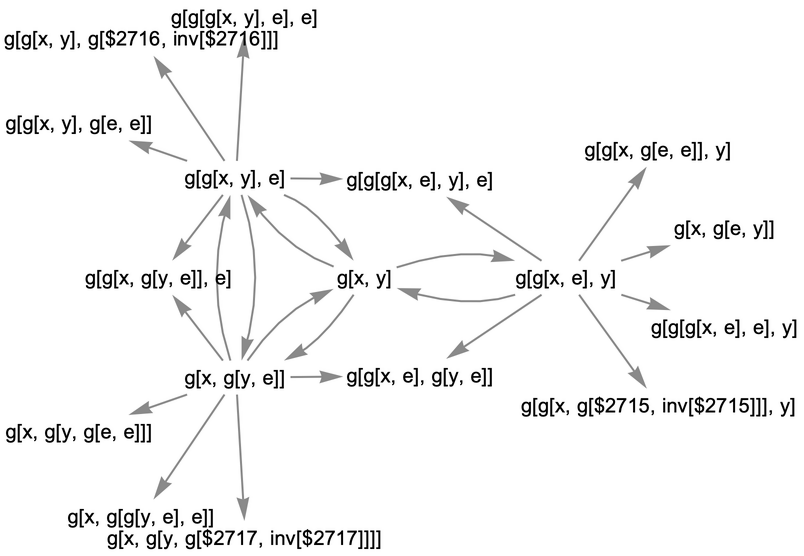
Use raw state names as node labels:
| In[49]:= |
![ResourceFunction[
"MultiwayOperatorSystem"][{g[x_, g[y_, z_]] :> g[g[x, y], z], g[g[x_, y_], z_] :> g[x, g[y, z]], g[a_, e] :> a, a_ :> g[a, e], g[a_, inv[a_]] :> e, e :> Module[{a = Unique[]}, g[a, inv[a]]]}, g[x, y], 2, "StatesGraph", "StateRenderingFunction" -> Inherited]](https://www.wolframcloud.com/obj/resourcesystem/images/f40/f404faf7-67a6-4fd2-a0a7-f80eebf7c4df/7c72341f17809e98.png)
|
| Out[49]= |
|
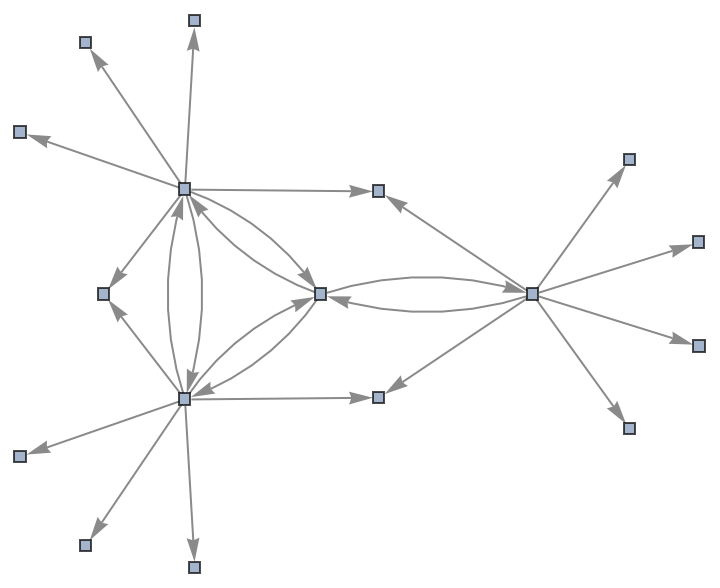
Use a named shape as each state label:
| In[50]:= |
![ResourceFunction[
"MultiwayOperatorSystem"][{g[x_, g[y_, z_]] :> g[g[x, y], z], g[g[x_, y_], z_] :> g[x, g[y, z]], g[a_, e] :> a, a_ :> g[a, e], g[a_, inv[a_]] :> e, e :> Module[{a = Unique[]}, g[a, inv[a]]]}, g[x, y], 2, "StatesGraph", "StateRenderingFunction" -> "Square"]](https://www.wolframcloud.com/obj/resourcesystem/images/f40/f404faf7-67a6-4fd2-a0a7-f80eebf7c4df/0d13fe8799c637b7.png)
|
| Out[50]= |
|
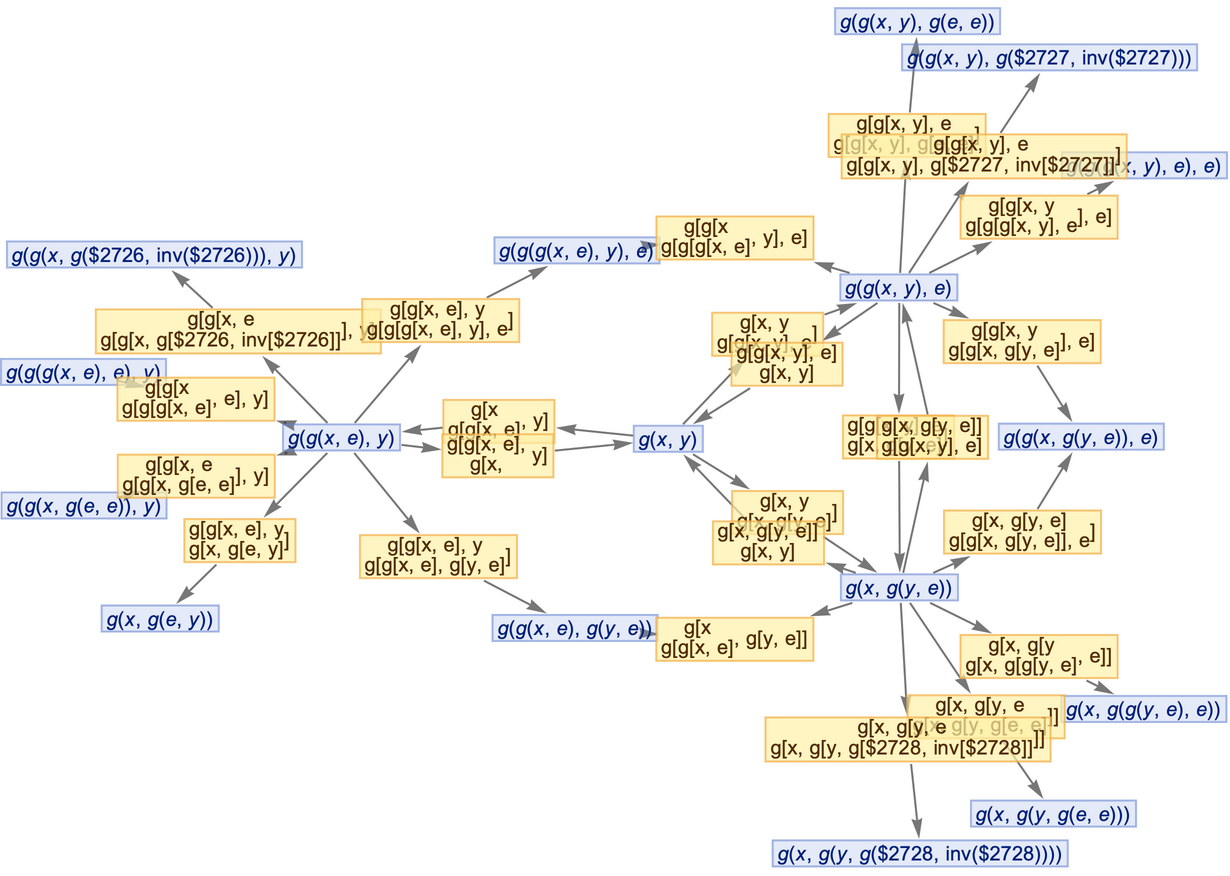
By default, both states and events are labeled by their contents:
| In[51]:= |
![ResourceFunction[
"MultiwayOperatorSystem"][{g[x_, g[y_, z_]] :> g[g[x, y], z], g[g[x_, y_], z_] :> g[x, g[y, z]], g[a_, e] :> a, a_ :> g[a, e], g[a_, inv[a_]] :> e, e :> Module[{a = Unique[]}, g[a, inv[a]]]}, g[x, y], 2, "EvolutionEventsGraph"]](https://www.wolframcloud.com/obj/resourcesystem/images/f40/f404faf7-67a6-4fd2-a0a7-f80eebf7c4df/17ed88d086a08dcf.png)
|
| Out[51]= |
|
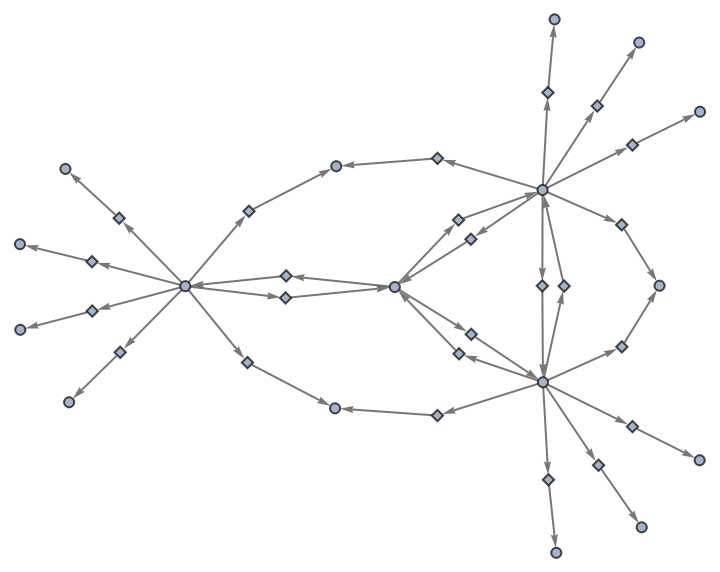
Use no labels for states or events:
| In[52]:= |
![ResourceFunction[
"MultiwayOperatorSystem"][{g[x_, g[y_, z_]] :> g[g[x, y], z], g[g[x_, y_], z_] :> g[x, g[y, z]], g[a_, e] :> a, a_ :> g[a, e], g[a_, inv[a_]] :> e, e :> Module[{a = Unique[]}, g[a, inv[a]]]}, g[x, y], 2, "EvolutionEventsGraph", "StateRenderingFunction" -> None,
"EventRenderingFunction" -> None]](https://www.wolframcloud.com/obj/resourcesystem/images/f40/f404faf7-67a6-4fd2-a0a7-f80eebf7c4df/1e403c547afb0a3d.png)
|
| Out[52]= |
|
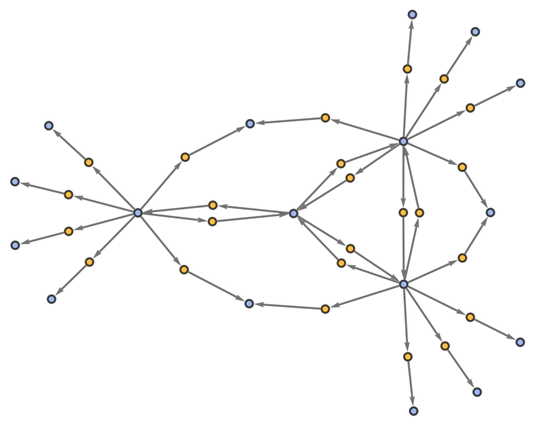
"EvolutionEventsGraphStructure" yields an equivalent result:
| In[53]:= |
![ResourceFunction[
"MultiwayOperatorSystem"][{g[x_, g[y_, z_]] :> g[g[x, y], z], g[g[x_, y_], z_] :> g[x, g[y, z]], g[a_, e] :> a, a_ :> g[a, e], g[a_, inv[a_]] :> e, e :> Module[{a = Unique[]}, g[a, inv[a]]]}, g[x, y], 2, "EvolutionEventsGraphStructure"]](https://www.wolframcloud.com/obj/resourcesystem/images/f40/f404faf7-67a6-4fd2-a0a7-f80eebf7c4df/33f8e747c4c7e4ae.png)
|
| Out[53]= |
|
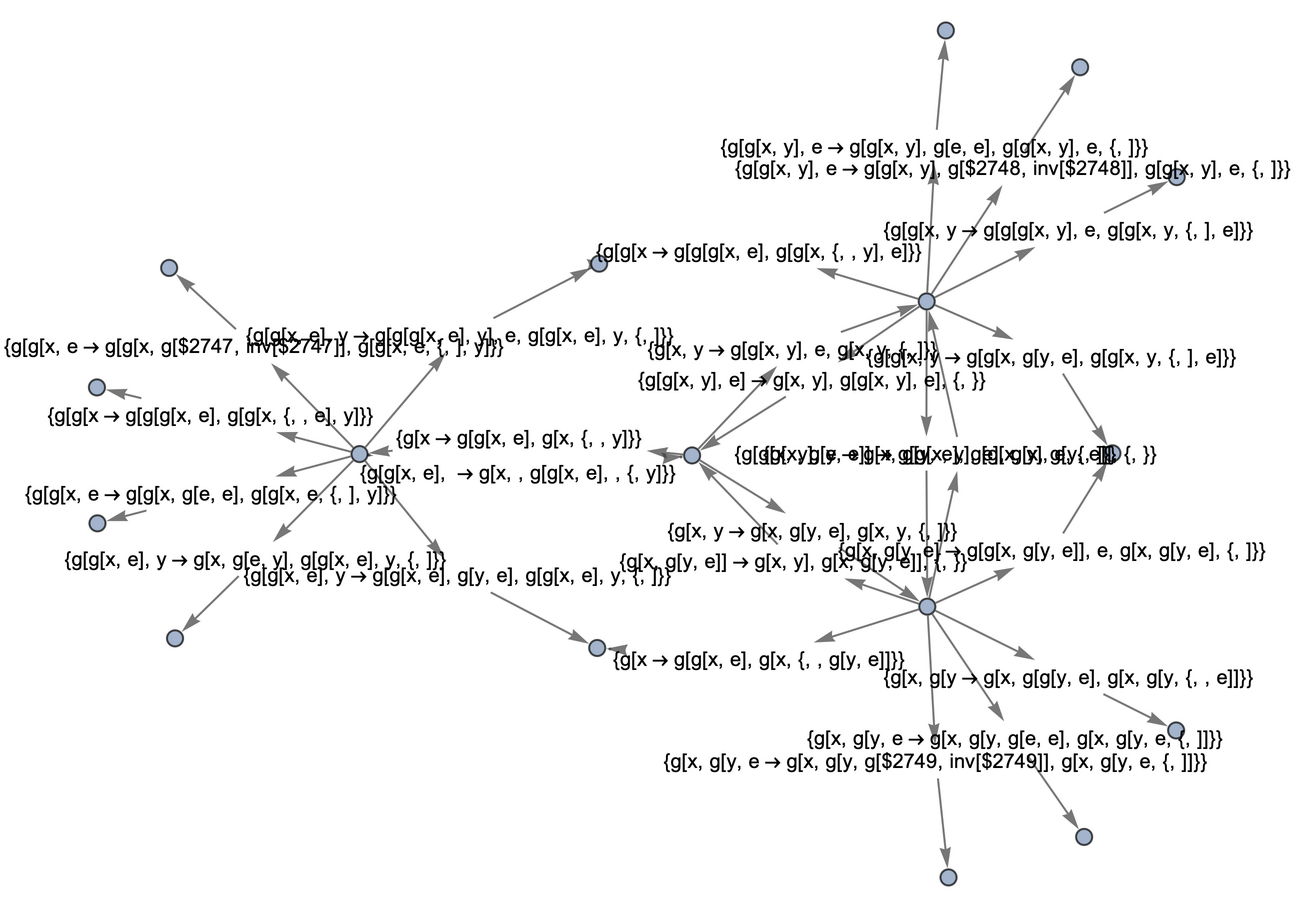
Use raw event expressions as their labels:
| In[54]:= |
![ResourceFunction[
"MultiwayOperatorSystem"][{g[x_, g[y_, z_]] :> g[g[x, y], z], g[g[x_, y_], z_] :> g[x, g[y, z]], g[a_, e] :> a, a_ :> g[a, e], g[a_, inv[a_]] :> e, e :> Module[{a = Unique[]}, g[a, inv[a]]]}, g[x, y], 2, "EvolutionEventsGraph", "StateRenderingFunction" -> None,
"EventRenderingFunction" -> Inherited]](https://www.wolframcloud.com/obj/resourcesystem/images/f40/f404faf7-67a6-4fd2-a0a7-f80eebf7c4df/05b20ab2b019cf64.png)
|
| Out[54]= |
|
By default, "AllEventsList" does not include initialization events:
| In[55]:= |
![ResourceFunction[
"MultiwayOperatorSystem"][{g[x_, g[y_, z_]] :> g[g[x, y], z], g[g[x_, y_], z_] :> g[x, g[y, z]], g[a_, e] :> a, a_ :> g[a, e], g[a_, inv[a_]] :> e, e :> Module[{a = Unique[]}, g[a, inv[a]]]}, g[x, y], 2, "AllEventsList"]](https://www.wolframcloud.com/obj/resourcesystem/images/f40/f404faf7-67a6-4fd2-a0a7-f80eebf7c4df/38b8786febcdb9bf.png)
|
| Out[55]= |
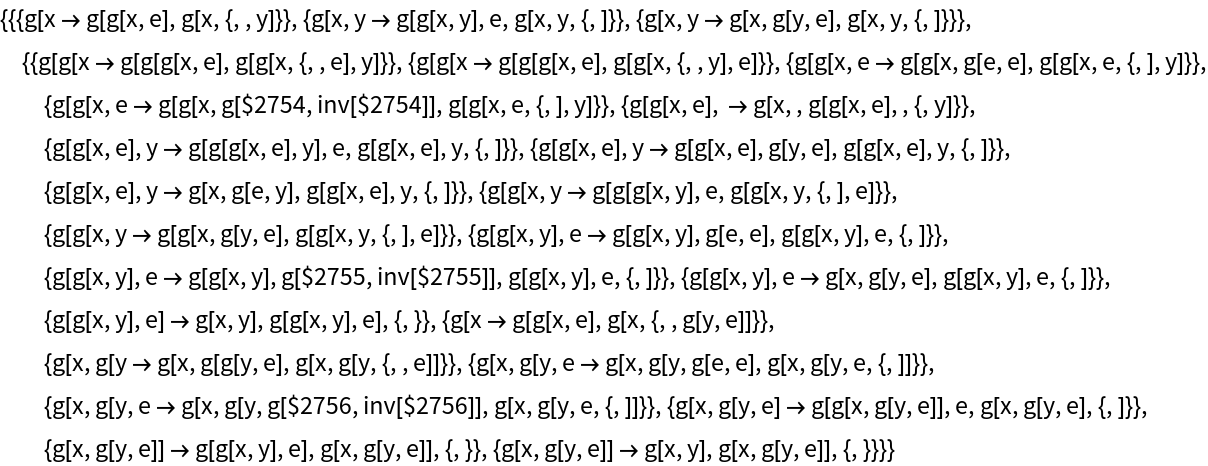
|
The option "IncludeInitializationEvents" allows one to override this default:
| In[56]:= |
![ResourceFunction[
"MultiwayOperatorSystem"][{g[x_, g[y_, z_]] :> g[g[x, y], z], g[g[x_, y_], z_] :> g[x, g[y, z]], g[a_, e] :> a, a_ :> g[a, e], g[a_, inv[a_]] :> e, e :> Module[{a = Unique[]}, g[a, inv[a]]]}, g[x, y], 2, "AllEventsList", "IncludeInitializationEvents" -> True]](https://www.wolframcloud.com/obj/resourcesystem/images/f40/f404faf7-67a6-4fd2-a0a7-f80eebf7c4df/7988b72ece2d0d70.png)
|
| Out[56]= |
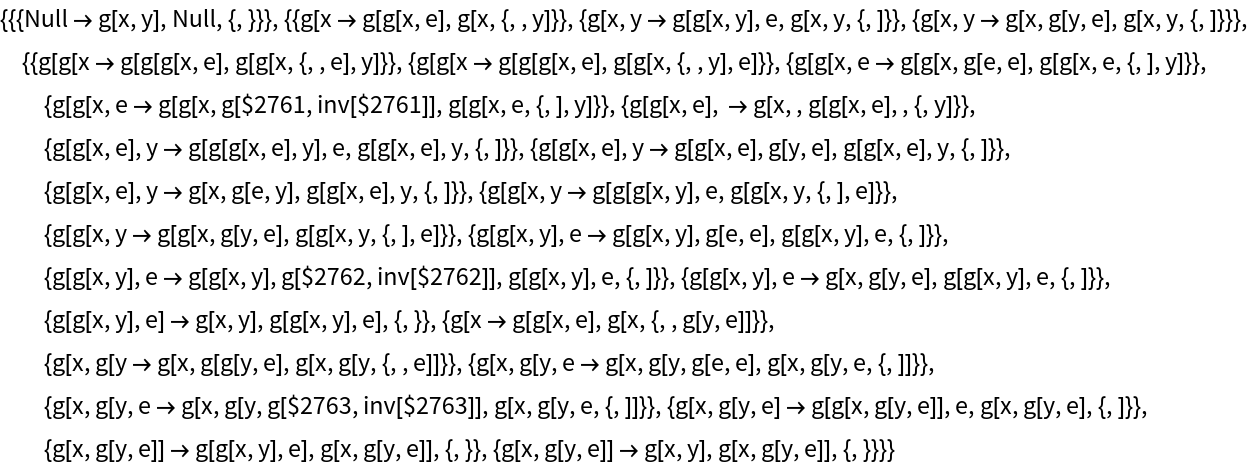
|
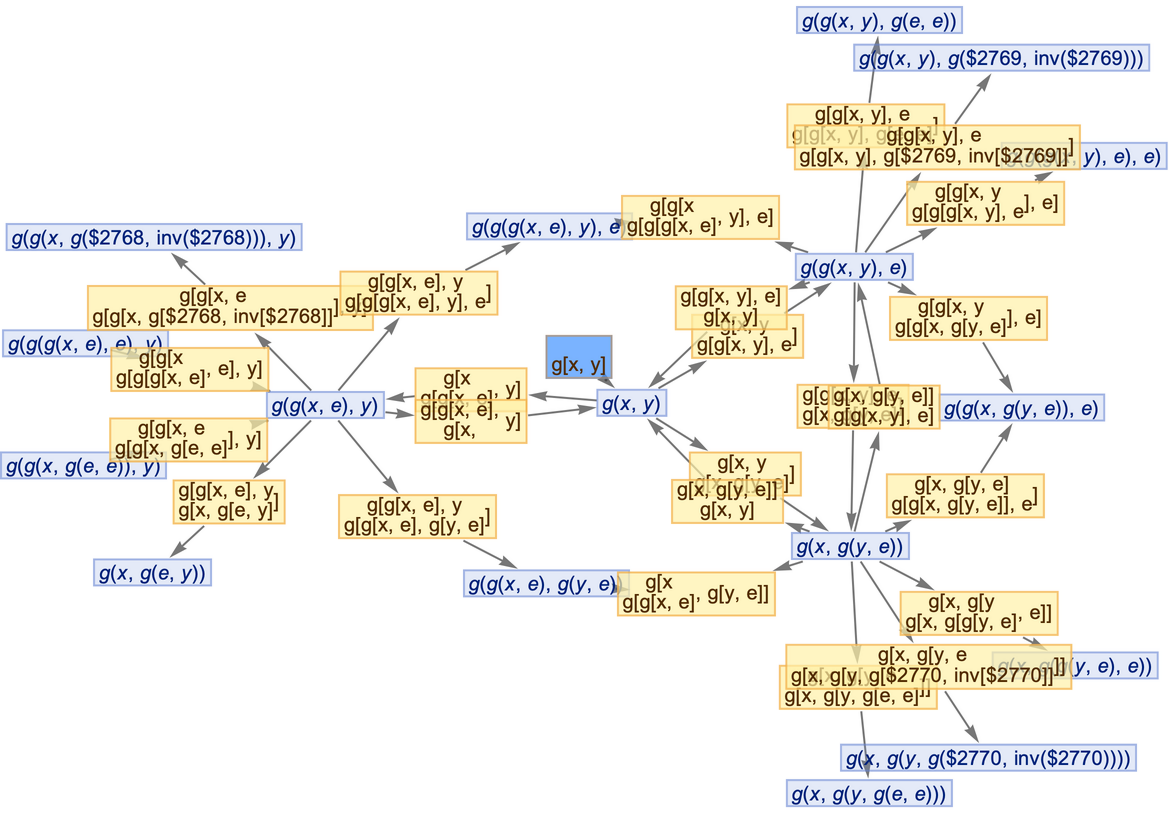
Initialization events have special default rendering:
| In[57]:= |
![ResourceFunction[
"MultiwayOperatorSystem"][{g[x_, g[y_, z_]] :> g[g[x, y], z], g[g[x_, y_], z_] :> g[x, g[y, z]], g[a_, e] :> a, a_ :> g[a, e], g[a_, inv[a_]] :> e, e :> Module[{a = Unique[]}, g[a, inv[a]]]}, g[x, y], 2, "EvolutionEventsGraph", "IncludeInitializationEvents" -> True]](https://www.wolframcloud.com/obj/resourcesystem/images/f40/f404faf7-67a6-4fd2-a0a7-f80eebf7c4df/53f6c252a369781d.png)
|
| Out[57]= |
|
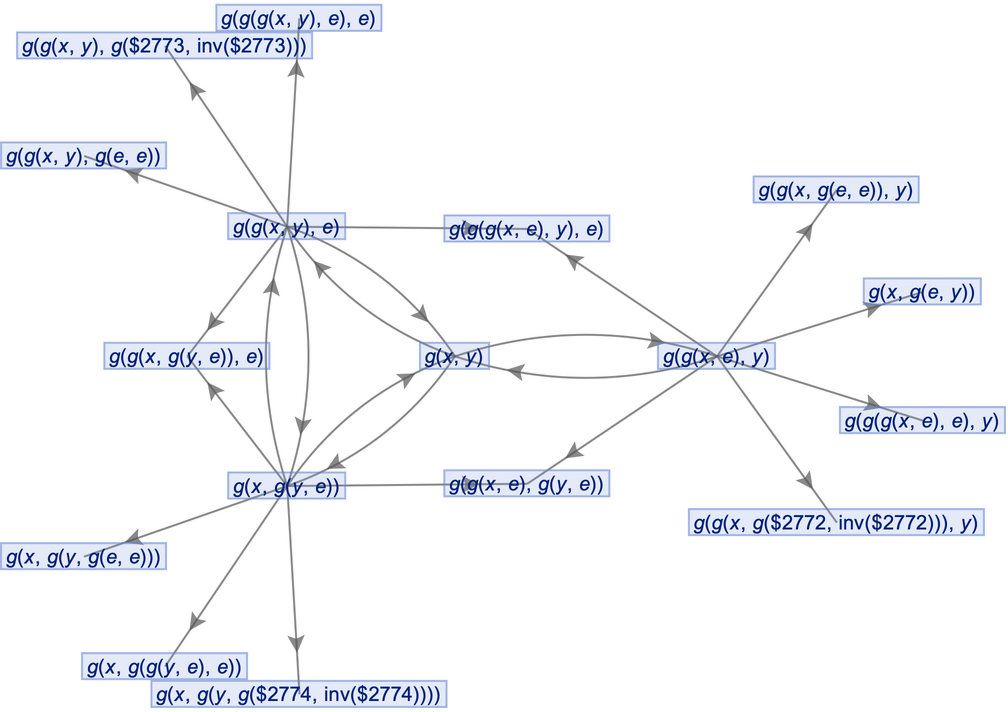
Place arrows in the middle of edges:
| In[58]:= |
![ResourceFunction[
"MultiwayOperatorSystem"][{g[x_, g[y_, z_]] :> g[g[x, y], z], g[g[x_, y_], z_] :> g[x, g[y, z]], g[a_, e] :> a, a_ :> g[a, e], g[a_, inv[a_]] :> e, e :> Module[{a = Unique[]}, g[a, inv[a]]]}, g[x, y], 2, "StatesGraph", EdgeShapeFunction -> GraphElementData["ShortFilledArrow", "ArrowSize" -> 0.03], VertexSize -> 1]](https://www.wolframcloud.com/obj/resourcesystem/images/f40/f404faf7-67a6-4fd2-a0a7-f80eebf7c4df/56f3e0c5ca266c9f.png)
|
| Out[58]= |
|
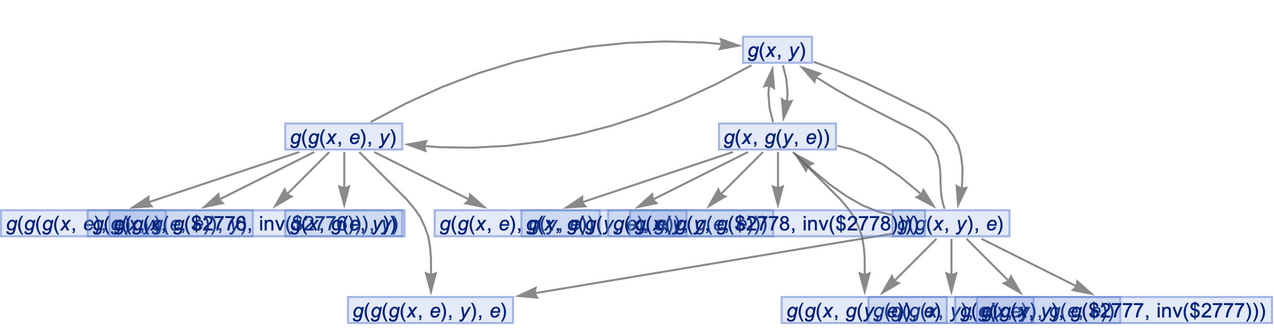
Force the initial state node to be at the top:
| In[59]:= |
![ResourceFunction[
"MultiwayOperatorSystem"][{g[x_, g[y_, z_]] :> g[g[x, y], z], g[g[x_, y_], z_] :> g[x, g[y, z]], g[a_, e] :> a, a_ :> g[a, e], g[a_, inv[a_]] :> e, e :> Module[{a = Unique[]}, g[a, inv[a]]]}, g[x, y], 2, "StatesGraph", GraphLayout -> {"LayeredDigraphEmbedding", "RootVertex" -> ToString[g[x, y]]}]](https://www.wolframcloud.com/obj/resourcesystem/images/f40/f404faf7-67a6-4fd2-a0a7-f80eebf7c4df/343fd62523d84656.png)
|
| Out[59]= |
|
By default, equivalent states are merged across all time steps:
| In[60]:= |
![ResourceFunction[
"MultiwayOperatorSystem"][{g[x_, g[y_, z_]] :> g[g[x, y], z], g[g[x_, y_], z_] :> g[x, g[y, z]], g[a_, e] :> a, a_ :> g[a, e], g[a_, inv[a_]] :> e, e :> Module[{a = Unique[]}, g[a, inv[a]]]}, g[x, y], 2, "StatesGraph"]](https://www.wolframcloud.com/obj/resourcesystem/images/f40/f404faf7-67a6-4fd2-a0a7-f80eebf7c4df/2bf644783a3a7dee.png)
|
| Out[60]= |

|
| In[61]:= |
![ResourceFunction[
"MultiwayOperatorSystem"][{g[x_, g[y_, z_]] :> g[g[x, y], z], g[g[x_, y_], z_] :> g[x, g[y, z]], g[a_, e] :> a, a_ :> g[a, e], g[a_, inv[a_]] :> e, e :> Module[{a = Unique[]}, g[a, inv[a]]]}, g[x, y], 2, "AllStatesList"]](https://www.wolframcloud.com/obj/resourcesystem/images/f40/f404faf7-67a6-4fd2-a0a7-f80eebf7c4df/3d8ca056930dc1bc.png)
|
| Out[61]= |

|
Merging of equivalent states across different time steps can be prevented by including step numbers:
| In[62]:= |
![ResourceFunction[
"MultiwayOperatorSystem"][{g[x_, g[y_, z_]] :> g[g[x, y], z], g[g[x_, y_], z_] :> g[x, g[y, z]], g[a_, e] :> a, a_ :> g[a, e], g[a_, inv[a_]] :> e, e :> Module[{a = Unique[]}, g[a, inv[a]]]}, g[x, y], 2, "StatesGraph", "IncludeStepNumber" -> True]](https://www.wolframcloud.com/obj/resourcesystem/images/f40/f404faf7-67a6-4fd2-a0a7-f80eebf7c4df/591aa1d85e5d232a.png)
|
| Out[62]= |

|
List the states:
| In[63]:= |
![ResourceFunction[
"MultiwayOperatorSystem"][{g[x_, g[y_, z_]] :> g[g[x, y], z], g[g[x_, y_], z_] :> g[x, g[y, z]], g[a_, e] :> a, a_ :> g[a, e], g[a_, inv[a_]] :> e, e :> Module[{a = Unique[]}, g[a, inv[a]]]}, g[x, y], 2, "AllStatesList", "IncludeStepNumber" -> True]](https://www.wolframcloud.com/obj/resourcesystem/images/f40/f404faf7-67a6-4fd2-a0a7-f80eebf7c4df/39f25c7a210a3923.png)
|
| Out[63]= |
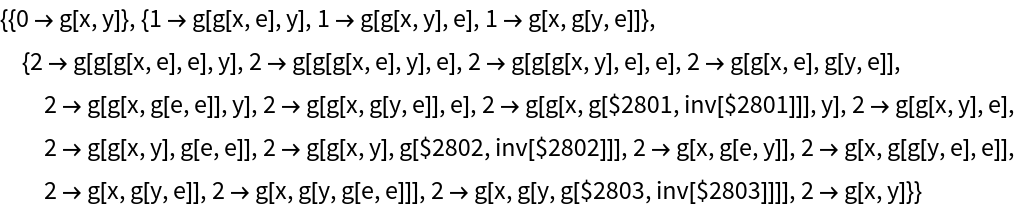
|
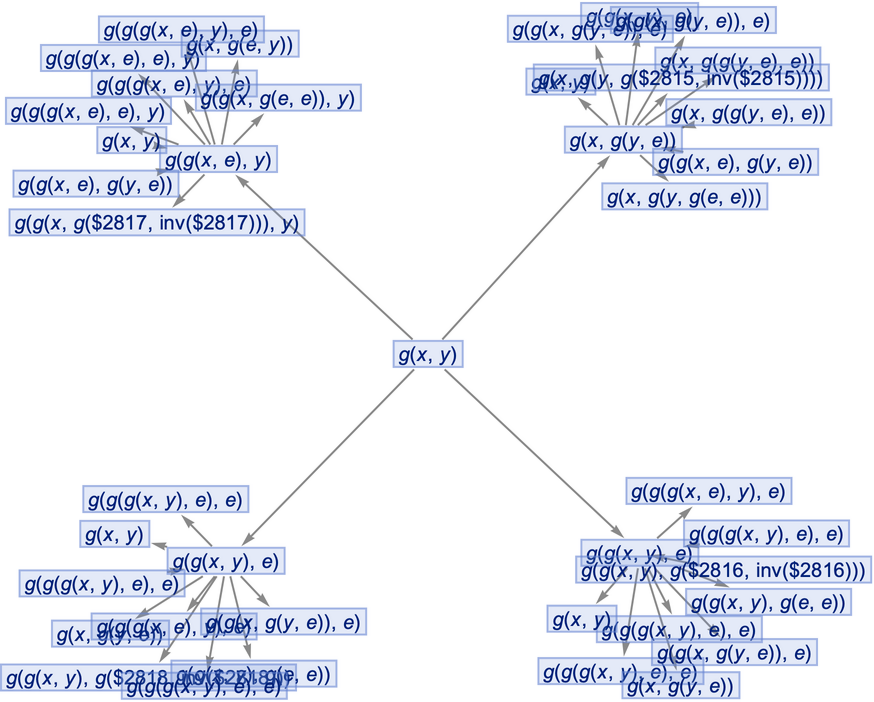
Merging of equivalent states at the same time step can be prevented by also including state IDs:
| In[64]:= |
![ResourceFunction[
"MultiwayOperatorSystem"][{g[x_, g[y_, z_]] :> g[g[x, y], z], g[g[x_, y_], z_] :> g[x, g[y, z]], g[a_, e] :> a, a_ :> g[a, e], g[a_, inv[a_]] :> e, e :> Module[{a = Unique[]}, g[a, inv[a]]]}, g[x, y], 2, "StatesGraph", "IncludeStepNumber" -> True, "IncludeStateID" -> True, GraphLayout -> "SpringElectricalEmbedding"]](https://www.wolframcloud.com/obj/resourcesystem/images/f40/f404faf7-67a6-4fd2-a0a7-f80eebf7c4df/05c83422527ea480.png)
|
| Out[64]= |
|
List the states:
| In[65]:= |
![ResourceFunction[
"MultiwayOperatorSystem"][{g[x_, g[y_, z_]] :> g[g[x, y], z], g[g[x_, y_], z_] :> g[x, g[y, z]], g[a_, e] :> a, a_ :> g[a, e], g[a_, inv[a_]] :> e, e :> Module[{a = Unique[]}, g[a, inv[a]]]}, g[x, y], 2, "AllStatesList", "IncludeStepNumber" -> True, "IncludeStateID" -> True]](https://www.wolframcloud.com/obj/resourcesystem/images/f40/f404faf7-67a6-4fd2-a0a7-f80eebf7c4df/50480f035d14fdec.png)
|
| Out[65]= |

|
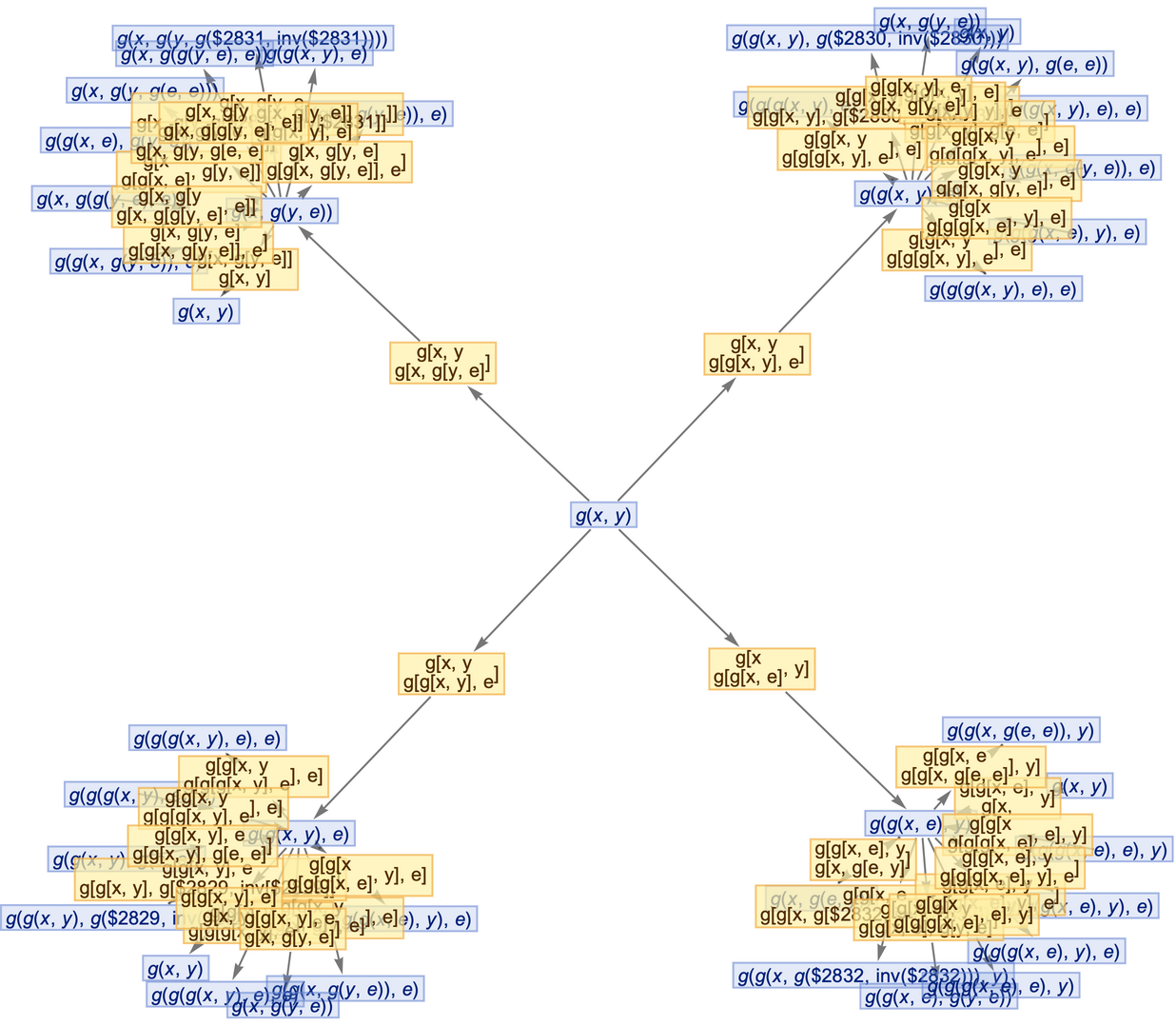
Step numbers and IDs also apply to events:
| In[66]:= |
![ResourceFunction[
"MultiwayOperatorSystem"][{g[x_, g[y_, z_]] :> g[g[x, y], z], g[g[x_, y_], z_] :> g[x, g[y, z]], g[a_, e] :> a, a_ :> g[a, e], g[a_, inv[a_]] :> e, e :> Module[{a = Unique[]}, g[a, inv[a]]]}, g[x, y], 2, "EvolutionEventsGraph", "IncludeStepNumber" -> True, "IncludeStateID" -> True]](https://www.wolframcloud.com/obj/resourcesystem/images/f40/f404faf7-67a6-4fd2-a0a7-f80eebf7c4df/7c0a3433cbf6cfe1.png)
|
| Out[66]= |
|
See the events:
| In[67]:= |
![ResourceFunction[
"MultiwayOperatorSystem"][{g[x_, g[y_, z_]] :> g[g[x, y], z], g[g[x_, y_], z_] :> g[x, g[y, z]], g[a_, e] :> a, a_ :> g[a, e], g[a_, inv[a_]] :> e, e :> Module[{a = Unique[]}, g[a, inv[a]]]}, g[x, y], 2, "AllEventsList", "IncludeStepNumber" -> True, "IncludeStateID" -> True]](https://www.wolframcloud.com/obj/resourcesystem/images/f40/f404faf7-67a6-4fd2-a0a7-f80eebf7c4df/68d60597b3b1df19.png)
|
| Out[67]= |

|
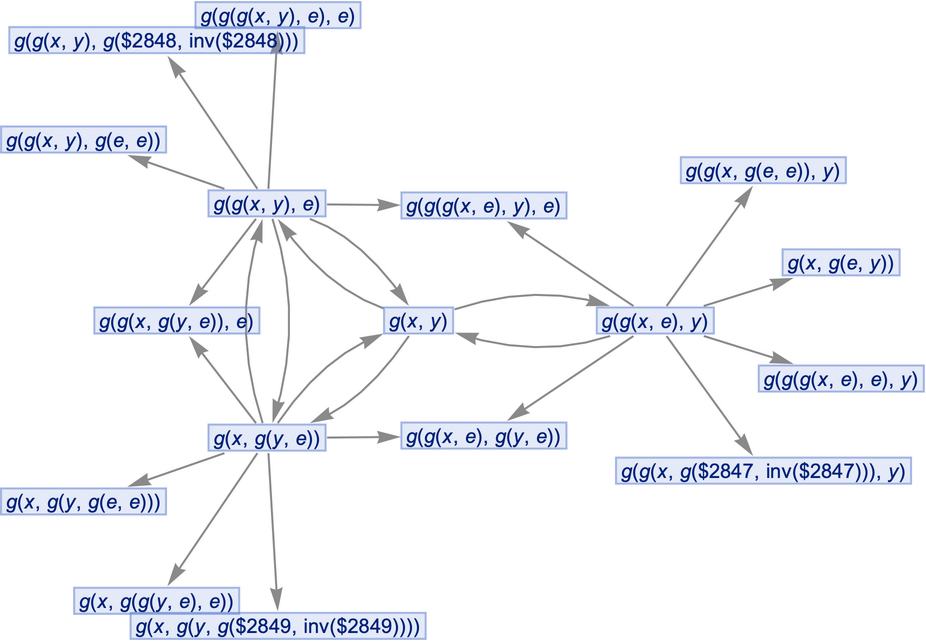
By default, multiple instances of equivalent updating events are merged in the states graph:
| In[68]:= |
![ResourceFunction[
"MultiwayOperatorSystem"][{g[x_, g[y_, z_]] :> g[g[x, y], z], g[g[x_, y_], z_] :> g[x, g[y, z]], g[a_, e] :> a, a_ :> g[a, e], g[a_, inv[a_]] :> e, e :> Module[{a = Unique[]}, g[a, inv[a]]]}, g[x, y], 2, "StatesGraph"]](https://www.wolframcloud.com/obj/resourcesystem/images/f40/f404faf7-67a6-4fd2-a0a7-f80eebf7c4df/6efa3acfce57c438.png)
|
| Out[68]= |
|
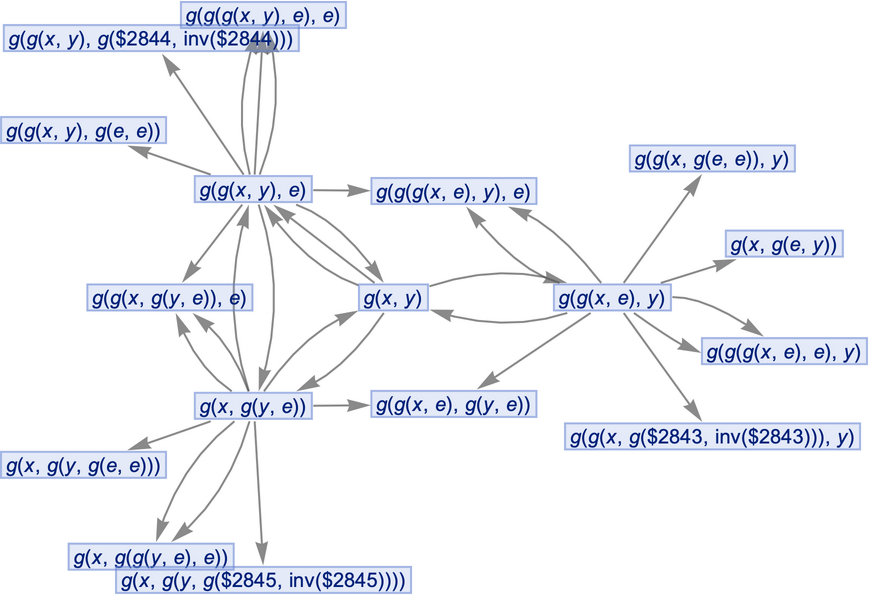
Merging of equivalent events can be prevented by including event instances:
| In[69]:= |
![ResourceFunction[
"MultiwayOperatorSystem"][{g[x_, g[y_, z_]] :> g[g[x, y], z], g[g[x_, y_], z_] :> g[x, g[y, z]], g[a_, e] :> a, a_ :> g[a, e], g[a_, inv[a_]] :> e, e :> Module[{a = Unique[]}, g[a, inv[a]]]}, g[x, y], 2, "StatesGraph", "IncludeEventInstances" -> True]](https://www.wolframcloud.com/obj/resourcesystem/images/f40/f404faf7-67a6-4fd2-a0a7-f80eebf7c4df/6ab463cf698d21bf.png)
|
| Out[69]= |
|
Vertices of a states graph can be weighted by their relative rate of occurrence at each time step:
| In[70]:= |
![ResourceFunction[
"MultiwayOperatorSystem"][{g[x_, g[y_, z_]] :> g[g[x, y], z], g[g[x_, y_], z_] :> g[x, g[y, z]], g[a_, e] :> a, a_ :> g[a, e], g[a_, inv[a_]] :> e, e :> Module[{a = Unique[]}, g[a, inv[a]]]}, g[x, y], 2, "StatesGraph", "IncludeStateWeights" -> True, VertexLabels -> "VertexWeight"]](https://www.wolframcloud.com/obj/resourcesystem/images/f40/f404faf7-67a6-4fd2-a0a7-f80eebf7c4df/261e61980155512a.png)
|
| Out[70]= |

|
Vertices can also be weighted by the number of distinct evolution paths that lead to them:
| In[71]:= |
![ResourceFunction[
"MultiwayOperatorSystem"][{g[x_, g[y_, z_]] :> g[g[x, y], z], g[g[x_, y_], z_] :> g[x, g[y, z]], g[a_, e] :> a, a_ :> g[a, e], g[a_, inv[a_]] :> e, e :> Module[{a = Unique[]}, g[a, inv[a]]]}, g[x, y], 2, "StatesGraph", "IncludeStatePathWeights" -> True, VertexLabels -> "VertexWeight"]](https://www.wolframcloud.com/obj/resourcesystem/images/f40/f404faf7-67a6-4fd2-a0a7-f80eebf7c4df/32b0dee3dd298c96.png)
|
| Out[71]= |

|
By default, "CausalGraphInstances" returns all possible causal graphs:
| In[72]:= |
![ResourceFunction[
"MultiwayOperatorSystem"][{g[x_, g[y_, z_]] :> g[g[x, y], z], g[g[x_, y_], z_] :> g[x, g[y, z]], g[a_, e] :> a, a_ :> g[a, e], g[a_, inv[a_]] :> e, e :> Module[{a = Unique[]}, g[a, inv[a]]]}, g[x, y], 3, "CausalGraphInstances"] // Length](https://www.wolframcloud.com/obj/resourcesystem/images/f40/f404faf7-67a6-4fd2-a0a7-f80eebf7c4df/16bcc71b7eb9a9cb.png)
|
| Out[72]= |
|
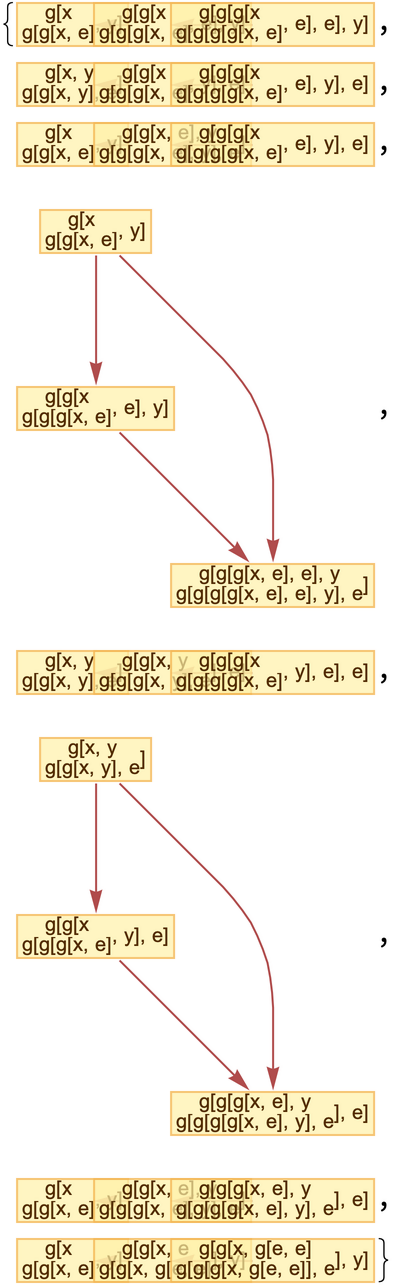
The number of causal graphs returned can be limited using MaxItems:
| In[73]:= |
![ResourceFunction[
"MultiwayOperatorSystem"][{g[x_, g[y_, z_]] :> g[g[x, y], z], g[g[x_, y_], z_] :> g[x, g[y, z]], g[a_, e] :> a, a_ :> g[a, e], g[a_, inv[a_]] :> e, e :> Module[{a = Unique[]}, g[a, inv[a]]]}, g[x, y], 3, "CausalGraphInstances", MaxItems -> 8]](https://www.wolframcloud.com/obj/resourcesystem/images/f40/f404faf7-67a6-4fd2-a0a7-f80eebf7c4df/3303a83866978767.png)
|
| Out[73]= |
|
By default, "BranchPairsList" returns only a list of branch pairs:
| In[74]:= |
|
| Out[74]= |

|
Common predecessor states can be shown using "GivePredecessors":
| In[75]:= |
|
| Out[75]= |

|
Similarly, "BranchPairResolutionsList" by default lists only resolved and unresolved branch pairs:
| In[76]:= |
|
| Out[76]= |

|
Common resolvents of resolved branch pairs can be shown using "GiveResolvents":
| In[77]:= |
|
| Out[77]= |

|
Show both common predecessors and common resolvents, where appropriate:
| In[78]:= |
|
| Out[78]= |

|
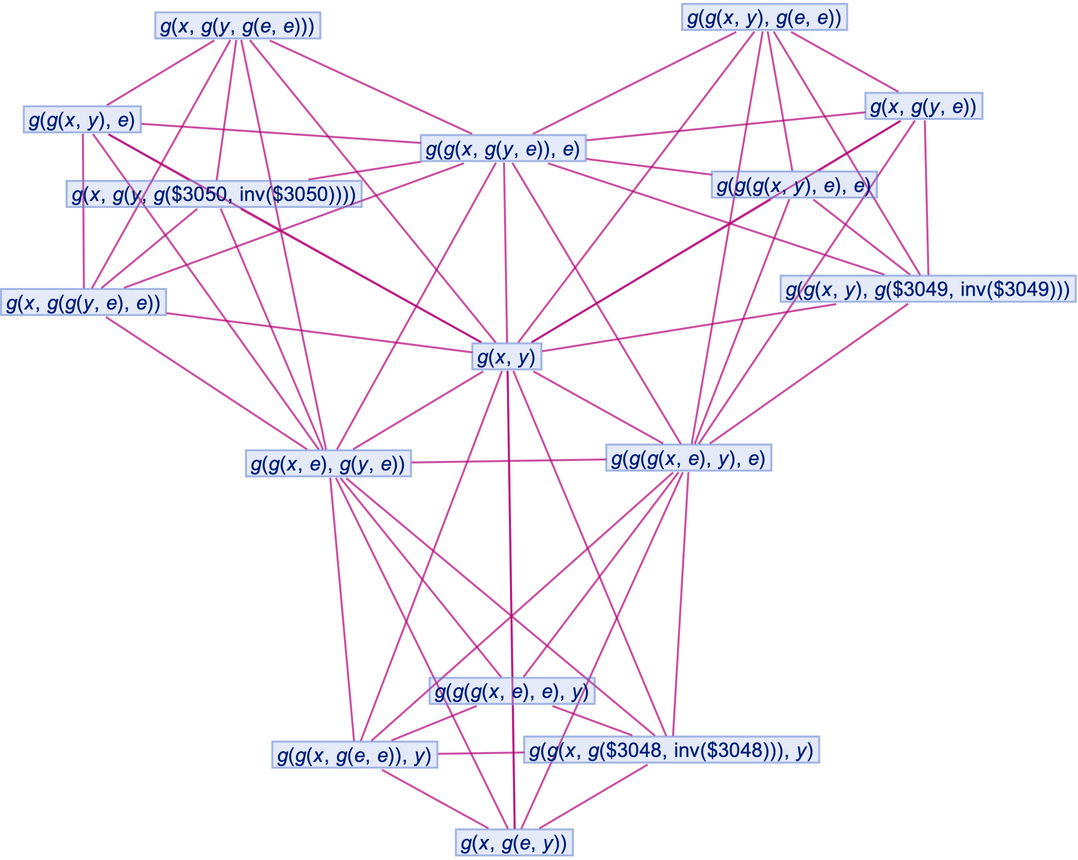
By default, non-branch pair states are not shown as part of the branchial graph:
| In[79]:= |
![ResourceFunction[
"MultiwayOperatorSystem"][{g[x_, g[y_, z_]] :> g[g[x, y], z], g[g[x_, y_], z_] :> g[x, g[y, z]], g[a_, e] :> a, a_ :> g[a, e], g[a_, inv[a_]] :> e, e :> Module[{a = Unique[]}, g[a, inv[a]]]}, g[x, y], 2, "BranchialGraph"]](https://www.wolframcloud.com/obj/resourcesystem/images/f40/f404faf7-67a6-4fd2-a0a7-f80eebf7c4df/785ecaa57943065f.png)
|
| Out[79]= |
|
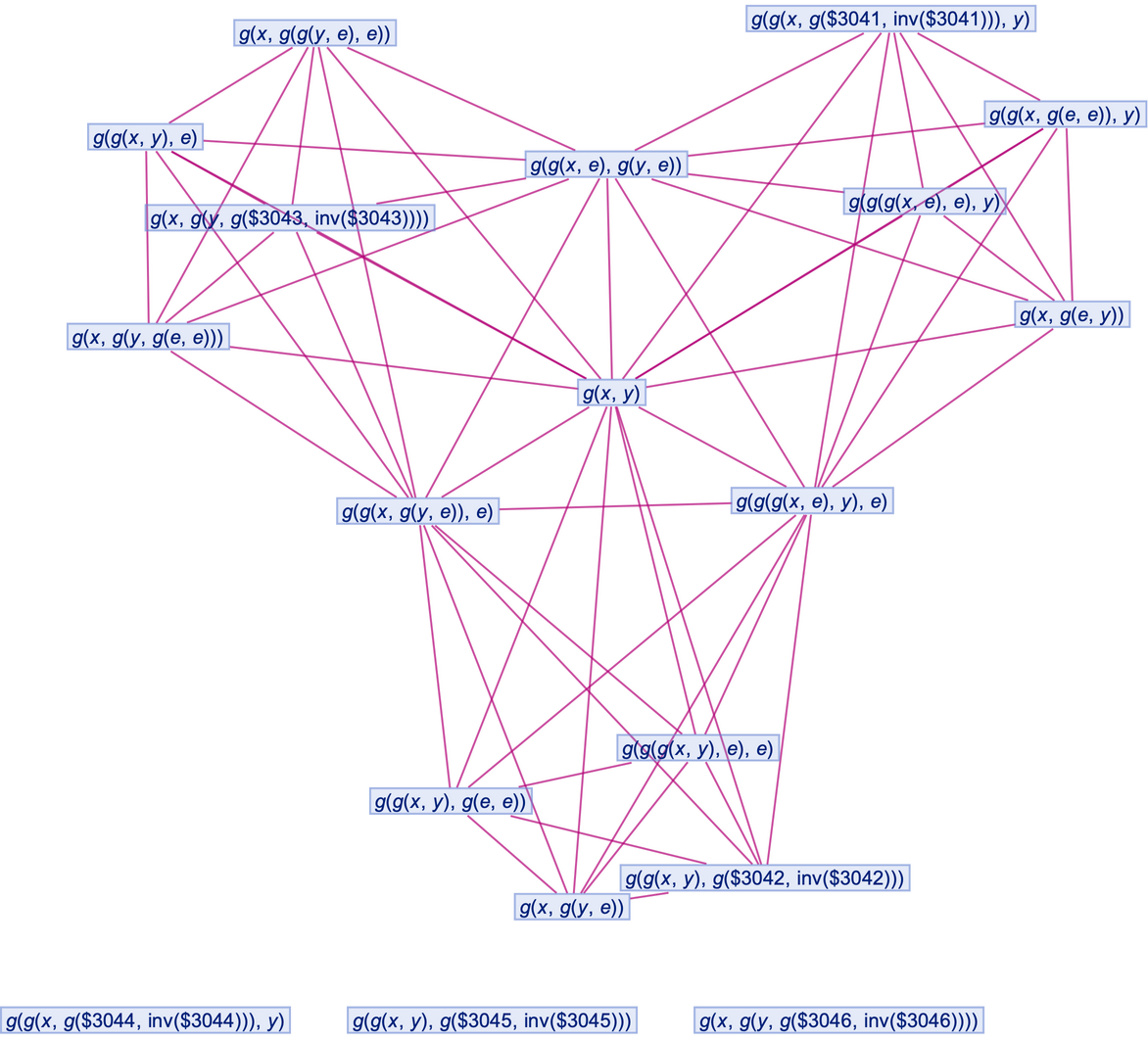
They can be shown by using "IncludeFullBranchialSpace":
| In[80]:= |
![ResourceFunction[
"MultiwayOperatorSystem"][{g[x_, g[y_, z_]] :> g[g[x, y], z], g[g[x_, y_], z_] :> g[x, g[y, z]], g[a_, e] :> a, a_ :> g[a, e], g[a_, inv[a_]] :> e, e :> Module[{a = Unique[]}, g[a, inv[a]]]}, g[x, y], 2, "BranchialGraph", "IncludeFullBranchialSpace" -> True]](https://www.wolframcloud.com/obj/resourcesystem/images/f40/f404faf7-67a6-4fd2-a0a7-f80eebf7c4df/7cb82451d0ac4c67.png)
|
| Out[80]= |
|
This work is licensed under a Creative Commons Attribution 4.0 International License