Wolfram Function Repository
Instant-use add-on functions for the Wolfram Language
Function Repository Resource:
Sort symbolic expressions using assumptions
ResourceFunction["SymbolicSort"][list,vars] attempts to sort list by assuming that the variables vars are real-valued. | |
ResourceFunction["SymbolicSort"][list,vars,assum] sorts by assuming that vars satisfy assumptions assum. | |
ResourceFunction["SymbolicSort"][list,vars,assum,dom] carries out symbolic manipulations over the domain dom. | |
Sort expressions in x defined for real numbers:
| In[1]:= |
| Out[1]= |
Plot to illustrate that Exp[x] is always greater than x:
| In[2]:= |
| Out[2]= | 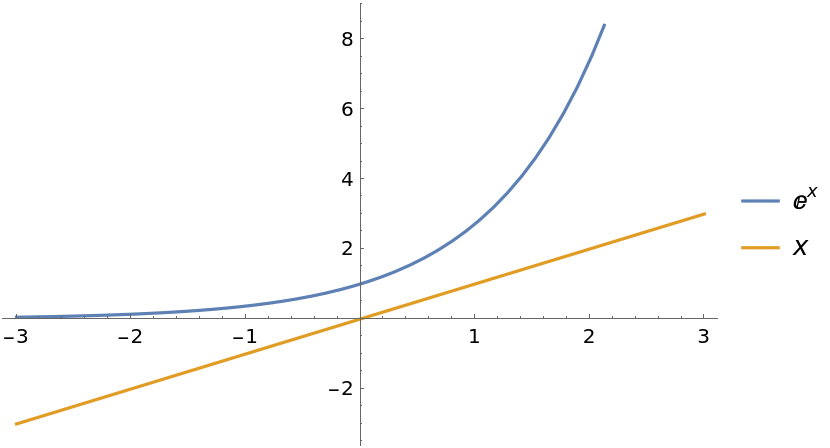 |
Use assumptions for sorting:
| In[3]:= |
| Out[3]= |
| In[4]:= |
| Out[4]= | 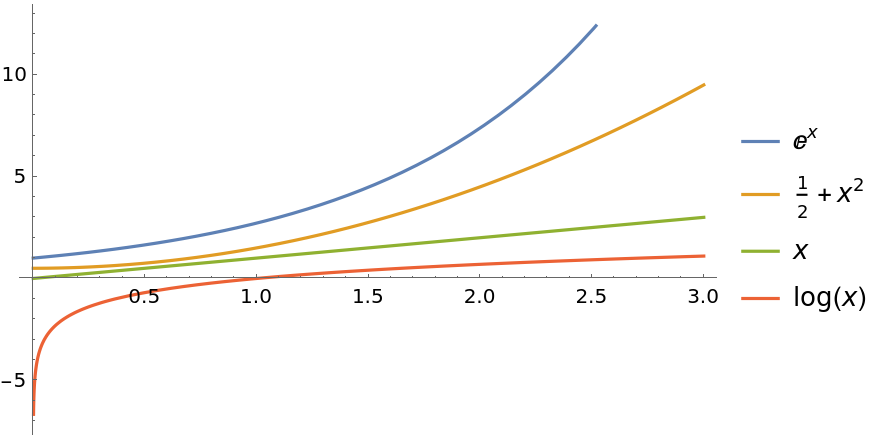 |
Sort expressions of a monotonic function applied to different variables:
| In[5]:= |
| Out[5]= |
If no definite order exists, a message will be raised and SymbolicSort remains unevaluated:
| In[6]:= |
| Out[6]= |
Use List as the last argument to force a result:
| In[7]:= |
| Out[7]= |
If not all expressions have a definite ordering, you can instead produce a Graph that shows the ordering relationships between the elements of the List:
| In[8]:= |
| Out[8]= |
| In[9]:= |
| Out[9]= | 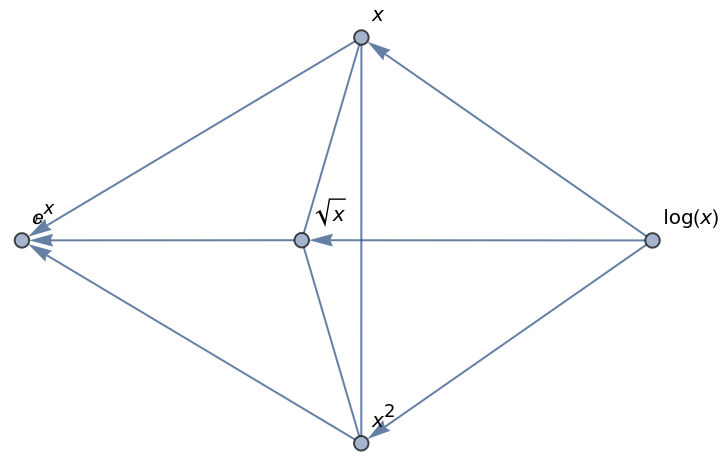 |
The undirected edges between ![]() , x and x2 show that these expressions have no definite ordering.
, x and x2 show that these expressions have no definite ordering.
A time constraint can be set for symbolic comparisons. If the time constraint is too low, no result will be found:
| In[10]:= |
| Out[10]= |
Sort the eigenvalues of a symbolic matrix:
| In[11]:= | ![ResourceFunction["SymbolicSort"][
Eigenvalues[{{a, 1}, {1, c}}],
{a, b, c},
0 < a < c,
Reals
]](https://www.wolframcloud.com/obj/resourcesystem/images/f3d/f3d4746e-86fb-4f09-a04f-abd0051acaab/6b2f54ed0be26ef6.png) |
| Out[11]= |
This work is licensed under a Creative Commons Attribution 4.0 International License