Wolfram Function Repository
Instant-use add-on functions for the Wolfram Language
Function Repository Resource:
Obtain the canonical bases for selected spaces of matrices and functions
ResourceFunction["CanonicalBasis"][type,var,degree] returns the canonical basis for polynomials or trigonometric polynomials of degree at most degree in the variable var. | |
ResourceFunction["CanonicalBasis"][type,size] returns the canonical basis for the space of matrices of type type and size size. |
| "DiagonalMatrices" |
| "HermitianMatrices" |
| "Matrices" |
| "Polynomials" |
| "SkewHermitianMatrices" |
| "SkewSymmetricMatrices" |
| "SymmetricMatrices" |
| "TraceZeroMatrices" |
| "TrigonometricPolynomials" |
The canonical basis for the space of polynomials in x of degree 5 or less:
| In[1]:= |
| Out[1]= |
The canonical basis for the space of 2×3 matrices:
| In[2]:= |
| Out[2]= |
The canonical basis for the space of trigonometric polynomials in x of degree 5 or less:
| In[3]:= |
| Out[3]= |
The canonical basis for the space of 3×3 square matrices:
| In[4]:= |
| Out[4]= |
The canonical basis for the space of 3×3 symmetric matrices:
| In[5]:= |
| Out[5]= |
The canonical basis for the space of 3×3 skew-symmetric matrices:
| In[6]:= |
| Out[6]= |
The Hermitian matrices of given degree do not form a vector space over the complex numbers, but they do form a vector space over the real numbers:
| In[7]:= |
| Out[7]= |
As with Hermitian matrices, the skew-Hermitian matrices of given degree form a vector space over the real numbers:
| In[8]:= |
| Out[8]= |
A Manipulate illustrating an array of function-related examples:
| In[9]:= | ![Manipulate[
ResourceFunction["CanonicalBasis"][type, x, degree], {type, {Polynomials, "TrigonometricPolynomials"}}, {degree,
Table[j, {j, 1, 10}]}]](https://www.wolframcloud.com/obj/resourcesystem/images/f3d/f3d42698-4f96-423b-874c-bada175cde7e/1a46c932a608fa12.png) |
| Out[9]= | 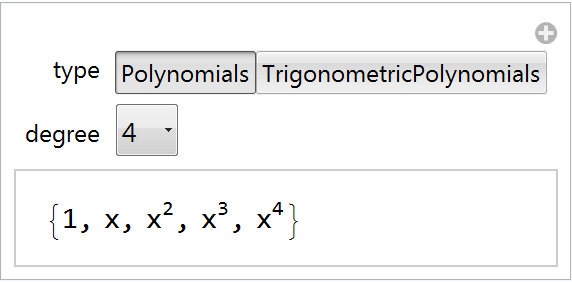 |
A Manipulate illustrating an array of matrix-theoretic examples:
| In[10]:= | ![Manipulate[
MatrixForm /@ ResourceFunction["CanonicalBasis"][type, size], {type, {"DiagonalMatrices", "HermitianMatrices", "SkewHermitianMatrices", "Matrices", "SymmetricMatrices", "SkewSymmetricMatrices", "TraceZeroMatrices"}}, {size, Range[2, 6]}]](https://www.wolframcloud.com/obj/resourcesystem/images/f3d/f3d42698-4f96-423b-874c-bada175cde7e/3624a294c6c25dad.png) |
| Out[10]= | 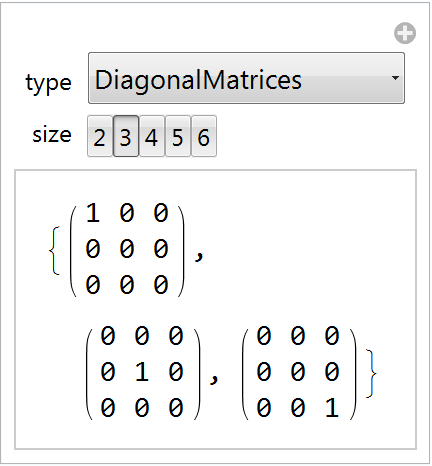 |
This work is licensed under a Creative Commons Attribution 4.0 International License