Function Repository Resource:

PolyhedronChop

Source Notebook

Remove duplicated graphical elements from a polyhedron

Contributed by: Ed Pegg Jr

ResourceFunction["PolyhedronChop"][poly]

merges near-identical points in the polyhedron poly, and then re-indexes based on the new point set.

Details

By convention for 3D printing, faces of a polyhedron have their vertices in counterclockwise order when viewed from the outside.

Examples

Basic Examples (3)

Clean up a messy polyhedron:

In[1]:=

messy = Polyhedron[CompressedData["
1:eJxtkktIm1EQhX8fVOtOcNVKIFZFE1KjKYhEOwsf+ESI4qLgRmpwIQqWFgUR
im2RIiaokSTFoKJmpYibKkTGVYKxlhKoILaoKKFihIgbQaU1/3+u0IsDd/Mx
nDP3zOg7em2dyYqimO9eyt3Ltjir/QMR/vEtUTG2ht88n974xRInwX2hpLyV
mUOOoL+paz82+IplToK3rEXT+xwbPOdJ1Bb7v6TZ37XGSeIkeKPKd0hRayWw
AD6t6sfBFWUA+nM+nd1nO+HX9kRFuQFzSpwEt6j65/QB81gf5vf/LQIfRT+B
m8An0S+4W5qzAXO6kE8YufWAezFnJ+Yvh04Z8v+O/pfgFeA70l680n9LwYWv
6P8M3xzk75Tyzwd3S/uqkfayCG4+2goN/z4lbY97nGP7+UJXH+Fi5PMVOkPx
8svb6DzlZyx9chl3yQFecU3Npt4zCged/e27roADOnXgT/DfbeRQCZ19VX/p
/m4L4Zu3rnHkRkbwp1Jug9Bpywx93Hy0HPBovlQFXzHnrLgH8BL8axW8Gzom
5LAInVz4+t9a/aOpf/jmb6IO2AA+gn29x96VC01Hr/nyBPKphu8z8Cn41oIL
nWHs/RrzCN8rzZcK4GtQdYLi3siof5w15j5mzTdK49Avkri4///7g9yB+Q3g
Xtxbsnonh2yWeJrGqRj8Hzuhbuk=
"], {{13, 14, 15}, {16, 17, 18}, {19, 20, 21}, {22, 23, 24}, {25, 26, 27, 28, 29, 30}, {31, 32, 33, 34, 35, 36}, {37, 38, 39, 40, 41, 42}, {43, 44, 45, 46, 47, 48}, {30, 29, 3, 16, 18, 1}, {47, 46, 1,
18, 17, 9}, {46, 45, 11, 25, 30, 1}, {32, 31, 2, 19, 21, 4}, {43,
48, 10, 20, 19, 2}, {44, 43, 2, 31, 36, 12}, {39, 38, 3, 29, 28, 5}, {38, 37, 9, 17, 16, 3}, {41, 40, 6, 33, 32, 4}, {42, 41, 4, 21, 20, 10}, {40, 39, 5, 23, 22, 6}, {28, 27, 7, 24, 23, 5}, {34, 33, 6, 22, 24, 7}, {35, 34, 7, 27, 26, 8}, {26, 25, 11, 13, 15, 8}, {36, 35, 8, 15, 14, 12}, {48, 47, 9, 37, 42, 10}, {45, 44, 12,
14, 13, 11}}];
clean = ResourceFunction["PolyhedronChop"][messy]

Out[1]=

The returned object is now a simple polyhedron:

In[2]:=

Out[2]=

As an aid for 3D printing formats, all faces have the same orientation:

In[3]:=

Out[3]=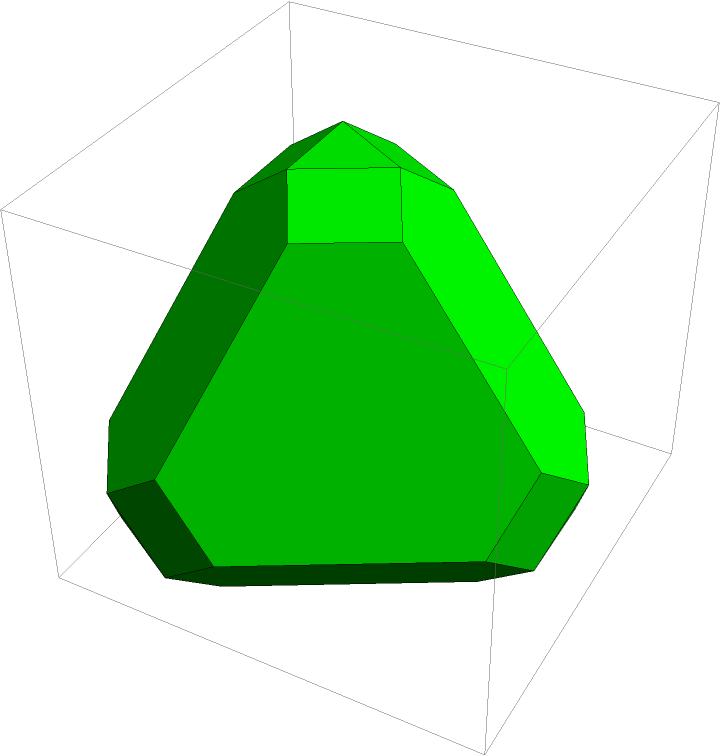

Scope (2)

Variations on 2 and -2 lead to a messy tetrahedron with 108 vertices and 78732 faces:

In[4]:=

$twovalues = {-2, -2., 2, 2., -2/GoldenRatio^2 - 2/GoldenRatio, 1/GoldenRatio^2 + GoldenRatio}; v = Union[Select[Tuples[twovalues, {3}], Times @@ N[#] > 0 &]]; f = Quiet@ Select[Subsets[Range[Length[v]], {3}], Min[EuclideanDistance @@ v[[#]] & /@ Subsets[#, {2}]] > 1 &]; messytetra = Polyhedron[v, f]$

Out[4]=

PolyhedronChop cleans up the messiness:

In[5]:=

Out[5]=

Faces appear in counterclockwise orientation when viewed from the outside:

In[6]:=

Out[6]=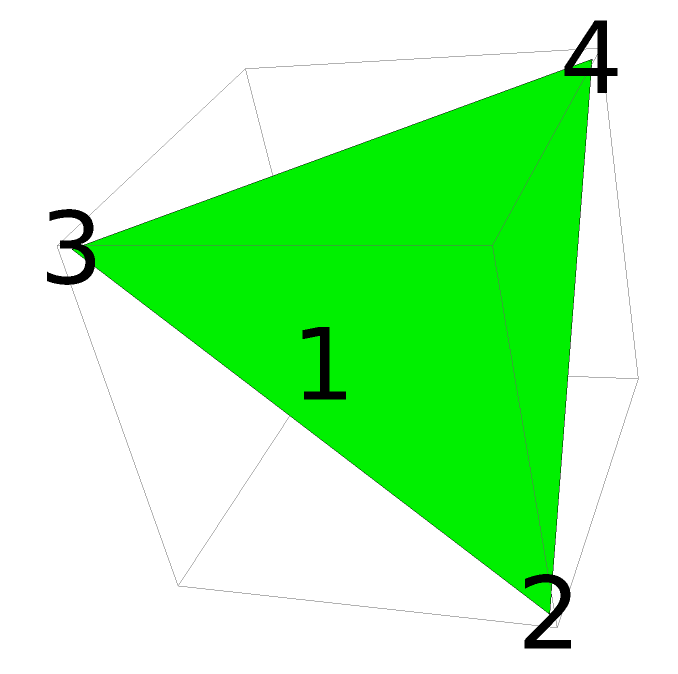

A polyhedron with different face orientations often cannot be 3D printed:

In[7]:=

tsi = Polyhedron[{{-1, GoldenRatio, 0}, {1, GoldenRatio, 0}, {-1, -GoldenRatio, 0}, {1, -GoldenRatio, 0}, {0, 1, -GoldenRatio}, {0, -1, -GoldenRatio}, {0, 1, GoldenRatio}, {0, -1, GoldenRatio}, {-GoldenRatio, 0, -1}, {-GoldenRatio, 0, 1}, {GoldenRatio, 0, -1}, {GoldenRatio,
0, 1}, {Rational[1, 5] (1 + 3 GoldenRatio), Rational[1, 5] (1 + 3 GoldenRatio), Rational[1, 5] (1 + 3 GoldenRatio)}, {Rational[1, 5] (
1 + 3 GoldenRatio), Rational[1, 5] (-1 - 3 GoldenRatio), Rational[1, 5] (-1 - 3 GoldenRatio)}, {Rational[
1, 5] (-1 - 3 GoldenRatio), Rational[1, 5] (1 + 3 GoldenRatio), Rational[1, 5] (-1 - 3 GoldenRatio)}, {Rational[
1, 5] (-1 - 3 GoldenRatio), Rational[1, 5] (-1 - 3 GoldenRatio),
Rational[1, 5] (1 + 3 GoldenRatio)}}, {{1, 2, 5, 15}, {1, 7, 13,
2}, {3, 4, 14, 6}, {3, 4, 8, 16}, {5, 6, 9, 15}, {5, 6, 14, 11}, {7, 8, 16, 10}, {7, 8, 12, 13}, {9, 10, 1, 15}, {9, 10, 16, 3}, {11, 12, 13, 2}, {11, 12, 4, 14}, {1, 7, 10}, {2, 5, 11}, {3, 6, 9}, {4, 8, 12}}];
Graphics3D[{FaceForm[Green, Red], tsi}]

Out[7]=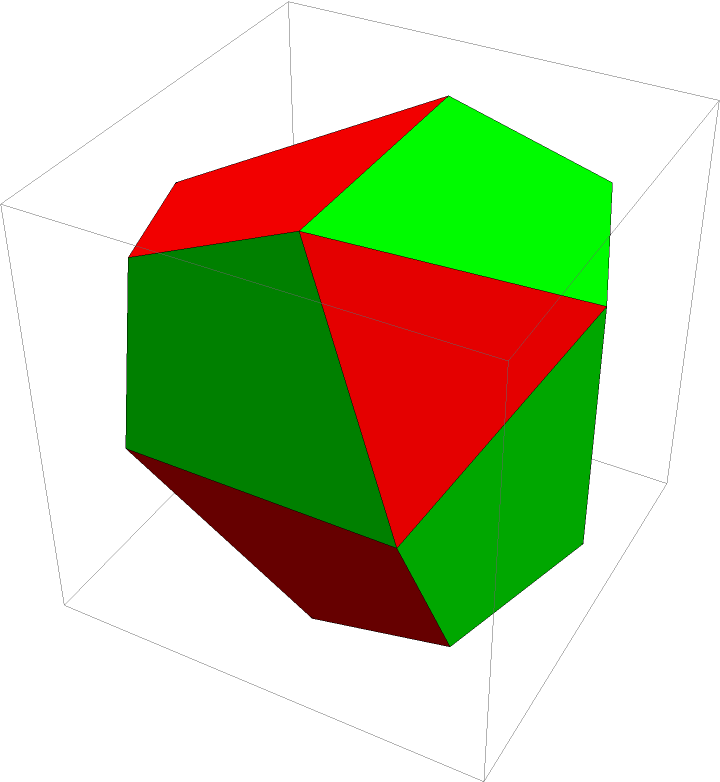

PolyhedronChop returns consistent face orientations:

In[8]:=

Out[8]=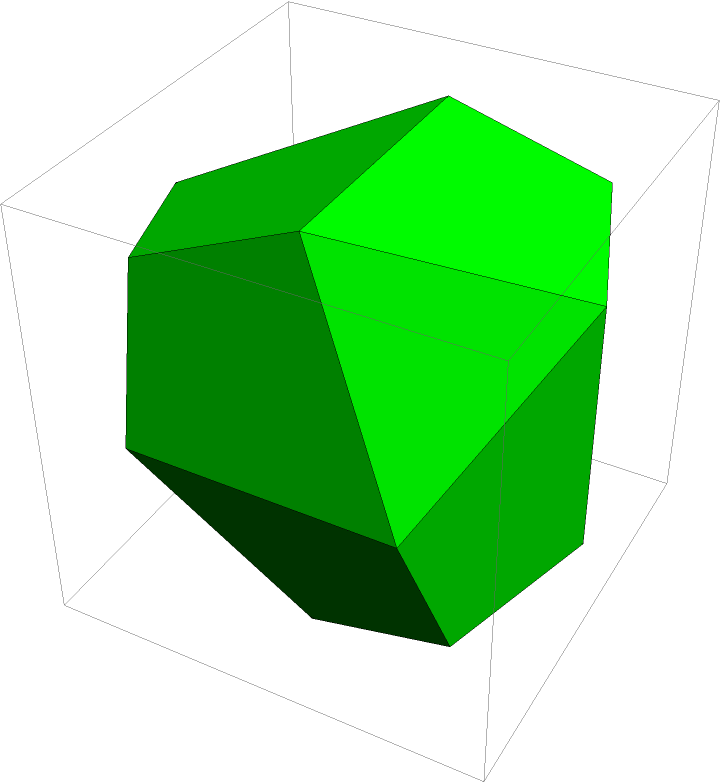

Possible Issues (2)

Objects in PolyhedronData have consistent face orientations:

In[9]:=

Out[9]=

PolyhedronChop may return faces in a different but equivalent form:

In[10]:=

Out[10]=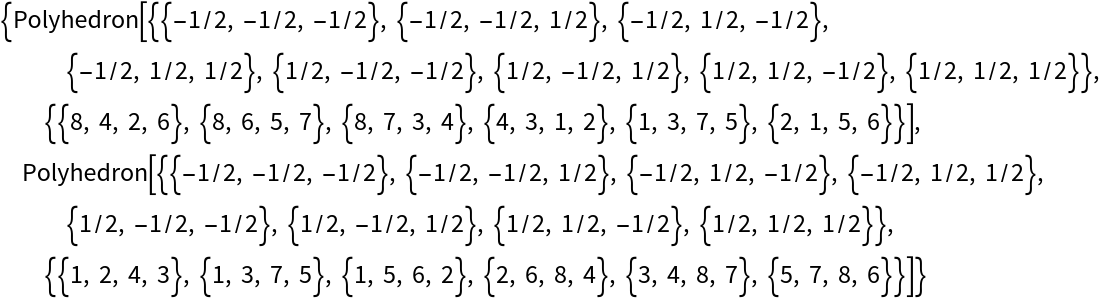

Version History

1.0.0 – 20 September 2021

Related Resources

License Information

This work is licensed under a Creative Commons Attribution 4.0 International License