Basic Examples (3) 

Generate a rotation matrix from its axis-angle representation:

In[1]:=

Out[1]=

Reconstitute the axis-angle representation from the matrix:

In[2]:=

Out[2]=

Use Activate to see the matrix again:

In[3]:=

Out[3]=

Scope (3) 

A real matrix:

In[4]:=

Out[4]=

Its axis-angle:

In[5]:=

Out[5]=

An approximate MachinePrecision matrix:

In[6]:=

Out[6]=

Its axis-angle:

In[7]:=

Out[7]=

An approximate arbitrary precision matrix:

In[8]:=

Out[8]=

Its axis-angle:

In[9]:=

Out[9]=

Applications (3) 

Generate a matrix from a given set of Euler angles:

In[10]:=

Out[10]=

Convert to its axis-angle representation:

In[11]:=

Out[11]=

Verify that they give the same rotation matrix:

In[12]:=

Out[12]=

Generate a matrix from a given set of roll-pitch-yaw angles:

In[13]:=

Out[13]=

Convert to its axis-angle representation:

In[14]:=

Out[14]=

Verify that they give the same rotation matrix:

In[15]:=

Out[15]=

Generate a random rotation matrix:

In[16]:=

Out[16]=

Convert to its axis-angle representation:

In[17]:=

Out[17]=

Properties and Relations (1) 

AxisAngle is effectively the inverse of RotationMatrix:

In[18]:=

In[19]:=

Out[19]=

In[20]:=

Out[20]=

Possible Issues (1) 

For singular rotation matrices, the choice of axis returned is arbitrary:

In[21]:=

Out[21]=

In[22]:=

Out[22]=

In[23]:=

Out[23]=

In[24]:=

Out[24]=

Neat Examples (2) 

Generate two random unit vectors:

In[25]:=

Out[25]=

Find the axis-angle representation of the matrix that transforms one vector to the other:

In[26]:=

Out[26]=

Verify the result:

In[27]:=

Out[27]=

In[28]:=

Out[28]=

In[29]:=

Out[29]=

Here are two polygons:

In[30]:=

Use FindGeometricTransform to find a rigid transformation between the two:

In[31]:=

Out[31]=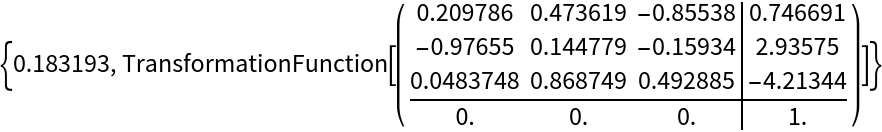

Extract the rotation matrix:

In[32]:=

Out[32]=

Convert the rotation matrix to its axis-angle representation:

In[33]:=

Out[33]=