Wolfram Function Repository

Instant-use add-on functions for the Wolfram Language

Function Repository Resource:

 EulerPhiInverse

Source Notebook

Get the list of integers whose Euler totients are equal to a given value

Contributed by: Shenghui Yang

ResourceFunction["EulerPhiInverse"][n]

lists the integers m such that EulerPhi[m]=n.

ResourceFunction["EulerPhiInverse"][n,k]

lists the integers m such that EulerPhi[m]= n up to k terms.

Details

The default value of k is 10000.
The inverse of Euler totient function ϕ-1 returns an empty list for all odd number except 1.
Even though all nontrivial totients are even, the converse does not hold. Some even numbers, called non-totients, have no preimage under Euler's totient function.
The inverse of the Euler totient function for any given n is bounded. ResourceFunction["EulerPhiInverse"] tries to find all solutions.
This function handles large input efficiently.

Examples

Basic Examples (2) 

Find all integers m such that ϕ(m)=1000:

In[1]:=
ResourceFunction["EulerPhiInverse"][1000]
Out[1]=

Check:

In[2]:=
EulerPhi /@ {1111, 1255, 1375, 1875, 2008, 2222, 2500, 2510, 2750, 3012, 3750}
Out[2]=

Scope (2) 

Find all 6535 integers m such that ϕ(m)=1020:

In[3]:=
(data = ResourceFunction["EulerPhiInverse"][10^20];) // AbsoluteTiming
Out[3]=
In[4]:=
Length[data]
Out[4]=
In[5]:=
data // Short
Out[5]=

Verify that these are the correct solutions:

In[6]:=
Log10@EulerPhi[RandomSample[data, 20]]
Out[6]=

It takes only a fraction of second to find all solution for the numbers below on a modern computer:

In[7]:=
AbsoluteTiming[ ResourceFunction["EulerPhiInverse"][ 2^3 31^3 313^3 619^3 1511^3 1733^3]]
Out[7]=
In[8]:=
ResourceFunction["EulerPhiInverse"][2^5*3^5*5^5] // Length // AbsoluteTiming
Out[8]=

Properties and Relations (2) 

EulerPhiInverse returns an empty list for all odd integer except 1:

In[9]:=
ResourceFunction["EulerPhiInverse"] /@ {1, 3, 5, 7, 9, 11}
Out[9]=

List non-totients:

In[10]:=
ResourceFunction["OEISSequenceData"]["A005277"]
Out[10]=

Show that non-totients have no preimage under Euler's totient function:

In[11]:=
ResourceFunction["EulerPhiInverse"] /@ %
Out[11]=

Possible Issues (2) 

EulerPhiInverse only handles positive integers. Otherwise, it returns unevaluated:

In[12]:=
ResourceFunction["EulerPhiInverse"][0.3]
Out[12]=

The number of solutions may grow rapidly for those inputs with prime factors p such that p-1 is highly composite:

In[13]:=
ResourceFunction["EulerPhiInverse"][10^22] // Short
Out[13]=

Increase the second argument to get all solutions for x such that EulerPhi[x]=1028:

In[14]:=
ResourceFunction["EulerPhiInverse"][10^22, 2*10^4] // Length
Out[14]=

Neat Examples (3) 

Numbers k such that EulerPhi[x]=k has exactly 2 solutions (OEIS A007366):

In[15]:=
seq = Select[Table[i, {i, 2, 1000, 2}], With[{b = Length[ResourceFunction["EulerPhiInverse"][#]]}, b == 2] &]; Short[seq]
Out[16]=
In[17]:=
ResourceFunction["OEISLookup"]@(seq[[;; 10]])
Out[17]=

Visualize the data:

In[18]:=
ListPlot[data]
Out[18]=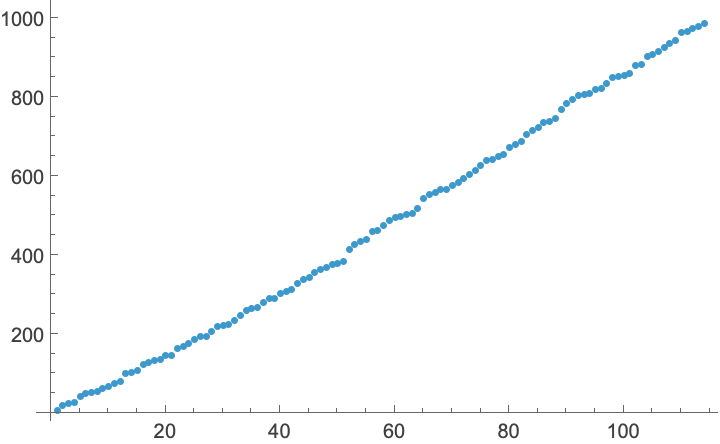

A pair of dual graph: n→ϕ(n) on the right and n→ m for ϕ(m) =n on the left:

In[19]:=
g1 = Graph[ Table[With[{epi = ResourceFunction["EulerPhiInverse"][i]}, If[epi != {}, i -> # & /@ epi, Nothing]], {i, 2, 500, 2}] // Flatten]; g2 = Graph[Table[i -> EulerPhi[i], {i, 2, 500}]]; GraphicsGrid[{{g1, g2}}]
Out[20]=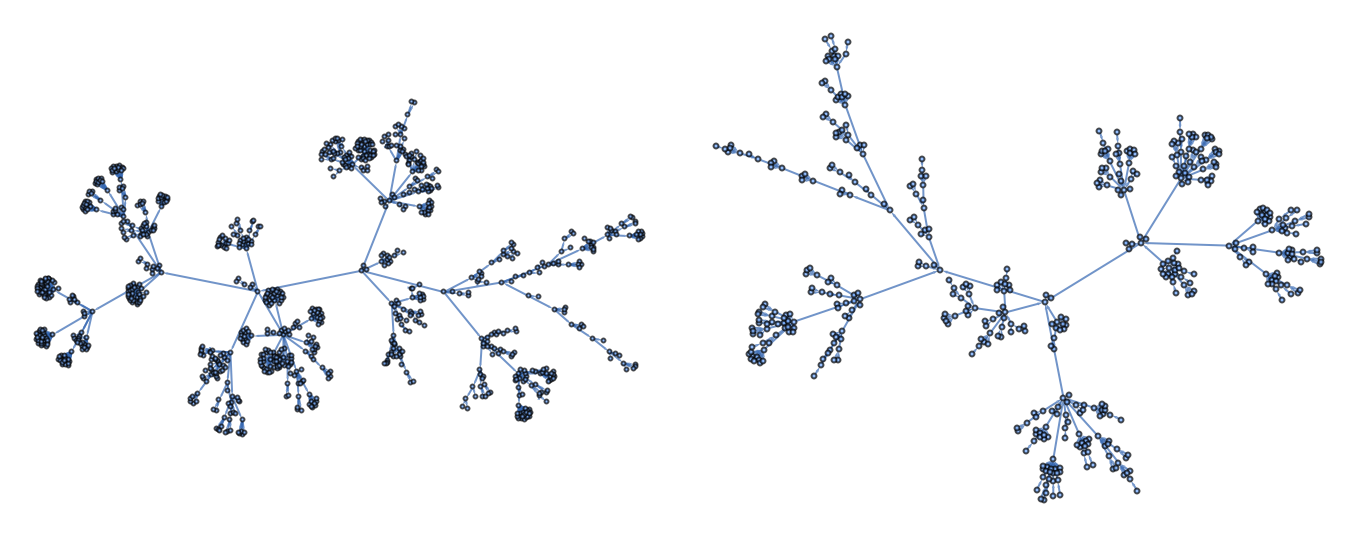

The graph on the left hand side seems denser than the right because the inverse of ϕ is a multivalued function:

In[21]:=
{VertexCount[g1], VertexCount[g2]}
Out[21]=

Number of integers k such that EulerPhi[k]=n (OEIS A072074):

In[22]:=
seq = ParallelMap[ResourceFunction["EulerPhiInverse"], (10^Range[20])]; seq = Length /@ seq
Out[23]=
In[24]:=
ResourceFunction["OEISLookup"]@seq
Out[24]=

Plot the data and its logarithm approximation:

In[25]:=
fit = Fit[Log@seq, {1, \[FormalX]}, \[FormalX]];
In[26]:=
Show[ListLogPlot[seq], Plot[fit, {\[FormalX], 0, 20}, PlotStyle -> Dashed]]
Out[26]=

Publisher

Shenghui Yang

Requirements

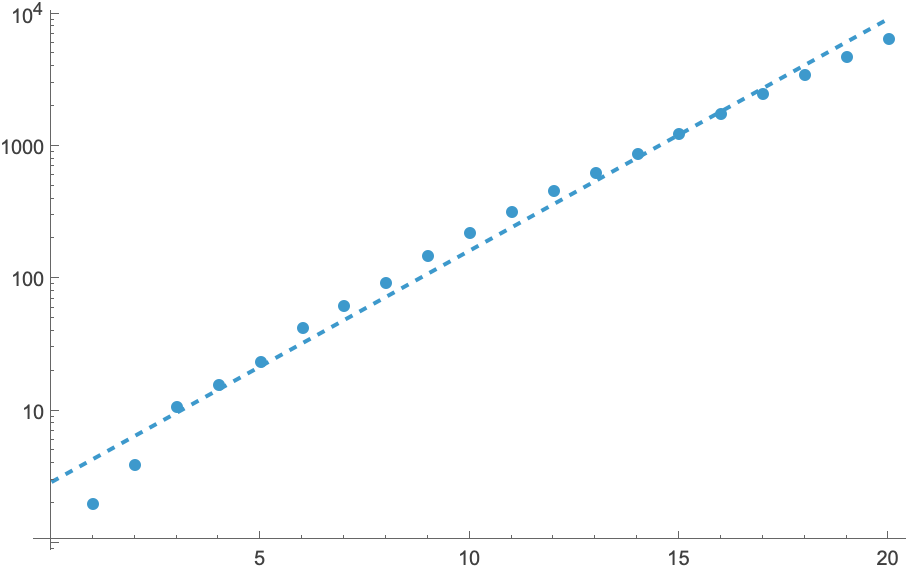Wolfram Language 13.0 (December 2021) or above

Version History

  • 1.0.1 – 15 October 2025
  • 1.0.0 – 06 October 2025

Source Metadata

Related Resources

License Information