Wolfram Function Repository

Instant-use add-on functions for the Wolfram Language

Function Repository Resource:

 IdentityTensorReduce

Source Notebook

Simplify expressions containing a symbolic identity tensor

Contributed by: Carl Woll

ResourceFunction["IdentityTensorReduce"][expr]

converts TensorContract expressions containing symbolic identity tensors into equivalent forms with the identity tensors removed.

Details and Options

ResourceFunction["IdentityTensorReduce"] makes no assumptions about the rank of the symbolic tensors involved. Use the Assumptions option or $Assumptions to define rank information for the involved tensors.
The input and output of ResourceFunction["IdentityTensorReduce"] will evaluate to the same array when given explicit arrays as input.

Examples

Basic Examples (2) 

A simple tensor contraction of a tensor with an identity matrix:

In[1]:=
e = TensorContract[TensorProduct[X, IdentityMatrix[n]], {{2, 3}}]
Out[1]=

TensorReduce does not simplify the tensor:

In[2]:=
TensorReduce[e, Assumptions -> X \[Element] Matrices[{n, n}]]
Out[2]=

IdentityTensorReduce simplifies the tensor:

In[3]:=
ResourceFunction["IdentityTensorReduce"][e, Assumptions -> X \[Element] Matrices[{n, n}]]
Out[3]=

Use Inactive when the dimensions of the identity tensor are explicit:

In[4]:=
e = TensorContract[ TensorProduct[X, Inactive[IdentityMatrix][3], X], {{2, 3}, {4, 6}}]
Out[4]=

IdentityTensorReduce simplifies the tensor:

In[5]:=
ResourceFunction["IdentityTensorReduce"][e, Assumptions -> X \[Element] Matrices[{n, n}]]
Out[5]=

Scope (6) 

Define assumptions for a matrix X and scalars a, b and c:

In[6]:=
$Assumptions = X \[Element] Matrices[{n, n}] && (a | b | c) \[Element] Reals;

A tensor expression involving the identity tensor:

In[7]:=
t = a TensorProduct[IdentityMatrix[n], IdentityMatrix[n]] + b TensorTranspose[ TensorProduct[IdentityMatrix[n], IdentityMatrix[n]], {1, 3, 2, 4}] + c TensorTranspose[ TensorProduct[IdentityMatrix[n], IdentityMatrix[n]], {1, 3, 4, 2}]
Out[7]=

Contract this tensor with another tensor:

In[8]:=
e = TensorContract[TensorProduct[X, t, X], {{1, 8}, {2, 3}, {6, 7}}]
Out[8]=

Expand the tensor into a sum of tensors:

In[9]:=
s = TensorExpand[e]
Out[9]=

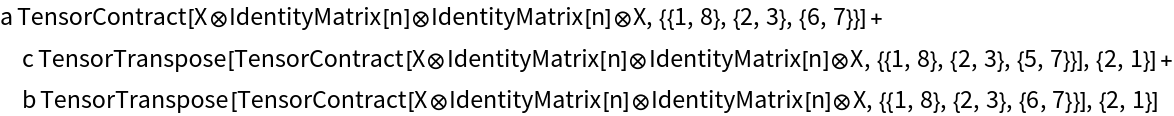Use IdentityTensorReduce to eliminate contracted identity tensors:

In[10]:=
r = ResourceFunction["IdentityTensorReduce"][s]
Out[10]=

The ResourceFunction "FromTensor" can be used to rewrite this expression in terms of Dot:

In[11]:=
ResourceFunction["FromTensor"][r]
Out[11]=

Publisher

Carl Woll

Version History

  • 1.0.0 – 09 November 2020

Related Resources

License Information