Wolfram Function Repository

Instant-use add-on functions for the Wolfram Language

Function Repository Resource:

 LeibnizHarmonicTriangle

Source Notebook

Display a given number of rows in the Leibniz harmonic triangle

Contributed by: Shenghui Yang

ResourceFunction["LeibnizHarmonicTriangle"][n]

creates a two level table representing the first n rows of Leibniz's harmonic triangle.

ResourceFunction["LeibnizHarmonicTriangle"][r,c]

returns the c-th element in the r-th row of the triangle.

Details

LeibnizHarmonicTriangle uses the integral definition associated with the Beta function. Specifically, the c-th element in the r-th row of the Leibniz harmonic triangle is .
In general, the terms have the recurrence relation: L(r,1)=1/r, L(r,c)=L(r-1,c-1)-L(r,c-1) for c>1.
In ResourceFunction["LeibnizHarmonicTriangle"][r,c], r and c must be positive integers with 1<=c<=r.

Examples

Basic Examples (2) 

Display the first five rows of Leibniz's triangle:

In[1]:=
lt = ResourceFunction[ "LeibnizHarmonicTriangle", ResourceSystemBase -> "https://www.wolframcloud.com/obj/resourcesystem/api/1.0"][5]
Out[1]=

Show them as a triangle:

In[2]:=
Column[Grid[{#}, ItemSize -> 3] & /@ (lt /. x_?NumericQ :> Text[Style[x, Large]]), Center]
Out[2]=

Properties and Relations (3) 

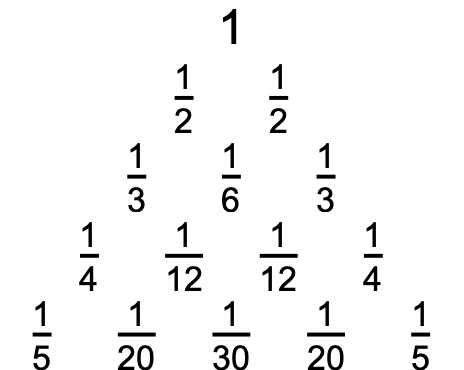Reverse hockey-stick property: the blue number 1/3 equals the infinite sum of the numbers along the orange line or the 4th diagonal:

In[3]:=
lt = ResourceFunction[ "LeibnizHarmonicTriangle", ResourceSystemBase -> "https://www.wolframcloud.com/obj/resourcesystem/api/1.0"][12] /. x_?NumericQ :> Text[Style[x, 18, FontFamily -> "Helvetica"]];
In[4]:=
colorBand[list_, idx_Integer, col_RGBColor] := Module[{updated = list}, updated[[idx]] = Style[list[[idx]], 18, col, FontFamily -> "Helvetica", Background -> LightBlue]; updated]
In[5]:=
Column[Grid[{#}, ItemSize -> 3] & /@ Prepend[ colorBand[#, 4, Orange] & /@ (lt[[4 ;;]]), Splice[lt[[{1, 2}]]~Join~{colorBand[lt[[3]], 3, Blue]}] ], Center]
Out[5]=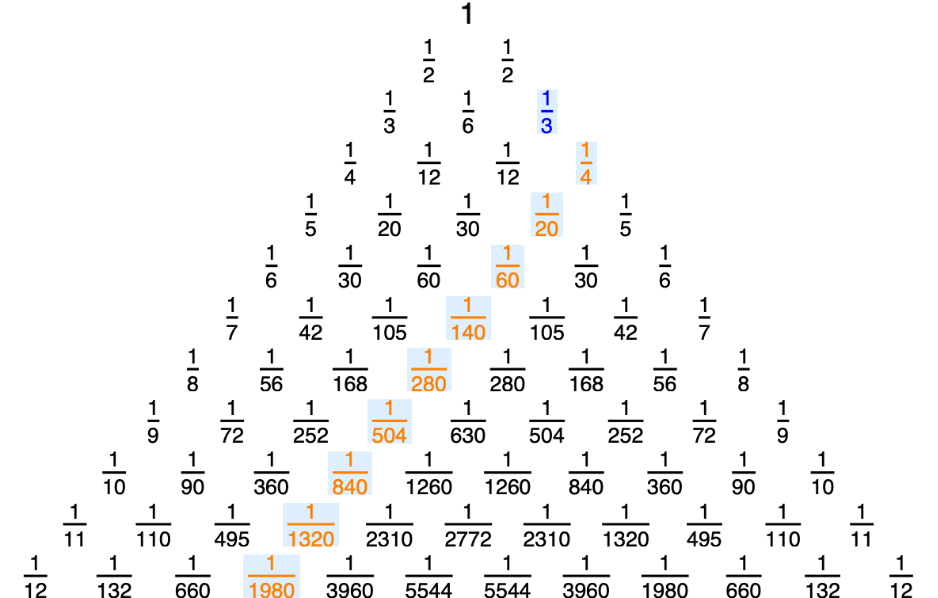

Verify with symbolic summation with the definition of Leibniz triangle by built-in Beta function:

In[6]:=
Sum[Beta[4, r + 1 - 4], {r, 4, Infinity}]
Out[6]=

In general the infinite sum along c-th column is L(c-1,c-1):

In[7]:=
Table[Sum[ ResourceFunction[ "LeibnizHarmonicTriangle", ResourceSystemBase -> "https://www.wolframcloud.com/obj/resourcesystem/api/1.0"][r, c], {r, c, Infinity}], {c, 3, 10}]
Out[7]=
In[8]:=
Array[ResourceFunction[ "LeibnizHarmonicTriangle", ResourceSystemBase -> "https://www.wolframcloud.com/obj/resourcesystem/api/1.0"][# - 1, # - 1] &, 8, 3]
Out[8]=

The sum of denominators in r-th row is r·2r-1:

In[9]:=
lt = ResourceFunction[ "LeibnizHarmonicTriangle", ResourceSystemBase -> "https://www.wolframcloud.com/obj/resourcesystem/api/1.0"][12];
In[10]:=
Total@*Denominator /@ lt
Out[10]=
In[11]:=
Array[#*2^(# - 1) &, 12]
Out[11]=

The Leibniz harmonic triangle is related to binomial triangle:

In[12]:=
TraditionalForm[1/Binomial[n, m]/(n + 1)]
Out[12]=
In[13]:=
Table[1/Binomial[n, m]/(n + 1), {n, 0, 5}, {m, 0, n}]
Out[13]=
In[14]:=
ResourceFunction[ "LeibnizHarmonicTriangle", ResourceSystemBase -> "https://www.wolframcloud.com/obj/resourcesystem/api/1.0"][6]
Out[14]=

Neat Examples (3) 

The original Sierpiński triangle pattern:

In[15]:=
lt = ParallelMap[Boole[ResourceFunction["FractionMod"][#, 8] == 0] &, ResourceFunction[ "LeibnizHarmonicTriangle", ResourceSystemBase -> "https://www.wolframcloud.com/obj/resourcesystem/api/1.0"][500], {2}];
In[16]:=
ArrayPlot[PadRight[#, 500] & /@ lt]
Out[16]=

Sierpiński triangle using fraction mod 3:

In[17]:=
lt = ParallelMap[ResourceFunction["FractionMod"][#, 3] &, ResourceFunction[ "LeibnizHarmonicTriangle", ResourceSystemBase -> "https://www.wolframcloud.com/obj/resourcesystem/api/1.0"][500], {2}]; ArrayPlot[PadRight[#, 500] & /@ lt]
Out[18]=

Sierpiński triangle using fraction mod 5:

In[19]:=
lt = ParallelMap[ResourceFunction["FractionMod"][#, 5] &, ResourceFunction[ "LeibnizHarmonicTriangle", ResourceSystemBase -> "https://www.wolframcloud.com/obj/resourcesystem/api/1.0"][600], {2}]; ArrayPlot[PadRight[#, 600] & /@ lt]
Out[20]=

Publisher

Shenghui Yang

Requirements

Wolfram Language 14.0 (January 2024) or above

Version History

  • 1.0.0 – 12 November 2024

Source Metadata

Related Resources

Author Notes

The fractal pattern in the neat examples might be a discovery of association between Sierpiński triangle and Leibniz triangle.

License Information