Wolfram Function Repository
Instant-use add-on functions for the Wolfram Language
Function Repository Resource:
Bootstrap a single statistic or a list of statistics
ResourceFunction["BootstrapStatistics"][data,n] returns a list of n bootstrapped datasets. | |
ResourceFunction["BootstrapStatistics"][data,n,func] returns a list of the values of func applied to n bootstrapped datasets. | |
ResourceFunction["BootstrapStatistics"][data,n,funclist] returns a list each function in funclist applied to n bootstrapped datasets. |
Create five bootstrapped datasets by resampling from an original dataset:
| In[1]:= |
| Out[1]= |
Compute the Mean of a dataset:
| In[2]:= |
| Out[2]= |
Compare it to the means of ten bootstrapped samples:
| In[3]:= |
| Out[3]= | 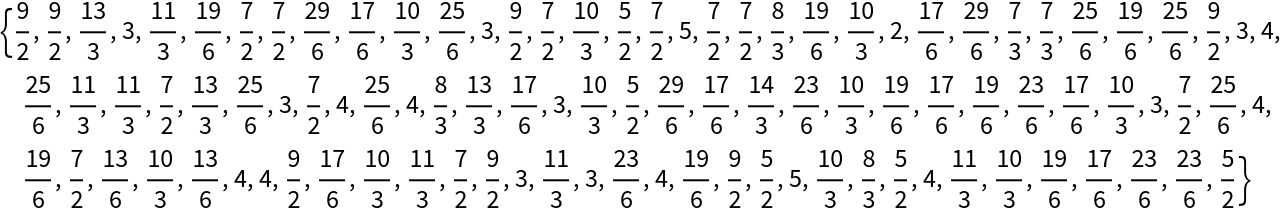 |
| In[4]:= |
| Out[4]= | 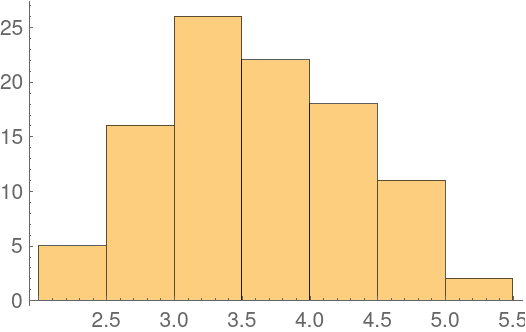 |
Pass a list of functions to BootstrapStatistics to get a list of lists of results:
| In[5]:= |
| Out[5]= |
The example dataset "BuffaloSnow" shows snowfall records for Buffalo, New York:
| In[6]:= |
| Out[6]= |
With traditional methods, we can only get one estimate for the mean snowfall:
| In[7]:= |
| Out[8]= |
Using the bootstrap method, we can get a larger set giving us a better idea of how much this measure varies:
| In[9]:= |
| Out[10]= | 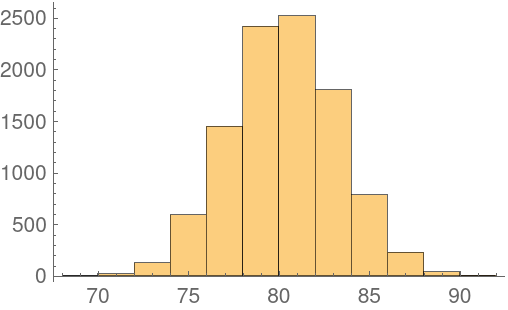 |
We can use Quantile to find the 95% confidence interval:
| In[11]:= |
| Out[11]= |
This work is licensed under a Creative Commons Attribution 4.0 International License