Wolfram Function Repository

Instant-use add-on functions for the Wolfram Language

Function Repository Resource:

 FindEquationalCounterexample

Source Notebook

Try to find a counterexample to an equational hypothesis in a given system of axioms

Contributed by: Jonathan Gorard

ResourceFunction["FindEquationalCounterexample"][hyp,axms]

tries to find an equational counterexample to the symbolic hypotheses hyp using the axioms axms.

Details and Options

If ResourceFunction["FindEquationalCounterexample"][hyp,axms] succeeds in finding a counterexample to the hypotheses hyp given the axioms axms, then it returns a CounterexampleObject expression.
Axioms and hypotheses must be given in equational form.
The inputs hyp and axms can be any logical combination of terms of the form:
expr1⩵expr2assertion of equality
ForAll[vars,stmt]assertion that stmt is true for all values of vars
The expri can be arbitrary symbolic expressions, with heads representing formal operators, functions etc.
ResourceFunction["FindEquationalCounterexample"][expr1&&expr2&&…,axm1&&axm2&&…] will treat each expri as a separate hypothesis and each axmi as a separate axiom.
ResourceFunction["FindEquationalCounterexample"][{expr1,expr2,…},{axm1,axm2,…}] is equivalent to ResourceFunction["FindEquationalCounterexample"][expr1&&expr2&&…,axm1&&axm2&&…].
ResourceFunction["FindEquationalCounterexample"] uses the back end of FindEquationalProof to find an appropriate counterexample to the hypothesis.

Examples

Basic Examples (2) 

Find a counterexample to an elementary hypothesis in group theory:

In[1]:=
counterexample = ResourceFunction["FindEquationalCounterexample"][ ForAll[a, g[a, e] == e], {ForAll[{a, b, c}, g[a, g[b, c]] == g[g[a, b], c]], ForAll[a, g[a, e] == a], ForAll[a, g[a, inv[a]] == e]}]
Out[1]=

Show the counterexample association:

In[2]:=
counterexample["CounterexampleAssociation"]
Out[2]=

Generate a function to verify that this is a valid counterexample to the hypothesis:

In[3]:=
counterexample["FalsificationFunction"]
Out[3]=
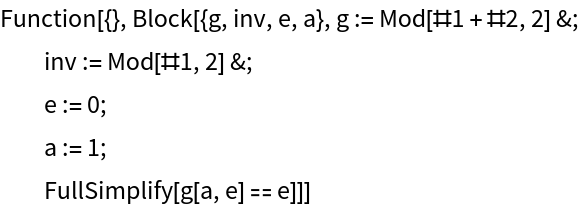
In[4]:=
%[]
Out[4]=

Generate a function to verify that this counterexample is consistent with the underlying axioms:

In[5]:=
counterexample["VerificationFunction"]
Out[5]=
In[6]:=
%[]
Out[6]=

Find a counterexample to a more sophisticated hypothesis in group theory:

In[7]:=
counterexample = ResourceFunction["FindEquationalCounterexample"][ ForAll[{a, b, c}, inv[inv[a]] == g[inv[b], inv[c]]], {ForAll[{a, b, c}, g[a, g[b, c]] == g[g[a, b], c]], ForAll[a, g[a, e] == a], ForAll[a, g[a, inv[a]] == e]}]
Out[7]=

Show the counterexample association:

In[8]:=
counterexample["CounterexampleAssociation"]
Out[8]=

Generate a function to verify that this is a valid counterexample to the hypothesis:

In[9]:=
counterexample["FalsificationFunction"]
Out[9]=
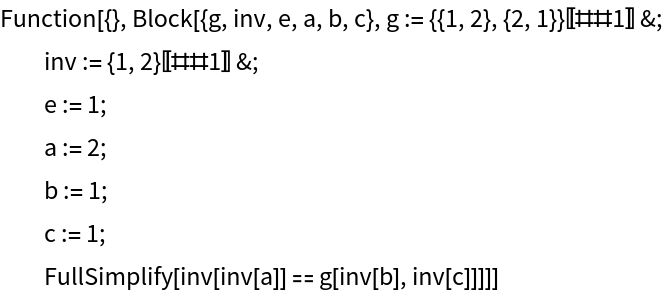
In[10]:=
%[]
Out[10]=

Generate a function to verify that this counterexample is consistent with the underlying axioms:

In[11]:=
counterexample["VerificationFunction"]
Out[11]=
In[12]:=
%[]
Out[12]=

Scope (5) 

Axiom Systems (3) 

FindEquationalCounterexample supports hypotheses formulated in any equational axiom system, including Wolfram's shortest possible axiom for Boolean algebra (finding a counterexample to the hypothesis that the Nand operator is associative):

In[13]:=
counterexample = ResourceFunction["FindEquationalCounterexample"][ ForAll[{a, b, c}, nand[nand[a, b], c] == nand[a, nand[b, c]]], ForAll[{a, b, c}, nand[nand[nand[a, b], c], nand[a, nand[nand[a, c], a]]] == c]]
Out[13]=

Show the counterexample association:

In[14]:=
counterexample["CounterexampleAssociation"]
Out[14]=

Generate a function to verify that this is a valid counterexample to the hypothesis:

In[15]:=
counterexample["FalsificationFunction"]
Out[15]=
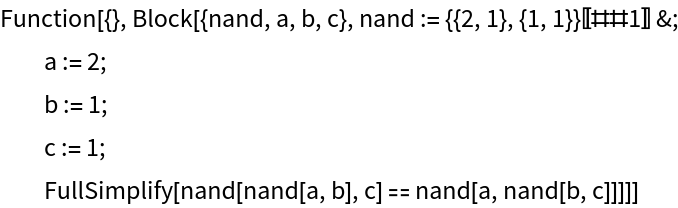
In[16]:=
%[]
Out[16]=

Generate a function to verify that this counterexample is consistent with the underlying axioms:

In[17]:=
counterexample["VerificationFunction"]
Out[17]=
In[18]:=
%[]
Out[18]=

Ring theory (finding a counterexample to the hypothesis that every ring is commutative):

In[19]:=
counterexample = ResourceFunction["FindEquationalCounterexample"][ ForAll[{a, b}, f[a, b] == f[b, a]], {ForAll[{a, b, c}, g[a, g[b, c]] == g[g[a, b], c]], ForAll[a, g[a, e] == a], ForAll[a, g[a, inv[a]] == e], ForAll[{a, b}, g[a, b] == g[b, a]], ForAll[{a, b, c}, f[a, f[b, c]] == f[f[a, b], c]], ForAll[{a, b, c}, f[a, g[b, c]] == g[f[a, b], f[a, c]]]}]
Out[19]=

Show the counterexample association:

In[20]:=
counterexample["CounterexampleAssociation"]
Out[20]=

Generate a function to verify that this is a valid counterexample to the hypothesis:

In[21]:=
counterexample["FalsificationFunction"]
Out[21]=
In[22]:=
%[]
Out[22]=

Generate a function to verify that this counterexample is consistent with the underlying axioms:

In[23]:=
counterexample["VerificationFunction"]
Out[23]=
In[24]:=
%[]
Out[24]=

Equational Presburger arithmetic (finding a counterexample to the hypothesis that every integer is equal to its negation):

In[25]:=
counterexample = ResourceFunction["FindEquationalCounterexample"][ ForAll[x, neg[x] == x], {ForAll[x, plus[x, zero] == x], ForAll[x, plus[x, neg[x]] == zero], ForAll[{x, y, z}, plus[plus[x, y], z] == plus[x, plus[y, z]]]}]
Out[25]=

Show the counterexample association:

In[26]:=
counterexample["CounterexampleAssociation"]
Out[26]=

Generate a function to verify that this is a valid counterexample to the hypothesis:

In[27]:=
counterexample["FalsificationFunction"]
Out[27]=
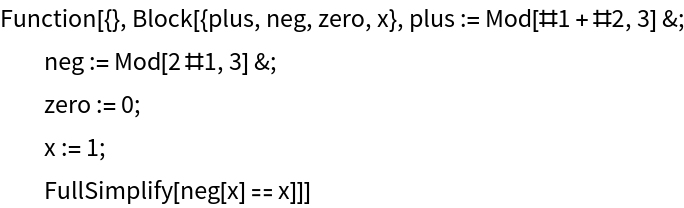
In[28]:=
%[]
Out[28]=

Generate a function to verify that this counterexample is consistent with the underlying axioms:

In[29]:=
counterexample["VerificationFunction"]
Out[29]=
In[30]:=
%[]
Out[30]=

Hypothesis and Axiom Specification (2) 

Find a counterexample from a list of axioms:

In[31]:=
ResourceFunction["FindEquationalCounterexample"][ ForAll[a, g[a, e] == e], {ForAll[{a, b, c}, g[a, g[b, c]] == g[g[a, b], c]], ForAll[a, g[a, e] == a], ForAll[a, g[a, inv[a]] == e]}]
Out[31]=

Express the axioms as a conjunction:

In[32]:=
ResourceFunction["FindEquationalCounterexample"][ ForAll[a, g[a, e] == e], ForAll[{a, b, c}, g[a, g[b, c]] == g[g[a, b], c]] && ForAll[a, g[a, e] == a] && ForAll[a, g[a, inv[a]] == e]]
Out[32]=

Find a counterexample to a list of hypotheses:

In[33]:=
counterexample = ResourceFunction[ "FindEquationalCounterexample"][{ForAll[a, g[a, e] == e], ForAll[{b, c, d}, inv[inv[b]] == g[inv[c], inv[d]]]}, {ForAll[{a, b, c}, g[a, g[b, c]] == g[g[a, b], c]], ForAll[a, g[a, e] == a], ForAll[a, g[a, inv[a]] == e]}]
Out[33]=
In[34]:=
counterexample["CounterexampleAssociation"]
Out[34]=

Express the hypotheses as a conjunction:

In[35]:=
ResourceFunction["FindEquationalCounterexample"][ ForAll[a, g[a, e] == e] && ForAll[{b, c, d}, inv[inv[b]] == g[inv[c], inv[d]]], {ForAll[{a, b, c}, g[a, g[b, c]] == g[g[a, b], c]], ForAll[a, g[a, e] == a], ForAll[a, g[a, inv[a]] == e]}]
Out[35]=

Publisher

Jonathan Gorard

Version History

  • 1.0.0 – 28 August 2020

Source Metadata

  • Citation:
    • Stephen Wolfram (2002), A New Kind of Science
    • Stephen Wolfram (2020), "A Class of Models with Potential to Represent Fundamental Physics"
    • Jonathan Gorard (2020), "Some Relativistic and Gravitational Properties of the Wolfram Model"
    • Jonathan Gorard (2020), "Some Quantum Mechanical Properties of the Wolfram Model"

Related Resources

License Information