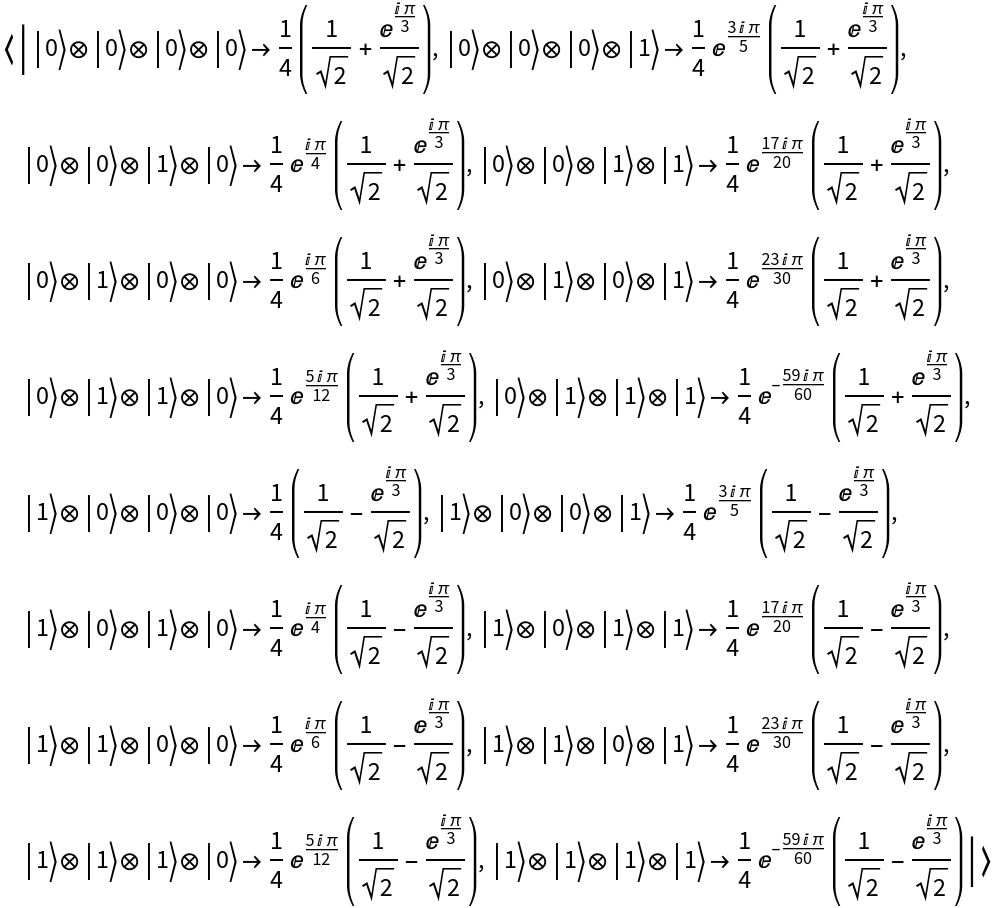Details
If ResourceFunction["ZXDiagramToQuantumDiscreteState"] succeeds in converting the specified ZXDiagramObject into a pure discrete quantum state, it will return a QuantumDiscreteState object.
ResourceFunction["ZXDiagramToQuantumDiscreteState"] works by converting each Z-spider generator in the specified
ZXDiagramObject into a qubit of the general form
{1,ⅇⅈα}, and each X-spider generator in the specified ZXDiagramObject into a qubit of the general form
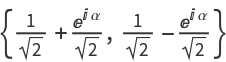
, before taking a tensor product of all such qubits to yield the desired
QuantumDiscreteState.
Since it is representing a (pure) QuantumDiscreteState, every generator/spider within the specified ZXDiagramObject should have an input arity of 0 and an output arity of 1.
In the resulting QuantumDiscreteState, the following properties are supported:
| "Amplitudes" | association <|b1→amp1,b2→amp2,…|> of basis names and amplitudes |
| "Basis" | which QuantumBasis the state is defined with respect to |
| "Picture" | which quantum mechanical picture the state is defined with respect to |
| "BasisElements" | list of basis elements bi |
| "StateVector" | state vector {amp1,amp2,…} (for pure states only) |
| "DensityMatrix" | density matrix mat (for both pure and mxied states) |
| "VonNeumannEntropy" | Von Neumann entropy (entanglement entropy) of the state |
| "Purity" | purity of the quantum state, specified as a real number |
| "PureStateQ" | whether the state is pure (purity equals 1) |
| "MixedStateQ" | whether the state is mixed (purity is not equal to 1) |
| "Qudits" | number of qudits (subsystems) within the state |
| "Dimensions" | dimensionality of each qudit (subsystem) |
| "BlochSphericalCoordinates" | spherical coordinates of the state on the Bloch sphere (qubits only) |
| "BlochCartesianCoordinates" | Cartesian coordinates of the state on the Bloch sphere (qubits only) |
| "Properties" | list of all property names |
The default convention is to name Z-spiders as z1,z2,…; X-spiders as x1,x2,…; black diamonds as d1,d2,…; outputs as o1,o2,…; etc.


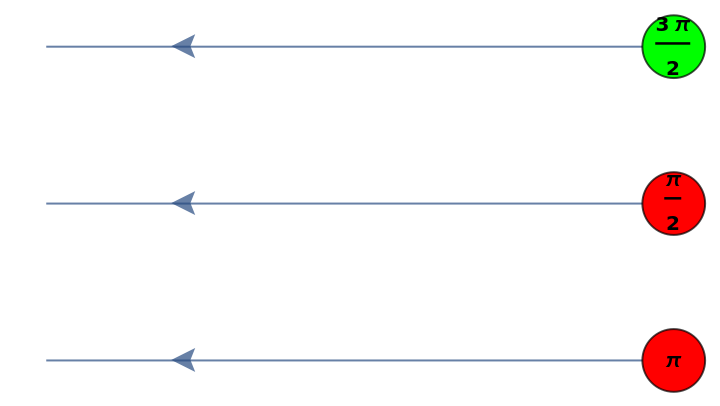
![diagram = ResourceFunction[
"MakeZXDiagram"][{\[FormalCapitalX][x1, 0, 1, Pi/2], \[FormalCapitalX][x2, 0, 1, Pi], \[FormalCapitalZ][z, 0, 1, 3 Pi/2], \[FormalCapitalW][x1, o1], \[FormalCapitalW][x2, o2], \[FormalCapitalW][z, o3]}];
diagram["LabeledGraph"]](https://www.wolframcloud.com/obj/resourcesystem/images/ea9/ea991016-f8c6-4873-985a-d83bcc8f15b7/1e88fc9075063e72.png)
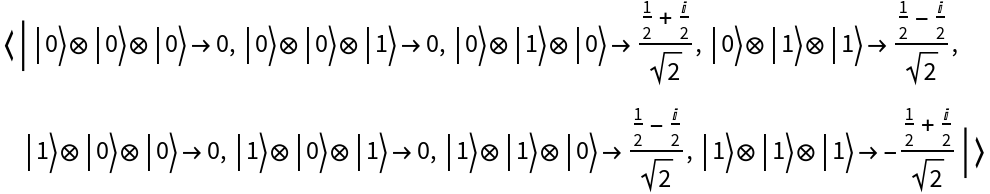
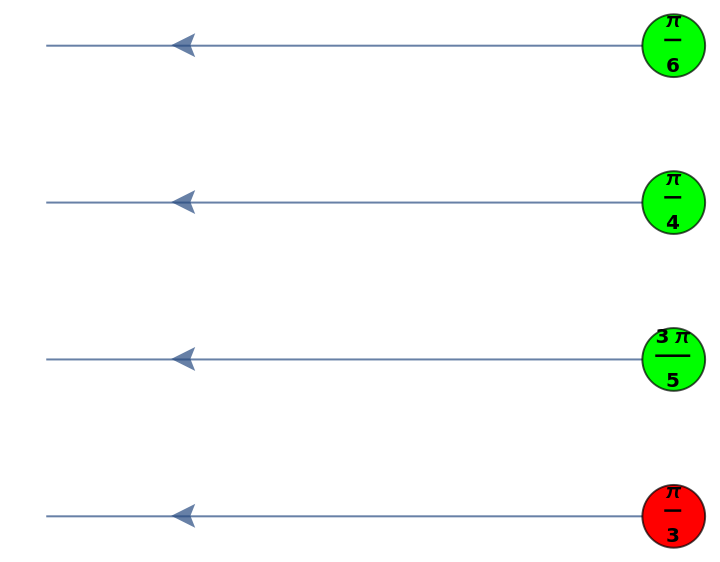
![diagram2 = ResourceFunction[
"MakeZXDiagram"][{\[FormalCapitalZ][z1, 0, 1, Pi/6], \[FormalCapitalZ][z2, 0, 1, Pi/4], \[FormalCapitalZ][z3, 0, 1, 3 Pi/5], \[FormalCapitalX][x, 0, 1, Pi/3], \[FormalCapitalW][z1, o1], \[FormalCapitalW][z2, o2], \[FormalCapitalW][z3, o3], \[FormalCapitalW][x, o4]}];
diagram2["LabeledGraph"]](https://www.wolframcloud.com/obj/resourcesystem/images/ea9/ea991016-f8c6-4873-985a-d83bcc8f15b7/62105946fd2a8538.png)