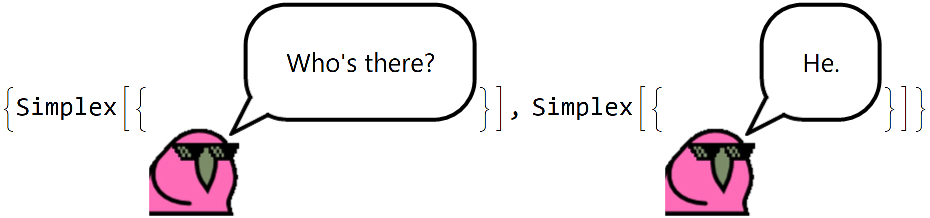Basic Examples (3)
Get the Betti numbers of a simplex:
Get the Betti numbers of a simplicial complex:
Get the Betti numbers of a MeshRegion:
Scope (4)
Many graphics primitives that represent simplices can be used:
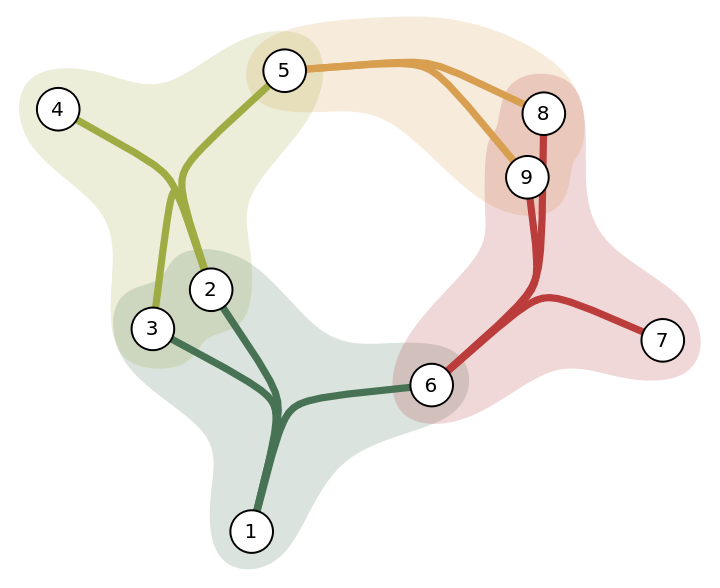
Give a simplicial complex as lists of indices:
Use the resource function HypergraphPlot to view the corresponding hypergraph to see that these correspond to three connected components, one "hole" and no "voids":
BettiNumbers can operate on graphs:
The vertices of the simplices need not be geometric coordinates:
Equivalently, as a Graph:
Applications (3)
Determine if a cow is (topologically) spherical:
This is not a spherical cow:
Determine if meshes are solid or hollow:
Verify with SimplexBoundary:
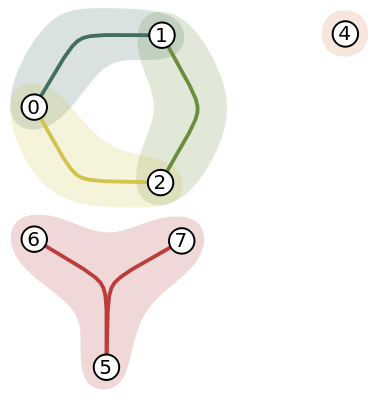
Form simplicial complexes from graphs by mapping cycles of a given length to simplices:
Check that the Betti numbers accurately characterize the underlying surfaces:
Visualize a connected embedding for each surface:
Properties and Relations (3)
Only dim+1 Betti numbers are returned, where dim is the dimension of the given simplicial complex:
The dimension of the simplicial complex is determined by the maximum dimension of simplices in the complex:
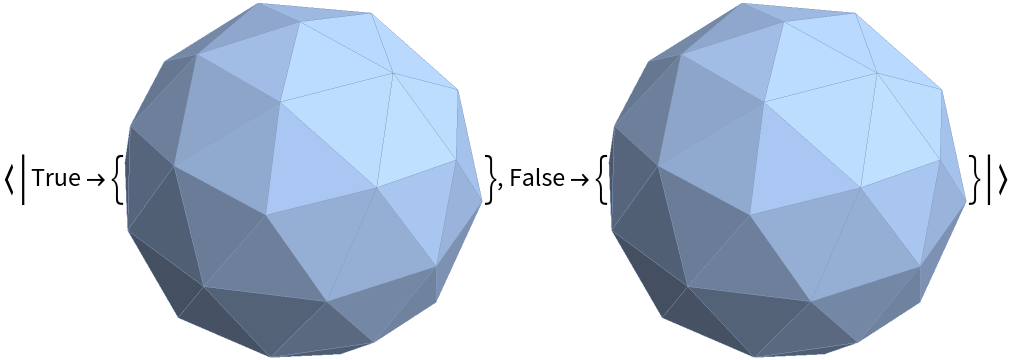
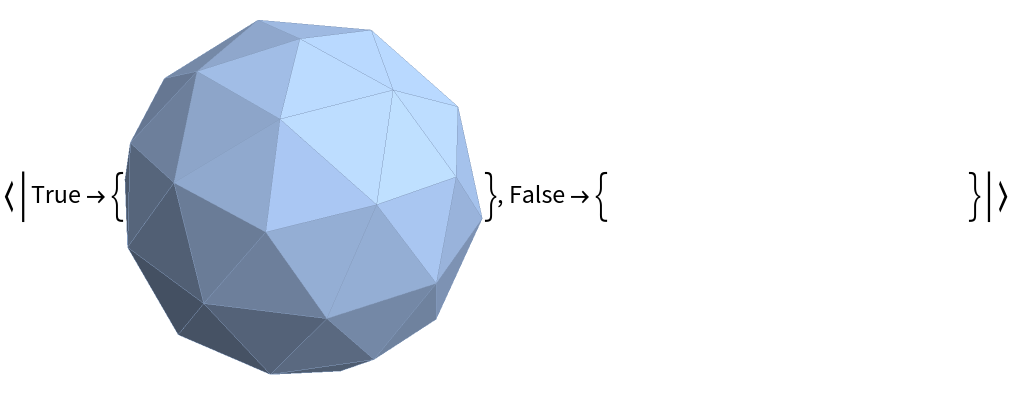
All Betti numbers after the returned values are zero, so a simplex has the same Betti numbers regardless of its dimension:
These are all equivalent:
Homology groups (3)
The homology groups of the torus T are:
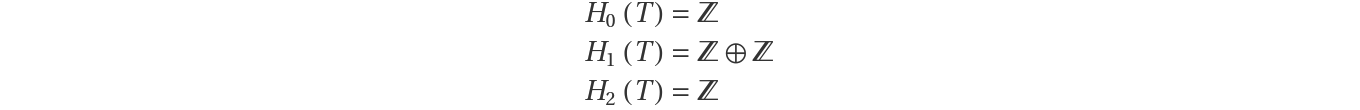
These can be obtained from Betti numbers:
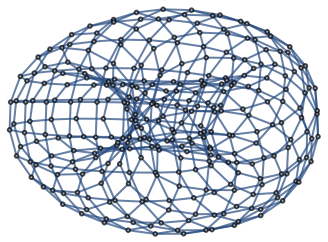
Hypergraphs (2)
The first Betti number of a connected hypergraph is 1:
The second Betti number suggests that there's a "hole" in the covering; visualize it with the resource function HypergraphPlot:
Boundaries (2)
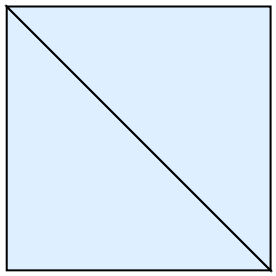
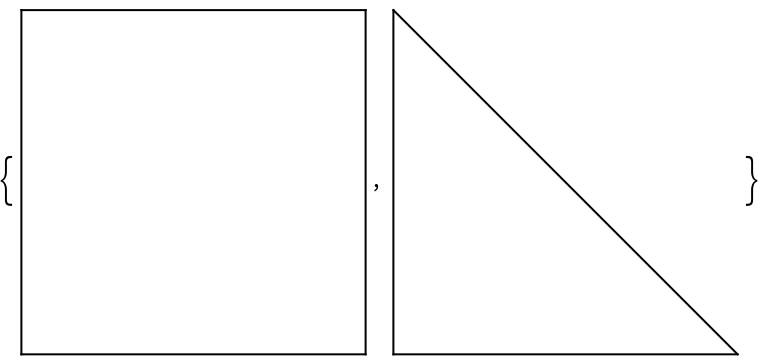
Two triangles that share an edge are topologically equivalent to one triangle:
Their boundaries should be equivalent as well:
Possible Issues (5)
BettiNumbers only considers unique vertices in each simplex:
As graphs, these are considered distinct:
The same is true for hypergraphs:
All graphs are treated as undirected:
This means that the first Betti number corresponds to the number of WeaklyConnectedGraphComponents instead of ConnectedGraphComponents:
Betti numbers do not identify links, knots or braids:
Betti numbers cannot determine orientability:
BettiNumbers only allows Polygon objects with three vertices:
Neat Examples (3)
Find some topologically interesting cities:
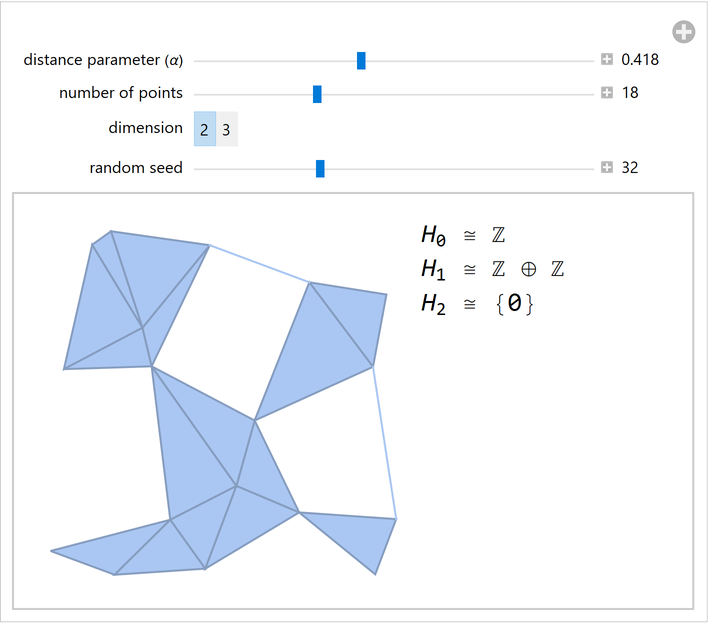
Dynamically compute homology of an alpha complex for a random set of points:
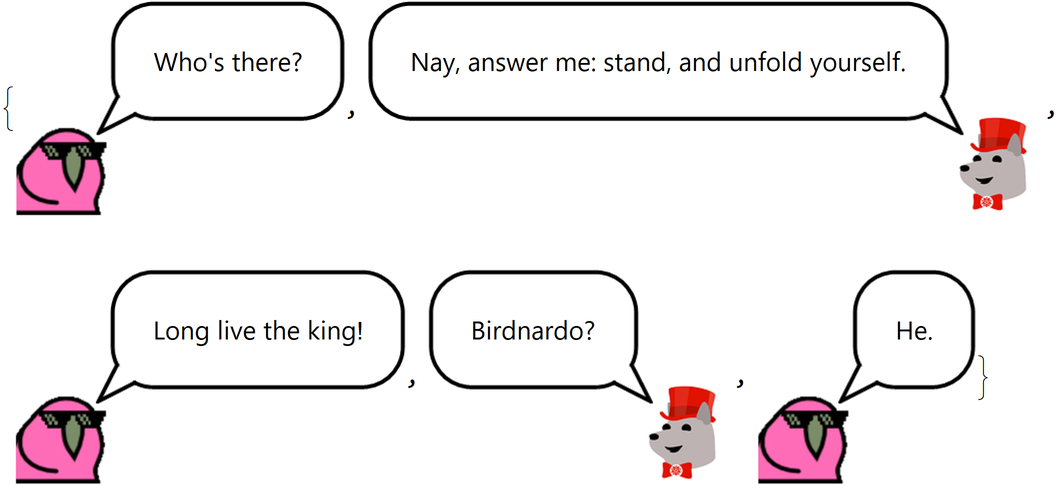
Create a simplicial complex corresponding to dialog exchanged between two actors:
This is topologically equivalent to Birdnardo talking to himself:
Find the boundary to skip to the important stuff:
![ResourceFunction["BettiNumbers"][\!\(\*
GraphicsBox[
TagBox[
DynamicModuleBox[{Typeset`mesh = {MeshRegion, {}}},
TagBox[GraphicsComplexBox[CompressedData["
1:eJxdVM9rU0EQfjaRqgmIIGJTECy0UVBE8CTY2b9A1FPBU4OC6EHQNiqR1h8n
D0oh2PYSBC+ioFQQMbQyK6gHI15qy7MIBpFarYWkohRp1Pfcbx7uhBc2k8n3
Y77d7PbC6SPH24Ig6Ive8Rq9tu7uNL0rheEzh9p/8NnqnU2jpXt8MdcfffrJ
mXLu9s6HIS8NrF7NlH/xjmIhXyx85kp4LXpavLp5LPts/zLv6bgy+OjCH3aU
K1gDm1o88b33RSvpn4/h+TYr+Fv3p2pzX9J2Efydsexouy1Bf3Km4+740fX2
bbxUmnzw2/Po2WA/xPDKAo8PnNz26UHGXh6ZHHrc9w66WQv9QPqXXJ8EX3d4
qoJ/2vGT0iflj875/knNR2p+0/LzoW4/P1qLfIWfkL/oRxxd/+2P9En6wJPg
uxw/CT/0Sfkj8Qf/SR/7YwSP+Y3wIx8j+sjPzCI/5GtmkC/yN9gf6GaN7M8Y
+iXsn8Kz4ucc9OV8ij85n4O+f07787Ga36p8uNvPj1W+rPIHX134gmOxfPEj
ufMZ8qsD1yfeTy/g9/Psvm6Cf0n5acD/76R/I0Kvq63BvPPc889fCvmEwKeT
PPN+nwQPfexvwq/OQ4OUP6r5/knmq4Mf88PHyFS/67PoY34WPPhZ6bPoY/6k
D/9W8O7+SVlfP5383zG/lfwVHvdPwq/uqwYrf/wa/iV/NR/vO5yZ4/IbftK8
OXFqdpk3oq66mvYO9XyNasqFL5/G9S7UW1zNfwH58ZfD
"],
{Hue[0.6, 0.3, 0.95], EdgeForm[Hue[0.6, 0.3, 0.75]],
TagBox[PolygonBox[{{79, 11, 10}, {80, 9, 8}, {79, 10, 9}, {7, 80, 8}, {13, 12, 78}, {78, 12, 11}, {78, 11, 79}, {9, 80, 79}, {77, 13, 78}, {7, 81, 80}, {81, 6, 5}, {82, 4, 3}, {
28, 27, 87}, {82, 5, 4}, {85, 3, 2}, {81, 5, 82}, {3, 85, 82}, {69, 84, 53}, {84, 83, 85}, {53, 70, 69}, {1, 88, 85}, {2, 1, 85}, {6, 81, 7}, {15, 14, 77}, {15, 76, 16}, {
77, 76, 15}, {14, 13, 77}, {17, 76, 75}, {16, 76, 17}, {75,
18, 17}, {75, 19, 18}, {74, 20, 19}, {19, 75, 74}, {74, 73, 21}, {26, 86, 27}, {71, 86, 72}, {73, 72, 23}, {73, 23,
22}, {22, 21, 73}, {24, 23, 72}, {25, 24, 72}, {25, 86, 26}, {25, 72, 86}, {70, 68, 86}, {74, 21, 20}, {84, 85, 54}, {51, 56, 88}, {70, 86, 71}, {56, 50, 49}, {51, 50, 56}, {49, 48, 57}, {53, 84, 54}, {55, 88, 56}, {57, 56, 49}, {54, 85, 88}, {48, 47, 57}, {68, 70, 53}, {58, 47, 46}, {59, 45, 44}, {45, 58, 46}, {43, 59, 44}, {58, 45, 59}, {59, 43, 60}, {60, 41, 61}, {41, 60, 42}, {61, 41, 40}, {42, 60, 43}, {47, 58, 57}, {68, 67, 87}, {68, 87, 86}, {87, 66, 29}, {87, 27, 86}, {31, 66, 65}, {87, 67, 66}, {87, 29, 28}, {66, 30, 29}, {66, 31, 30}, {32, 31, 65}, {54, 88, 55}, {65, 33, 32}, {85, 83, 82}, {37, 63, 62}, {51, 88, 52}, {62, 39, 38}, {62, 61, 39}, {37, 62, 38}, {33, 64, 34}, {64, 33, 65}, {34, 64, 35}, {63, 35, 64}, {63, 36, 35}, {63, 37, 36}, {40, 39, 61}, {52, 88, 1}}],
Annotation[#, "Geometry"]& ]}],
MouseAppearanceTag["LinkHand"]],
AllowKernelInitialization->False],
"MeshGraphics",
AutoDelete->True,
Editable->False,
Selectable->False],
DefaultBaseStyle->{"MeshGraphics", FrontEnd`GraphicsHighlightColor -> Hue[0.1, 1, 0.7]}]\)]](https://www.wolframcloud.com/obj/resourcesystem/images/e8a/e8aa931b-1c16-46da-a12c-fcf3680c98eb/7f88ba3506eb3052.png)
![ResourceFunction["BettiNumbers"][\!\(\*
Graphics3DBox[
TagBox[
DynamicModuleBox[{Typeset`mesh = {MeshRegion, {}}},
TagBox[GraphicsComplex3DBox[CompressedData["
1:eJyFmG9olWUYxo9OndP+rOPZzmnMLb8kDSxISxrD94EGQRt92KxOQbTKalCY
iKBk1hJxEiiM0AZFSfVhoUVkfqgkU4kWZrDICkXo7wjLD9ZsYVMKzvm9L+/v
3Wgwxntz736u+7nv63qe+1ny8FM9j87O5XKj//3W5PipD5W/1wW+V188fuKj
84Uw0PZ63eDK1pD2qw+7L6//c21Ha+jet6vv5/vy4fA/5VPdBwvhm/aD5R1b
WmJ72n9x2PtC/9EfTiwKG555ra+hWAjbLwxsfGlPc2zH/4lZO68YOtYU2xds
zq/e1rsotN/5R+OBjqYZ/EvCkw9n53x8y9G7Sxk8lb+l+Lvt0i/jZzblQ2gY
23bs5WImX+L3v/XjqpXdCzPxsRv/J2dv3NyxZn4GP3bvD3bvz/T+rcKT7D/2
m95u3zr0+LXVejbH/7/8ju9nvzpRquJqjvdn5/nhr/Z9VqzGS/b5tvzhde/0
Nlbtpdj+4qGN4dD1DVW8xTjO8D2Lj4weKFT3tTFe1/7gdHzyNR7sxk8c8iRv
1sWP/0v3SVO8DnmBA1zpvi3GeRCHPMmbde2frlcSn7yMJ90/CX7iwE/4yrr0
AX0BTvqJ/iIv+pI+xU5/0+/EgSfwhnXtD07HJy/jwW78aX4lOmU+8A1OeIWd
vODn9PZSJo71wrrANzgdn7yMJ21vzcShvuWF/Wt2NM/L1Hfr/Lu6Hts9L1Pf
Yu2RVSfHajP1PVd3+t7Jcl2mvpU4CzL13T93xc2dVyW6Zn/Xl/iuL3hcX/Cb
v51dDZMfPHQxMn9X/PTsxOCyqcj8HW/+8v6RdbkMf3edfr7ljXJNhr+nttc/
N/je3Ax/x3o+3bJ2ONln+5u/xDd/wWP+gt/63Lds79CS9b/G+cLz95c++eCZ
R85F1uc517yy54u2C5H1uWK/FFmfK/s/K6PPlfrWZPQZf+sz8a3P4LE+gz9d
30Kof/fD4y1Xfx7nC89HevZveHrpd3G+6MLXvX/f3tn1W+T7QNO3t765/MrJ
KF33fCj/XnvD5MjlKF3ffBg4+cBfm0ZzIb1u4g9Ox/e5DJ503RP8vg/kUj+J
flTqPhr5flLh+3jke05l/yZmsE9l4lQXzOgW/sZJfN83wGM7+ImDTrm+8Nz1
RRdcX3TE9UV3XF90yvW1Pzgdn7yMB7vxEwedMn/hufmLLpi/6Ij5i+6Yv+iU
+Wt/cDo+eRkPduMnDnlan/GzPhPX+gwO6zO4rc/kaX22Pzgdn7yMB7vxE4c+
9vlLH/j8pW98/tJnPn/pS5+/9LHPX/uD0/HJy3iwG39aB2bWKb7BiS5gJy90
ZHr7VCbO/+kU3+lzJIlPXsaD3fhdX9+f2R/fn9lP35/Zf9+fqZfvz9TX92f7
u76+PxuP6+v7M/z1fET/ez6CL56P4JfnI/jo+Qj+ej6yv/nr+ch4zF/PR+iU
51947vkXXfD8i454/kV3PP+iU55/7W999vxrPNZnz7/olN9t4LnfZ9AFv8Og
I35vQXf8roJO+f3E/j5//R5iPD5//b7xL0+XFdQ=
"],
{Hue[0.6, 0.3, 0.85], EdgeForm[Hue[0.6, 0.3, 0.75]],
TagBox[Polygon3DBox[CompressedData["
1:eJwBwQQ++yFib1JiAgAAAJABAAADAAAAAQIDAwIEAwQFBQQGBQYHBwYIBwgJ
CQgKCQoLCwoMCwwNDQwODQ4PDw4QDxARERASERITExIUExQBARQCAhUEBBUW
BBYGBhYXBhcICBcYCBgKChgZChkMDBkaDBoODhobDhsQEBscEBwSEhwdEh0U
FB0eFB4CAh4VFR8WFh8gFiAXFyAhFyEYGCEiGCIZGSIjGSMaGiMkGiQbGyQl
GyUcHCUmHCYdHSYnHSceHicoHigVFSgfHykgICkqICohISorISsiIissIiwj
IywtIy0kJC0uJC4lJS4vJS8mJi8wJjAnJzAxJzEoKDEyKDIfHzIpKTMqKjM0
KjQrKzQ1KzUsLDU2LDYtLTY3LTcuLjc4LjgvLzg5LzkwMDk6MDoxMTo7MTsy
Mjs8MjwpKTwzMz00ND0+ND41NT4/NT82Nj9ANkA3N0BBN0E4OEFCOEI5OUJD
OUM6OkNEOkQ7O0RFO0U8PEVGPEYzM0Y9PUc+PkdIPkg/P0hJP0lAQElKQEpB
QUpLQUtCQktMQkxDQ0xNQ01ERE1ORE5FRU5PRU9GRk9QRlA9PVBHR1FISFFS
SFJJSVJTSVNKSlNUSlRLS1RVS1VMTFVWTFZNTVZXTVdOTldYTlhPT1hZT1lQ
UFlaUFpHR1pRUVtSUltcUlxTU1xdU11UVF1eVF5VVV5fVV9WVl9gVmBXV2Bh
V2FYWGFiWGJZWWJjWWNaWmNkWmRRUWRbW2VcXGVmXGZdXWZnXWdeXmdoXmhf
X2hpX2lgYGlqYGphYWprYWtiYmtsYmxjY2xtY21kZG1uZG5bW25lZW9mZm9w
ZnBnZ3BxZ3FoaHFyaHJpaXJzaXNqanN0anRra3R1a3VsbHV2bHZtbXZ3bXdu
bnd4bnhlZXhvb3lwcHl6cHpxcXp7cXtycnt8cnxzc3x9c310dH1+dH51dX5/
dX92dn+AdoB3d4CBd4F4eIGCeIJvb4J5eYN6eoOEeoR7e4SFe4V8fIWGfIZ9
fYaHfYd+foeIfoh/f4iJf4mAgImKgIqBgYqLgYuCgouMgox5eYyDg42EhI2O
hI6FhY6PhY+Gho+QhpCHh5CRh5GIiJGSiJKJiZKTiZOKipOUipSLi5SVi5WM
jJWWjJaDg5aNjZeOjpeYjpiPj5iZj5mQkJmakJqRkZqbkZuSkpuckpyTk5yd
k52UlJ2elJ6VlZ6flZ+Wlp+glqCNjaCXl6GYmKGimKKZmaKjmaOamqOkmqSb
m6Slm6WcnKWmnKadnaannaeenqeonqifn6ipn6mgoKmqoKqXl6qhoauioqus
oqyjo6yto62kpK2upK6lpa6vpa+mpq+wprCnp7Cxp7GoqLGyqLKpqbKzqbOq
qrO0qrShobSrq7WsrLW2rLatrba3rbeurre4rrivr7i5r7mwsLm6sLqxsbq7
sbuysru8sryzs7y9s720tL2+tL6rq761tb+2tr/AtsC3t8DBt8G4uMHCuMK5
ucLDucO6usPEusS7u8TFu8W8vMXGvMa9vcbHvce+vsfIvsi1tci/vwHAwAED
wAPBwQMFwQXCwgUHwgfDwwcJwwnExAkLxAvFxQsNxQ3Gxg0Pxg/Hxw8RxxHI
yBETyBO/vxMBxinZZA==
"]],
Annotation[#, "Geometry"]& ]}],
MouseAppearanceTag["LinkHand"]],
AllowKernelInitialization->False],
"MeshGraphics3D",
AutoDelete->True,
Editable->False,
Selectable->False],
Boxed->False,
DefaultBaseStyle->{"MeshGraphics3D", FrontEnd`GraphicsHighlightColor -> Hue[0.1, 1, 0.7]},
Lighting->{{"Ambient",
GrayLevel[0.45]}, {"Directional",
GrayLevel[0.3],
ImageScaled[{2, 0, 2}]}, {"Directional",
GrayLevel[0.33],
ImageScaled[{2, 2, 2}]}, {"Directional",
GrayLevel[0.3],
ImageScaled[{0, 2, 2}]}},
Method->{"ShrinkWrap" -> True},
ViewPoint->{1.3, -2.4, 2.},
ViewVertical->{0., 0., 1.}]\)]](https://www.wolframcloud.com/obj/resourcesystem/images/e8a/e8aa931b-1c16-46da-a12c-fcf3680c98eb/44e066c7ffc43bb0.png)
![ResourceFunction["BettiNumbers"][\!\(\*
GraphicsBox[
NamespaceBox["NetworkGraphics",
DynamicModuleBox[{Typeset`graph = HoldComplete[
Graph[{1, 2, 3, 4, 5, 6, 7, 8, 9, 10}, {Null,
SparseArray[
Automatic, {10, 10}, 0, {1, {{0, 1, 4, 5, 7, 9, 9, 11, 14, 15, 16}, {{8}, {4}, {
5}, {7}, {8}, {2}, {5}, {2}, {4}, {2}, {9}, {1}, {3}, {
10}, {7}, {8}}}, Pattern}]}]]},
TagBox[GraphicsGroupBox[
GraphicsComplexBox[{{
1.1766424360997711`, -0.2971773146947261}, {
1.2002458694720275`, -2.778126641410253}, {
0.2971773146947262, -1.791095294316216}, {
0.29717731469472586`, -2.3992205633172983`}, {
0.2973266153984717, -3.1573057652742027`}, {
0.2971773146947261, -3.751660394663655}, {
2.405344817398942, -2.7781665828345727`}, {
1.1662103033309261`, -1.2977375562233502`}, {
3.432428408274397, -2.77825463644212}, {
2.0281679525984555`, -1.8048659339278466`}}, {
{Hue[0.6, 0.7, 0.5], Opacity[0.7], LineBox[{{1, 8}, {2, 4}, {2, 5}, {2, 7}, {3, 8}, {4, 5}, {
7, 9}, {8, 10}}]},
{Hue[0.6, 0.2, 0.8], EdgeForm[{GrayLevel[0], Opacity[0.7]}], DiskBox[1, 0.03341240067237147], DiskBox[2, 0.03341240067237147], DiskBox[3, 0.03341240067237147], DiskBox[4, 0.03341240067237147], DiskBox[5, 0.03341240067237147], DiskBox[6, 0.03341240067237147], DiskBox[7, 0.03341240067237147], DiskBox[8, 0.03341240067237147], DiskBox[9, 0.03341240067237147], DiskBox[10, 0.03341240067237147]}}]],
MouseAppearanceTag["NetworkGraphics"]],
AllowKernelInitialization->False]],
DefaultBaseStyle->{"NetworkGraphics", FrontEnd`GraphicsHighlightColor -> Hue[0.8, 1., 0.6]},
FormatType->TraditionalForm,
FrameTicks->None,
ImageSize->{75., Automatic}]\)]](https://www.wolframcloud.com/obj/resourcesystem/images/e8a/e8aa931b-1c16-46da-a12c-fcf3680c98eb/5163cf6c71e28ad2.png)
![(* Evaluate this cell to get the example input *) CloudGet["https://www.wolframcloud.com/obj/89cca2ce-1a1f-4d29-ba35-9eeab0e8a569"]](https://www.wolframcloud.com/obj/resourcesystem/images/e8a/e8aa931b-1c16-46da-a12c-fcf3680c98eb/08ba1a71108e8e58.png)

![meshes = {\!\(\*
Graphics3DBox[
TagBox[
DynamicModuleBox[{
Typeset`mesh = {MeshRegion, {Boxed -> False, Lighting -> {{"Ambient",
GrayLevel[0.45]}, {"Directional",
GrayLevel[0.3],
ImageScaled[{2, 0, 2}]}, {"Directional",
GrayLevel[0.33],
ImageScaled[{2, 2, 2}]}, {"Directional",
GrayLevel[0.3],
ImageScaled[{0, 2, 2}]}}}}},
TagBox[GraphicsComplex3DBox[CompressedData["
1:eJxTTMoPSmViYGDQBmJmIE6IKmVRPv9o/7Iv02eXP35pz4AVfICLi3MqyOZu
uLj/CbMbd4fFa/vbb/cfVZ1/Zz+aejgfzfz9OMzZDzMHqt4e3T1Q9fZo9tr/
D3ER5st/t9/3pb75+2OX4eph5sL4PMELeU9demBf8Tu/8KT68/3cUP5NqDlo
9sL1Va4u5lnJ+sz+938QuL+fF6oPzT0w99s/A/Nvw9wDDyc0e/ffRFVvD3M/
zDx+sLoL9suh4cAP1Qc1x54H1f37oe7cD3WnPdSdMPfuRw+XTYmev6tPH9n/
B6r+KVR8peunjcW1sTbo8YlmPtxcNHP2w8xBCzeYe9DjC+4uNP/uh/kXLXzg
6QUWrmjxux9qvj26+WjicH2Q8HuDxr9jD/WXPZq/oPFwYT+aO+H+QwtndHNg
4YyeTuDpGs18WLxD4/nNfjR3oqcHWLqCxmPuHuz5eAE0fhfsgdEAZNfRvQ==
"],
{Hue[0.6, 0.3, 0.85], EdgeForm[Hue[0.6, 0.3, 0.75]],
TagBox[TetrahedronBox[CompressedData["
1:eJwNzcdxhEAAAMFjWbxZvPceJhmVQrgElP9PPPo3VTN//36/4vP5/Lzk68oc
prmh7GO6u8e/O/q6Iy5K3NYhzy5U5NJYE+M0EPghRV5S5xXj7VPlF/09cCiX
fohxMo3hHvFlSDykjH5AkeUYVYvTXrTVheO5aJ5DMI+M80SwzcxbwzClTFZK
WfeUeU0nferKJFwCpGlgVgZJEZPEKamVYFsNtrB41MGyBaxqYY0URrTSRgZu
1OJ6B9ve0JmSrjaRa0i4LhirxBIJelaw2w2aLtAyne3ZeY6d5dlY1MPhnZye
xn6cCP3ti/d7CvbTRpwa//VzI5c=
"]],
Annotation[#, "Geometry"]& ]}],
MouseAppearanceTag["LinkHand"]],
AllowKernelInitialization->False],
"MeshGraphics3D",
AutoDelete->True,
Editable->False,
Selectable->False],
Boxed->False,
DefaultBaseStyle->{"MeshGraphics3D", FrontEnd`GraphicsHighlightColor -> Hue[0.1, 1, 0.7]},
Lighting->{{"Ambient",
GrayLevel[0.45]}, {"Directional",
GrayLevel[0.3],
ImageScaled[{2, 0, 2}]}, {"Directional",
GrayLevel[0.33],
ImageScaled[{2, 2, 2}]}, {"Directional",
GrayLevel[0.3],
ImageScaled[{0, 2, 2}]}},
Method->{"ShrinkWrap" -> True}]\), \!\(\*
Graphics3DBox[
TagBox[
DynamicModuleBox[{
Typeset`mesh = {MeshRegion, {Boxed -> False, Lighting -> {{"Ambient",
GrayLevel[0.45]}, {"Directional",
GrayLevel[0.3],
ImageScaled[{2, 0, 2}]}, {"Directional",
GrayLevel[0.33],
ImageScaled[{2, 2, 2}]}, {"Directional",
GrayLevel[0.3],
ImageScaled[{0, 2, 2}]}}}}},
TagBox[GraphicsComplex3DBox[CompressedData["
1:eJx1kc0rhFEUxm+GhWbGLCysFEnKxpKFejYoCxuslEJZTm+ahGTvP7CwkA1N
NlirsxkKC18rjSIfo8nXJLtXjTHvPbfmae6tW+/767nPec45nXPB+HyDMaa3
cmOVmx3+PsisTQ+amlOSiKePiOP2Q467t95FSfR/J5aDOJbDYOG05xWJie3k
2fWDqJ44iEu8Vg/iqkdbc0d7ev9KnmMj8fWBN8lbH+IgDtKDuOrB/evXzNRi
Y9fFo+z8bGwuPRUdT1XzXcqu5Smbl/Ri6p6SeHyEfOCpC6rr5qI6nXd5cqi1
JfiUsWJf/9fJjfMh7t6t7GUS2aYCwvL/uZdk/TxCPmCfQjVP3vnrvImDOIjL
4exouHqek98oD14stznF5oTNqXldDo+PeHzce5qD+oP69e1F9yjUl9uT9k37
0pygnK4+9QXS63zwB+Ylzig=
"],
{Hue[0.6, 0.3, 0.85], EdgeForm[Hue[0.6, 0.3, 0.75]],
TagBox[Polygon3DBox[{{14, 13, 10}, {17, 16, 9}, {19, 13, 12}, {22, 21,
8}, {25, 24, 11}, {27, 21, 7}, {29, 20, 6}, {31, 14, 10}, {32, 30, 1}, {34, 33, 9}, {35, 19, 12}, {23, 16, 7}, {37, 17, 9}, {38, 33, 1}, {39, 29, 6}, {26, 36, 4}, {
40, 18, 11}, {41, 24, 4}, {42, 35, 12}, {28, 15, 8}, {15,
14, 8}, {13, 15, 12}, {15, 13, 14}, {18, 17, 11}, {16, 18, 7}, {18, 16, 17}, {20, 19, 6}, {13, 20, 10}, {20, 13,
19}, {23, 22, 3}, {21, 23, 7}, {23, 21, 22}, {26, 25, 5}, {24, 26, 4}, {26, 24, 25}, {28, 27, 2}, {21, 28, 8}, {28, 21, 27}, {30, 29, 1}, {20, 30, 10}, {30, 20, 29}, {22, 31, 3}, {14, 22, 8}, {22, 14, 31}, {31, 32, 3}, {30, 31, 10}, {31, 30, 32}, {32, 34, 3}, {33, 32, 1}, {32, 33, 34}, {36, 35, 4}, {19, 36, 6}, {36, 19, 35}, {34, 23, 3}, {16, 34, 9}, {34, 16, 23}, {25, 37, 5}, {17, 25, 11}, {25, 17, 37}, {37, 38, 5}, {33, 37, 9}, {37, 33, 38}, {38, 39, 5}, {29, 38, 1}, {38, 29, 39}, {39, 26, 5}, {36, 39, 6}, {39, 36, 26}, {27, 40, 2}, {18, 27, 7}, {27, 18, 40}, {40, 41, 2}, {24, 40, 11}, {40, 24, 41}, {41, 42, 2}, {35, 41, 4}, {41, 35, 42}, {42, 28, 2}, {15, 42, 12}, {42, 15, 28}}],
Annotation[#, "Geometry"]& ]}],
MouseAppearanceTag["LinkHand"]],
AllowKernelInitialization->False],
"MeshGraphics3D",
AutoDelete->True,
Editable->False,
Selectable->False],
Boxed->False,
DefaultBaseStyle->{"MeshGraphics3D", FrontEnd`GraphicsHighlightColor -> Hue[0.1, 1, 0.7]},
Lighting->{{"Ambient",
GrayLevel[0.45]}, {"Directional",
GrayLevel[0.3],
ImageScaled[{2, 0, 2}]}, {"Directional",
GrayLevel[0.33],
ImageScaled[{2, 2, 2}]}, {"Directional",
GrayLevel[0.3],
ImageScaled[{0, 2, 2}]}},
Method->{"ShrinkWrap" -> True}]\)};](https://www.wolframcloud.com/obj/resourcesystem/images/e8a/e8aa931b-1c16-46da-a12c-fcf3680c98eb/144105893ec616eb.png)

![Graphics3D[{EdgeForm[None], FaceForm[Opacity[.25]], ts /. Dispatch[
Thread[VertexList[t] -> GraphEmbedding[t, "SpringElectricalEmbedding", 3]]]}, Boxed -> False]](https://www.wolframcloud.com/obj/resourcesystem/images/e8a/e8aa931b-1c16-46da-a12c-fcf3680c98eb/5c4c9870a75231f9.png)

![Graphics3D[{EdgeForm[None], FaceForm[Opacity[.25]], ks /. Dispatch[
Thread[VertexList[k] -> GraphEmbedding[k, "SpringElectricalEmbedding", 3]]]}, Boxed -> False]](https://www.wolframcloud.com/obj/resourcesystem/images/e8a/e8aa931b-1c16-46da-a12c-fcf3680c98eb/0b58cc523221f382.png)


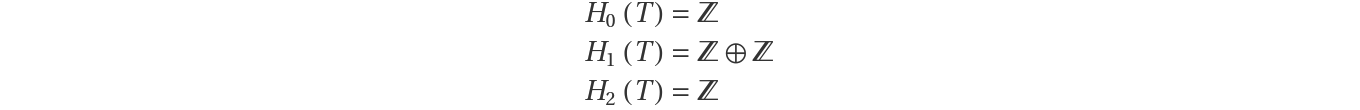
![showHomology[s_] := TraditionalForm[
Grid[MapIndexed[{Subscript[H, First[#2] - 1], "=", Replace[#1, {0 -> {0}, 1 -> \[DoubleStruckCapitalZ], n_ :> CirclePlus @@ ConstantArray[\[DoubleStruckCapitalZ], n]}]} &, ResourceFunction["BettiNumbers"][s]], Alignment -> Left]];](https://www.wolframcloud.com/obj/resourcesystem/images/e8a/e8aa931b-1c16-46da-a12c-fcf3680c98eb/3325f3d4bedfb8db.png)
![showHomology[\!\(\*
Graphics3DBox[
TagBox[
DynamicModuleBox[{Typeset`mesh = {MeshRegion, {}}},
TagBox[GraphicsComplex3DBox[CompressedData["
1:eJyFmG9olWUYxo9OndP+rOPZzmnMLb8kDSxISxrD94EGQRt92KxOQbTKalCY
iKBk1hJxEiiM0AZFSfVhoUVkfqgkU4kWZrDICkXo7wjLD9ZsYVMKzvm9L+/v
3Wgwxntz736u+7nv63qe+1ny8FM9j87O5XKj//3W5PipD5W/1wW+V188fuKj
84Uw0PZ63eDK1pD2qw+7L6//c21Ha+jet6vv5/vy4fA/5VPdBwvhm/aD5R1b
WmJ72n9x2PtC/9EfTiwKG555ra+hWAjbLwxsfGlPc2zH/4lZO68YOtYU2xds
zq/e1rsotN/5R+OBjqYZ/EvCkw9n53x8y9G7Sxk8lb+l+Lvt0i/jZzblQ2gY
23bs5WImX+L3v/XjqpXdCzPxsRv/J2dv3NyxZn4GP3bvD3bvz/T+rcKT7D/2
m95u3zr0+LXVejbH/7/8ju9nvzpRquJqjvdn5/nhr/Z9VqzGS/b5tvzhde/0
Nlbtpdj+4qGN4dD1DVW8xTjO8D2Lj4weKFT3tTFe1/7gdHzyNR7sxk8c8iRv
1sWP/0v3SVO8DnmBA1zpvi3GeRCHPMmbde2frlcSn7yMJ90/CX7iwE/4yrr0
AX0BTvqJ/iIv+pI+xU5/0+/EgSfwhnXtD07HJy/jwW78aX4lOmU+8A1OeIWd
vODn9PZSJo71wrrANzgdn7yMJ21vzcShvuWF/Wt2NM/L1Hfr/Lu6Hts9L1Pf
Yu2RVSfHajP1PVd3+t7Jcl2mvpU4CzL13T93xc2dVyW6Zn/Xl/iuL3hcX/Cb
v51dDZMfPHQxMn9X/PTsxOCyqcj8HW/+8v6RdbkMf3edfr7ljXJNhr+nttc/
N/je3Ax/x3o+3bJ2ONln+5u/xDd/wWP+gt/63Lds79CS9b/G+cLz95c++eCZ
R85F1uc517yy54u2C5H1uWK/FFmfK/s/K6PPlfrWZPQZf+sz8a3P4LE+gz9d
30Kof/fD4y1Xfx7nC89HevZveHrpd3G+6MLXvX/f3tn1W+T7QNO3t765/MrJ
KF33fCj/XnvD5MjlKF3ffBg4+cBfm0ZzIb1u4g9Ox/e5DJ503RP8vg/kUj+J
flTqPhr5flLh+3jke05l/yZmsE9l4lQXzOgW/sZJfN83wGM7+ImDTrm+8Nz1
RRdcX3TE9UV3XF90yvW1Pzgdn7yMB7vxEwedMn/hufmLLpi/6Ij5i+6Yv+iU
+Wt/cDo+eRkPduMnDnlan/GzPhPX+gwO6zO4rc/kaX22Pzgdn7yMB7vxE4c+
9vlLH/j8pW98/tJnPn/pS5+/9LHPX/uD0/HJy3iwG39aB2bWKb7BiS5gJy90
ZHr7VCbO/+kU3+lzJIlPXsaD3fhdX9+f2R/fn9lP35/Zf9+fqZfvz9TX92f7
u76+PxuP6+v7M/z1fET/ez6CL56P4JfnI/jo+Qj+ej6yv/nr+ch4zF/PR+iU
51947vkXXfD8i454/kV3PP+iU55/7W999vxrPNZnz7/olN9t4LnfZ9AFv8Og
I35vQXf8roJO+f3E/j5//R5iPD5//b7xL0+XFdQ=
"],
{Hue[0.6, 0.3, 0.85], EdgeForm[Hue[0.6, 0.3, 0.75]],
TagBox[Polygon3DBox[CompressedData["
1:eJwBwQQ++yFib1JiAgAAAJABAAADAAAAAQIDAwIEAwQFBQQGBQYHBwYIBwgJ
CQgKCQoLCwoMCwwNDQwODQ4PDw4QDxARERASERITExIUExQBARQCAhUEBBUW
BBYGBhYXBhcICBcYCBgKChgZChkMDBkaDBoODhobDhsQEBscEBwSEhwdEh0U
FB0eFB4CAh4VFR8WFh8gFiAXFyAhFyEYGCEiGCIZGSIjGSMaGiMkGiQbGyQl
GyUcHCUmHCYdHSYnHSceHicoHigVFSgfHykgICkqICohISorISsiIissIiwj
IywtIy0kJC0uJC4lJS4vJS8mJi8wJjAnJzAxJzEoKDEyKDIfHzIpKTMqKjM0
KjQrKzQ1KzUsLDU2LDYtLTY3LTcuLjc4LjgvLzg5LzkwMDk6MDoxMTo7MTsy
Mjs8MjwpKTwzMz00ND0+ND41NT4/NT82Nj9ANkA3N0BBN0E4OEFCOEI5OUJD
OUM6OkNEOkQ7O0RFO0U8PEVGPEYzM0Y9PUc+PkdIPkg/P0hJP0lAQElKQEpB
QUpLQUtCQktMQkxDQ0xNQ01ERE1ORE5FRU5PRU9GRk9QRlA9PVBHR1FISFFS
SFJJSVJTSVNKSlNUSlRLS1RVS1VMTFVWTFZNTVZXTVdOTldYTlhPT1hZT1lQ
UFlaUFpHR1pRUVtSUltcUlxTU1xdU11UVF1eVF5VVV5fVV9WVl9gVmBXV2Bh
V2FYWGFiWGJZWWJjWWNaWmNkWmRRUWRbW2VcXGVmXGZdXWZnXWdeXmdoXmhf
X2hpX2lgYGlqYGphYWprYWtiYmtsYmxjY2xtY21kZG1uZG5bW25lZW9mZm9w
ZnBnZ3BxZ3FoaHFyaHJpaXJzaXNqanN0anRra3R1a3VsbHV2bHZtbXZ3bXdu
bnd4bnhlZXhvb3lwcHl6cHpxcXp7cXtycnt8cnxzc3x9c310dH1+dH51dX5/
dX92dn+AdoB3d4CBd4F4eIGCeIJvb4J5eYN6eoOEeoR7e4SFe4V8fIWGfIZ9
fYaHfYd+foeIfoh/f4iJf4mAgImKgIqBgYqLgYuCgouMgox5eYyDg42EhI2O
hI6FhY6PhY+Gho+QhpCHh5CRh5GIiJGSiJKJiZKTiZOKipOUipSLi5SVi5WM
jJWWjJaDg5aNjZeOjpeYjpiPj5iZj5mQkJmakJqRkZqbkZuSkpuckpyTk5yd
k52UlJ2elJ6VlZ6flZ+Wlp+glqCNjaCXl6GYmKGimKKZmaKjmaOamqOkmqSb
m6Slm6WcnKWmnKadnaannaeenqeonqifn6ipn6mgoKmqoKqXl6qhoauioqus
oqyjo6yto62kpK2upK6lpa6vpa+mpq+wprCnp7Cxp7GoqLGyqLKpqbKzqbOq
qrO0qrShobSrq7WsrLW2rLatrba3rbeurre4rrivr7i5r7mwsLm6sLqxsbq7
sbuysru8sryzs7y9s720tL2+tL6rq761tb+2tr/AtsC3t8DBt8G4uMHCuMK5
ucLDucO6usPEusS7u8TFu8W8vMXGvMa9vcbHvce+vsfIvsi1tci/vwHAwAED
wAPBwQMFwQXCwgUHwgfDwwcJwwnExAkLxAvFxQsNxQ3Gxg0Pxg/Hxw8RxxHI
yBETyBO/vxMBxinZZA==
"]],
Annotation[#, "Geometry"]& ]}],
MouseAppearanceTag["LinkHand"]],
AllowKernelInitialization->False],
"MeshGraphics3D",
AutoDelete->True,
Editable->False,
Selectable->False],
Boxed->False,
DefaultBaseStyle->{"MeshGraphics3D", FrontEnd`GraphicsHighlightColor -> Hue[0.1, 1, 0.7]},
ImageSize->{90., 62.419354838709694`},
Lighting->{{"Ambient",
GrayLevel[0.45]}, {"Directional",
GrayLevel[0.3],
ImageScaled[{2, 0, 2}]}, {"Directional",
GrayLevel[0.33],
ImageScaled[{2, 2, 2}]}, {"Directional",
GrayLevel[0.3],
ImageScaled[{0, 2, 2}]}},
Method->{"ShrinkWrap" -> True},
ViewPoint->{1.3, -2.4, 2.},
ViewVertical->{0., 0., 1.}]\)]](https://www.wolframcloud.com/obj/resourcesystem/images/e8a/e8aa931b-1c16-46da-a12c-fcf3680c98eb/2e28cf6f1cf06168.png)
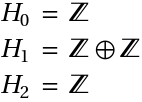
![ResourceFunction["BettiNumbers"][\!\(\*
GraphicsBox[
NamespaceBox["NetworkGraphics",
DynamicModuleBox[{Typeset`graph = HoldComplete[
Graph[{1, 2, 3, 4, 5}, {{{1, 2}, {2, 3}, {3, 1}, {3, 4}, {4, 5}, {3, 5}}, Null}, {EdgeStyle -> {
Arrowheads[Small]}, VertexSize -> {Medium}}]], Typeset`boxes, Typeset`boxes$s2d =
GraphicsGroupBox[{{
Arrowheads[0.03374070617041407],
Directive[
Opacity[0.7],
Hue[0.6, 0.7, 0.5]],
StyleBox[
ArrowBox[
LineBox[{
DynamicLocation["VertexID$1", Automatic, Center],
DynamicLocation["VertexID$2", Automatic, Center]}]],
Arrowheads[Small], StripOnInput -> False],
StyleBox[
ArrowBox[
LineBox[{
DynamicLocation["VertexID$2", Automatic, Center],
DynamicLocation["VertexID$3", Automatic, Center]}]],
Arrowheads[Small], StripOnInput -> False],
StyleBox[
ArrowBox[
LineBox[{
DynamicLocation["VertexID$3", Automatic, Center],
DynamicLocation["VertexID$1", Automatic, Center]}]],
Arrowheads[Small], StripOnInput -> False],
StyleBox[
ArrowBox[
LineBox[{
DynamicLocation["VertexID$3", Automatic, Center],
DynamicLocation["VertexID$4", Automatic, Center]}]],
Arrowheads[Small], StripOnInput -> False],
StyleBox[
ArrowBox[
LineBox[{
DynamicLocation["VertexID$3", Automatic, Center],
DynamicLocation["VertexID$5", Automatic, Center]}]],
Arrowheads[Small], StripOnInput -> False],
StyleBox[
ArrowBox[
LineBox[{
DynamicLocation["VertexID$4", Automatic, Center],
DynamicLocation["VertexID$5", Automatic, Center]}]],
Arrowheads[Small], StripOnInput -> False]}, {
Directive[
Hue[0.6, 0.2, 0.8],
EdgeForm[
Directive[
GrayLevel[0],
Opacity[0.7]]]],
TagBox[
DiskBox[{2.017540427513767, 0.000442083090181955}, 0.08017300398243705], "DynamicName", BoxID -> "VertexID$1"],
TagBox[
DiskBox[{2.017313637850549, 0.8021720908379496}, 0.08017300398243705],
"DynamicName", BoxID -> "VertexID$2"],
TagBox[
DiskBox[{1.0081041532060644`, 0.4011713309635613}, 0.08017300398243705], "DynamicName", BoxID -> "VertexID$3"],
TagBox[
DiskBox[{0., 0.}, 0.08017300398243705], "DynamicName", BoxID -> "VertexID$4"],
TagBox[
DiskBox[{0.00022442849777104534`, 0.8026134053739986}, 0.08017300398243705], "DynamicName", BoxID -> "VertexID$5"]}}], $CellContext`flag},
TagBox[
DynamicBox[GraphComputation`NetworkGraphicsBox[
3, Typeset`graph, Typeset`boxes, $CellContext`flag], {CachedValue :> Typeset`boxes, SingleEvaluation -> True, SynchronousUpdating -> False, TrackedSymbols :> {$CellContext`flag}},
ImageSizeCache->{{0.9900000000000007, 98.51000000000002}, {-24.144871762947535`, 20.0896}}],
MouseAppearanceTag["NetworkGraphics"]],
AllowKernelInitialization->False,
UnsavedVariables:>{$CellContext`flag}]],
DefaultBaseStyle->{"NetworkGraphics", FrontEnd`GraphicsHighlightColor -> Hue[0.8, 1., 0.6]},
FrameTicks->None,
ImageSize->{99.5, Automatic}]\)]](https://www.wolframcloud.com/obj/resourcesystem/images/e8a/e8aa931b-1c16-46da-a12c-fcf3680c98eb/04d8041626ee91ab.png)
![ResourceFunction["BettiNumbers"][\!\(\*
GraphicsBox[
NamespaceBox["NetworkGraphics",
DynamicModuleBox[{Typeset`graph = HoldComplete[
Graph[{1, 2, 3, 4, 5}, {Null,
SparseArray[
Automatic, {5, 5}, 0, {1, {{0, 2, 4, 8, 10, 12}, {{3}, {2}, {1}, {3}, {2}, {
1}, {4}, {5}, {3}, {5}, {3}, {4}}}, Pattern}]}, {EdgeStyle -> {
Arrowheads[Small]}, ImageSize -> {99.5, Automatic}, VertexSize -> {Medium}}]]},
TagBox[GraphicsGroupBox[
GraphicsComplexBox[{{2.017540427513767, 0.000442083090181955}, {2.017313637850549, 0.8021720908379496}, {1.0081041532060644`, 0.4011713309635613}, {0., 0.}, {0.00022442849777104534`, 0.8026134053739986}}, {
{Hue[0.6, 0.7, 0.5], Opacity[0.7], Arrowheads[Small], LineBox[{{1, 3}, {1, 2}, {2, 3}, {3, 4}, {3, 5}, {4, 5}}]},
{Hue[0.6, 0.2, 0.8], EdgeForm[{GrayLevel[0], Opacity[0.7]}], DiskBox[1, 0.08017300398243705], DiskBox[2, 0.08017300398243705], DiskBox[3, 0.08017300398243705], DiskBox[4, 0.08017300398243705], DiskBox[5, 0.08017300398243705]}}]],
MouseAppearanceTag["NetworkGraphics"]],
AllowKernelInitialization->False]],
DefaultBaseStyle->{"NetworkGraphics", FrontEnd`GraphicsHighlightColor -> Hue[0.8, 1., 0.6]},
FormatType->TraditionalForm,
FrameTicks->None,
ImageSize->{99.5, Automatic}]\)]](https://www.wolframcloud.com/obj/resourcesystem/images/e8a/e8aa931b-1c16-46da-a12c-fcf3680c98eb/744f6bda510b323e.png)
![Length[ConnectedGraphComponents[\!\(\*
GraphicsBox[
NamespaceBox["NetworkGraphics",
DynamicModuleBox[{Typeset`graph = HoldComplete[
Graph[{1, 2, 3, 4, 5}, {{{1, 2}, {2, 3}, {3, 1}, {3, 4}, {4, 5}, {3, 5}}, Null}, {EdgeStyle -> {
Arrowheads[Small]}, VertexSize -> {Medium}}]], Typeset`boxes, Typeset`boxes$s2d = GraphicsGroupBox[{{
Arrowheads[0.03374070617041407],
Directive[
Opacity[0.7],
Hue[0.6, 0.7, 0.5]],
StyleBox[
ArrowBox[
LineBox[{
DynamicLocation["VertexID$1", Automatic, Center],
DynamicLocation["VertexID$2", Automatic, Center]}]],
Arrowheads[Small], StripOnInput -> False],
StyleBox[
ArrowBox[
LineBox[{
DynamicLocation["VertexID$2", Automatic, Center],
DynamicLocation["VertexID$3", Automatic, Center]}]],
Arrowheads[Small], StripOnInput -> False],
StyleBox[
ArrowBox[
LineBox[{
DynamicLocation["VertexID$3", Automatic, Center],
DynamicLocation["VertexID$1", Automatic, Center]}]],
Arrowheads[Small], StripOnInput -> False],
StyleBox[
ArrowBox[
LineBox[{
DynamicLocation["VertexID$3", Automatic, Center],
DynamicLocation["VertexID$4", Automatic, Center]}]],
Arrowheads[Small], StripOnInput -> False],
StyleBox[
ArrowBox[
LineBox[{
DynamicLocation["VertexID$3", Automatic, Center],
DynamicLocation["VertexID$5", Automatic, Center]}]],
Arrowheads[Small], StripOnInput -> False],
StyleBox[
ArrowBox[
LineBox[{
DynamicLocation["VertexID$4", Automatic, Center],
DynamicLocation["VertexID$5", Automatic, Center]}]],
Arrowheads[Small], StripOnInput -> False]}, {
Directive[
Hue[0.6, 0.2, 0.8],
EdgeForm[
Directive[
GrayLevel[0],
Opacity[0.7]]]],
TagBox[
DiskBox[{2.017540427513767, 0.000442083090181955}, 0.08017300398243705], "DynamicName", BoxID -> "VertexID$1"],
TagBox[
DiskBox[{2.017313637850549, 0.8021720908379496}, 0.08017300398243705],
"DynamicName", BoxID -> "VertexID$2"],
TagBox[
DiskBox[{1.0081041532060644`, 0.4011713309635613}, 0.08017300398243705], "DynamicName", BoxID -> "VertexID$3"],
TagBox[
DiskBox[{0., 0.}, 0.08017300398243705], "DynamicName", BoxID -> "VertexID$4"],
TagBox[
DiskBox[{0.00022442849777104534`, 0.8026134053739986}, 0.08017300398243705], "DynamicName", BoxID -> "VertexID$5"]}}], $CellContext`flag},
TagBox[
DynamicBox[GraphComputation`NetworkGraphicsBox[
3, Typeset`graph, Typeset`boxes, $CellContext`flag], {CachedValue :> Typeset`boxes, SingleEvaluation -> True, SynchronousUpdating -> False, TrackedSymbols :> {$CellContext`flag}},
ImageSizeCache->{{0.9900000000000007, 98.51000000000002}, {-24.144871762947535`, 20.0896}}],
MouseAppearanceTag["NetworkGraphics"]],
AllowKernelInitialization->False,
UnsavedVariables:>{$CellContext`flag}]],
DefaultBaseStyle->{"NetworkGraphics", FrontEnd`GraphicsHighlightColor -> Hue[0.8, 1., 0.6]},
FrameTicks->None,
ImageSize->{99.5, Automatic}]\)]]](https://www.wolframcloud.com/obj/resourcesystem/images/e8a/e8aa931b-1c16-46da-a12c-fcf3680c98eb/7f17d6c0960a9300.png)
![Length[WeaklyConnectedGraphComponents[\!\(\*
GraphicsBox[
NamespaceBox["NetworkGraphics",
DynamicModuleBox[{Typeset`graph = HoldComplete[
Graph[{1, 2, 3, 4, 5}, {{{1, 2}, {2, 3}, {3, 1}, {3, 4}, {4, 5}, {3, 5}}, Null}, {EdgeStyle -> {
Arrowheads[Small]}, VertexSize -> {Medium}}]], Typeset`boxes, Typeset`boxes$s2d = GraphicsGroupBox[{{
Arrowheads[0.03374070617041407],
Directive[
Opacity[0.7],
Hue[0.6, 0.7, 0.5]],
StyleBox[
ArrowBox[
LineBox[{
DynamicLocation["VertexID$1", Automatic, Center],
DynamicLocation["VertexID$2", Automatic, Center]}]],
Arrowheads[Small], StripOnInput -> False],
StyleBox[
ArrowBox[
LineBox[{
DynamicLocation["VertexID$2", Automatic, Center],
DynamicLocation["VertexID$3", Automatic, Center]}]],
Arrowheads[Small], StripOnInput -> False],
StyleBox[
ArrowBox[
LineBox[{
DynamicLocation["VertexID$3", Automatic, Center],
DynamicLocation["VertexID$1", Automatic, Center]}]],
Arrowheads[Small], StripOnInput -> False],
StyleBox[
ArrowBox[
LineBox[{
DynamicLocation["VertexID$3", Automatic, Center],
DynamicLocation["VertexID$4", Automatic, Center]}]],
Arrowheads[Small], StripOnInput -> False],
StyleBox[
ArrowBox[
LineBox[{
DynamicLocation["VertexID$3", Automatic, Center],
DynamicLocation["VertexID$5", Automatic, Center]}]],
Arrowheads[Small], StripOnInput -> False],
StyleBox[
ArrowBox[
LineBox[{
DynamicLocation["VertexID$4", Automatic, Center],
DynamicLocation["VertexID$5", Automatic, Center]}]],
Arrowheads[Small], StripOnInput -> False]}, {
Directive[
Hue[0.6, 0.2, 0.8],
EdgeForm[
Directive[
GrayLevel[0],
Opacity[0.7]]]],
TagBox[
DiskBox[{2.017540427513767, 0.000442083090181955}, 0.08017300398243705], "DynamicName", BoxID -> "VertexID$1"],
TagBox[
DiskBox[{2.017313637850549, 0.8021720908379496}, 0.08017300398243705],
"DynamicName", BoxID -> "VertexID$2"],
TagBox[
DiskBox[{1.0081041532060644`, 0.4011713309635613}, 0.08017300398243705], "DynamicName", BoxID -> "VertexID$3"],
TagBox[
DiskBox[{0., 0.}, 0.08017300398243705], "DynamicName", BoxID -> "VertexID$4"],
TagBox[
DiskBox[{0.00022442849777104534`, 0.8026134053739986}, 0.08017300398243705], "DynamicName", BoxID -> "VertexID$5"]}}], $CellContext`flag},
TagBox[
DynamicBox[GraphComputation`NetworkGraphicsBox[
3, Typeset`graph, Typeset`boxes, $CellContext`flag], {CachedValue :> Typeset`boxes, SingleEvaluation -> True, SynchronousUpdating -> False, TrackedSymbols :> {$CellContext`flag}},
ImageSizeCache->{{0.9900000000000007, 98.51000000000002}, {-24.144871762947535`, 20.0896}}],
MouseAppearanceTag["NetworkGraphics"]],
AllowKernelInitialization->False,
UnsavedVariables:>{$CellContext`flag}]],
DefaultBaseStyle->{"NetworkGraphics", FrontEnd`GraphicsHighlightColor -> Hue[0.8, 1., 0.6]},
FrameTicks->None,
ImageSize->{99.5, Automatic}]\)]]](https://www.wolframcloud.com/obj/resourcesystem/images/e8a/e8aa931b-1c16-46da-a12c-fcf3680c98eb/648de3427e179801.png)
![ResourceFunction["BettiNumbers"][\!\(\*
Graphics3DBox[
TagBox[
DynamicModuleBox[{Typeset`mesh = {MeshRegion, {}}},
TagBox[GraphicsComplex3DBox[CompressedData["
1:eJx1mntwltURxoNGgggYDIEkkISQkCuEehtQge+VInRsnFrAVvCWUqzp0AGh
A4iIWqhIKYK0eAMHqAKKINiKCmj7Lko1MnIVrKAWQUQbMUTugkKdnHc38/1e
Tv7QYbPZffbst7vPnvMVDB896M7zUlJSbv7hP+en6M+PghT8jD7V98WhByuD
zZ/u/Wr6pRfZ769/YO3Engt62L9vHzYutXDLvsS8KbVDhs2uDJ797HTq8jUt
A5U7/UrTPzukf0ab0fWJw3dU7t87v3vQ5vPpbXvfd2Gg8lcfHDCt9lfdY/o3
tPzi5UOjugVX7xt1MvtYGvS7xfAs+aLqxxMmVQRLGvE0NzxOq0lff7aM/qBu
Ql5FcO+BzLxNieb2e4/90GM/9OAPPfhDz/mEnvMJPecfes4/vOKek1cPf68i
uPbWguKtH2fb381a0/H+AZMrguuOv730499m2/n872Tf9eUry4OFix4YX9c7
y865rlFeFlStX9Lu69r2Ju9/1fDUi/eUBktH3r7/1PxMs7Ng4kMDj8wuDV64
IPXOtLJM8+vRDz32Qw+e0IM/7LwyPaOmvjhwcReY3y6Tfj24fnVx4P6uwHDe
uDVxzbi84sD56WxxLf100IzxI7oG738zecpNt+ab/P0re4z9flNRMH3shhZ5
/8o1OzvPm/KPqXOLgj5HWs4+kJ9rfj36ocd+6METevBH+e0cuHotMr/69+5z
UWQ4G8//js6B+3wVWly5Y3p+N/NUfuA+p11Mvj3C5z7vTefm4swPXN00nbNH
P/TYDz14Qg/+0HlpF/krRh23C1x9dEW9q7zI4lK5q9dCj7xLzE70aYr5hX6Y
LG+Ky4MHcsMfjujbu7T+6W8TzO+6Xi2OL5t1KsH87r+y/uOH075PML9v585J
O9AyJZbfWzqlnh4ysFksv9Oy6/ZeJs1i+fXohx77oQdP6MEfpo556Mng9ydC
1m+7XR3nj33uWMj6vW/KmV3LjjSErN/qlpVLagYeCFm/1esOXLcy3BWyfhcN
C24c/+j2kPXr0Q899kMPntCDP9zaOF8vFvbnXo1zorWwPy92/V3Yn5e6OSTs
z+mN8+N8YX92c+48YX/26Ice+6EHT+jBH/736ORhL3+YKeQVV1wwZ9nqvEwh
f9gf3lr7Vs8MIU+Y127zXXs+SRfygbkLLm/9ydethXO/dzh0+Z6JrYTz3aMf
euyHHjyhB39U11mSgp/Hzow9Mqp3B5MrTifPNLnGNbLZI63mvHWJR54esxNl
M+bXox967IcePKEHP/Nrv8f5iCe/4smvePIrnvyaX48+8yue/Ionv+KpX/OL
z7946lc89Sue+hVP/Zpfjz7rVzz1K576FU9/Nr/ob+Lpz+Lpz+Lpz+Lpz+bX
o8/+LJ7+LJ7+LJ75a34xv8Qzf8Uzf8Uzf8Uzf82vR5/zVzzzVzzzV5L7lfEr
9A/jJ5LcZ4zPWFwqj/iPR94lZsf9v0vML/TJrywuDx7yK7MD/mx+wT8NJ/iq
xQV+a3LwYbMD/mx+PfrkzxaXBw/5s9nBfmR+sV8YTuwjTf0qeX8xOfYds4P9
yPx69LkfWVwePNyPkF/bf80v9kfDiX3T4sJ+anLss2YH+6/59ehz/0UeY3i4
/5od3NuYX9wPGE7cM1hcuK8wOe49zA7uT8yvR5/3IRaXBw/vN9AHCoK6Hj23
tRrUNli8fsTd+UWtAsdD8oOfdy4duK0uz+Su/jubfl6r9VlHR6YHbr7nB28U
vDJ4+Mo8kzuek2/6Y7+ad+83e9oGjifkBmOeOb2rPD3P5I5HdYrpO76RE6T9
bdSmp6pyoZ8Tw3P9lqem1R/PivB0MrmLNycW74I9K3Ye+oF/lxT2qz4yppPJ
ab/VyIGrfnF3Wsy+yol/xIq/fnXL9NQYfpXzfFTO81E5z1/98vxVXtPQMG7D
k9lB+wErJo16oqvF1amxH2YFWRlnXz96W1c7H9c/OwT9az56dtI7RXbOro9k
BvPvqT98X+smues7GUHtpo27z59QaHZcn8oINs7L7TijT6H5pb7ipH2Nl3hU
TvxqZ8qaflWL1l4clKXPfbZmXLn5nXHwkRvWvt8mmHrjaweqissNZ99rzx7c
MfGHz/uju8su/WWZxfXklJ+W7Z5zYSQvNXnVf96oPdYzLbhq2/e/y5xeYnaG
XNRiY5tBzYO5bQte+rZXifmlvuKkfY2LeFRO/Gqn19SHVxW+fTAx4i+7M6sf
625+Z846lLFiX11ids6If1b36m44e80tHNDQ8HniixPvVn3Zv5vFtbXthLe2
PL8n0e+ZKZ2Od6gweWnunpKb/70zMe+BL5dPLmo6t62Xr2qoObMtsSFt7OD7
3ykzv9RXnLSvcRGPyolf7bj6TZVjT8yvab6s0vyqPOhw074+AytR7yrvbnGp
/IWsffWbW3bzyCtidpzf8phf1SdOta9xEc+55ZVm567G+u0gzG9UF8L8PtxY
X+2F+XX8J1OYX2cnU5hfV7+ZwvxSX3HSvsZFPKhrYX4dvyoQ1q/jJwXC+nV8
pkBYv47/dBbWr+MN+cL6dTwjX1i/1FectK9xEY/Kid/6diO/Khb2Z8dPioX9
2fGZrsL+7PhPkbA/O75UKOzPjl8VCvsz9RUn7WtcxKNy4lc7jl+VCXmF4ydl
Qv7g+EypkCc4/lMi5AOOLxUL577jV8XC+U59xUn7Ghfx2HwH/uQ+UCHkG26O
l0uMtzTKy4T8x+1ppR55ScyO81sS80t9xUn7yXyjzCMvj9nR/GZ9d+nufhu/
TjC/GxreHbfuxUMJ5nfmsY0Fr//scIL5veL0mcFnbzuWYH5vP7n/6k8+OJFg
flcffqnFU7UnE8yv6jO/ap/5VTzMr+Jn/a68eceyaZnNhPX76sz85Qt7pAjr
d8ebBY+NX346ZP1Ov25d6z98dCxk/TbUP121puSbkPWbsvI3C3a8Vh+yflWf
9av2Wb+Kh/Wr+Nmf75e1i18bcImwP192bUrFg8+3FfbnL9cP+PtPWqYL+/P2
qY8Mn9OulbA/934oZ3SXD1sI+/PSac9Nenl+mrA/qz77s9pnf1Y87M+Kn/P3
6IYBf1o6LUs4f6/fOfTD597rIJy/p2Z3PfHq55nC+fvS/scf3/7nDOH8rV44
/JW9i5vOTefv6lXjUj+rSxfOX9Xn/FX7nL+Kh/NX8ZO3tN9aW3nkxRwhz1m+
+Zouw+uyhbzIyTsIedQftt10zR/HZHrkGTE7zu8lMb+qT5xqnzxK8Zxbni3k
z8yv8k/mV/kq86v8lvlVPsz8Kn9mfqlP/sz8Eg/5M/Or+xHrV/cL1q/uI6xf
3V9Yv7rvsH51P2L9Up/7EeuXeLgfsX51/2V/1v2R/Vn3TfZn3U/Zn3WfZX/W
/Zf9mfrcf9mfiYf7L/uz3ttw/ur9AOev3jNw/up9Beev3ntw/ur9Cecv9RUn
7fPeg/OX+JP7gN1fift3J55DqHLcn0jV8lnV+4fm0X6octzPyKIZNW/u3ZRP
nKHKcf9j+ogX+jkxPDg3w+PiyInFi/O3eGl/9ZAxCzsuzY7ZVznxV497ok/e
ZVkx/Crn+aic56Nynr/65fmrHPUbaFz4/Ad6PqiXhJ4z6svkqMeE2kH9JtQv
9RUn7Wu8xKNy4lc76M8WL/qbxYt+GGhc6J8mR781O+jP5pf6ipP2NS7iUTnx
qx3MX/OL+WU4Me8sLsxHk2Oemh3MX/NLfcVJ+xoX8aic+NUO+JX5BT8Jkuvd
+IzFBf7jkWfE7ET8KuZX9YlT7WtcxHNuebbZAX82v+CfhhN81eICvzU5+HCQ
XL/Gn+G3SV9x0r7GRTyoa2F+sR+ZX+wXhhP7iMWF/aVJnrzvmB3sR+aX+oqT
9jUu4lE58VvfTt5/zS/2R8OJfdP6MPZTk2Oftf6M/df6M/UVJ+1rXMSjcuJX
O7jfsDmL+wGb17hPsLmP+weT477C7OB+w/xSX3HSvsZFPDbfgT+5D9j9lahf
3P808Zbk+yLjP7hfgrwkZsf5KYn5pb7ipP1kvlHmkZfH7OB+Upjf6H5PmN/o
PlCY3+j+UJjf6L5RmN/oflKYX9VnftU+86t4mF/Fz/qN7p/NL+5vhfUb3fcK
6ze6HxbWb3SfLKzf6P7Z/FKf9av2Wb+Kh/Wr+Nmfo/cF84v7eWF/ju7zhf05
uv8X9ufovUDYn6P3BfNLffZntc/+rHjYnxU/52/0fmR+8f4inL/Re41w/kbv
O8L5G70HCedv9H4Ev036nL9qn/NX8XD+Kn7yluh90PyqPHpfE/Ki6D1OyKOi
9zuPvCJmJ3ofjPlVfeJU++RRiufc8kohf2Z+8X4q5M/ML95nhfyZ+cX7r/ml
Pvkz80s85M/ML973zS/ex4X7EesX7+/C/Yj1i/d980t97kesX+LhfsT6xfc3
zC++/yDcf9mf8f0K4f7L/ozvb5hf6nP/ZX8mHu6/7M/43pH5xfdbDCe+JxO7
b+H8xfd2muZR8vd/zC/1FSft896D85f41c7/AZHow74=
"],
{Hue[0.6, 0.3, 0.85], EdgeForm[Hue[0.6, 0.3, 0.75]], EdgeForm[None], Specularity[
GrayLevel[0.2], 30],
TagBox[Polygon3DBox[CompressedData["
1:eJxN2mfUz/Ufx/Hsvffee++9994zZIWskBWyQlYo0i6VrJAVskJ2yqi0hKyQ
FbJCf5/zfzjne+N13o/Pde9557rxPb8c3Z9vOTDmU089tSr2U0/FenxjPF54
x7Lg2BxuHAuOy+HGs+D4HG4CC07I4Say4MQcbhILTsrhJrPg5BxuCgtOyeGm
suDUnFpfDI5pafTE5rScVk9cTsfp9MTn9JxeT0LOwBn0JOaMnFFPUs7EmfQk
58ycWU9KzsJZ9KTmrJw10phVW1g2PWk5O2fXk45zcA496Tkn59STgXNxLj0Z
OTfn1pOJ83AePZk5L+fVk4XzcT49WTk/54805tcWVkBPdi7IBfXk4EJcSE9O
LsyF9eTiIlxET24uykX15OFiXExPXi7OxfXk4xJcQk9+LsklI40ltYWV0lOQ
S3NpPYW4DJfRU5jLclk9Rbgcl9NTlMtzeT3FuAJX0FOcK3JFPSW4ElfSU5Ir
c+VIY2VtYVX0lOaqXFVPGa7G1fSU5epcXU85rsE19JTnmlxTTwWuxbX0VOTa
XFtPJa7DdfRU5rpcN9JYV1tYPT1VuT7X11ONG3ADPdW5ITfUU4MbcSM9Nbkx
N9ZTi5twEz21uSk31VOHm3EzPXW5OTePNDbXFtZCT31uyS31NOBW3EpPQ27N
rfU04jbcRk9jbstt9TThdtxOT1Nuz+31NOMO3EFPc+7IHSONHbWFPa2nJXfi
TnpacWfurKc1d+EuetrwM/yMnrbclbvqacfduJue9tydu+vpwD24h56O3JN7
Rhp7agt7Vk8n7sW99HTm3txbTxfuw330PMPP8XN6unJf7qunG/fjfnq6c3/u
r6cHD+ABenryQB4YaRyoLex5Pb14EA/S05sH82A9fXgID9HzHL/AL+jpy0N5
qJ5+PIyH6enPw3m4ngE8gkfoGcgjeWSkcaS2sBf1DOJRPErPYB7No/UM4TE8
Rs8L/BK/pGcoj+WxeobxOB6nZziP5/F6RvAEnqBnJE/kiZHGidrCXtYziifx
JD2jeTJP1jOGp/AUPS/xK/yKnrE8lafqGcfTeJqe8Tydp+uZwDN4hp6JPJNn
Rhpnagt7Vc8knsWz9Ezm2TxbzxSew3P0vMKv8Wt6pvLr/LqeaTyX5+qZzvN4
np4Z/Aa/oWcmz+f5kcb52sLe1DOL3+K39Mzmt/ltPXP4HX5Hz2v8Lr+r53V+
j9/TM5ff5/f1zOMP+AM9b/CH/KGe+byAF0QaF2gL+0jPW/wxf6znbf6EP9Hz
Di/khXre5U/5Uz3v8SJepOd9XsyL9XzAS3iJng95KS/Vs4CX8bJI4zJtYZ/p
+ZiX83I9n/AKXqFnIa/klXo+5c/5cz2LeBWv0rOYV/NqPUt4Da/Rs5TX8lo9
y3gdr4s0rtMW9oWe5bye1+tZwRt4g56VvJE36vmcv+Qv9aziTbxJz2rezJv1
rOEtvEXPWt7KW/Ws4228LdK4TVvYV3rW83bermcD7+AdejbyTt6p50v+mr/W
s4l38S49m3k379azhffwHj1beS/v1bON9/G+SOM+bWEx9GznWBxLzw6Ow3H0
7OR4HE/P15yAE+jZxYk4kZ7dnIST6NnDyTiZnr2cglPo2cepOFWkMZW2/Y93
4PG+seCDHO63Fvwdh3vIgg9zuEcs+CiH+70F/8Dh/mjBxzjcnyz4Zw73Fwv+
lcP9zYKP83F9+/mA/a7nIJ/gE3q+45N8Us9hPsWn9BzlP/gPPT/waT6t5xif
4TN6fuazfFbPr3yOz+k5zuf5fKTxvLawP/Wc4At8Qc9JvsgX9ZziS3xJzx/8
F/+l5zRf5st6zvAVvqLnLF/lq3rO8TW+puc8X+frkcbr2sL+1nOBb/ANPRf5
Jt/Uc4lv8S09f/E//I+ey3ybb+u5wnf4jp6rfJfv6rnG9/ienut8n+9HGu9r
C/tXzw1+wA/03OSH/FDPLX7Ej/T8w//xf3puc/jHcdu9oyk4hne4dzUFx/QO
956m4Fje4d7XFBzbO9wnjcH/6osT4/89Dziud7gPNQXH8w73kabg+N7h/qcp
OIF3gicfvf0tISfUGIMTcSKNMTkxJ9YYi5NwEo2xOSknjTQGx7FkGuNyck6u
MR6n4BQa43NKTqknAafiVHoScmpOrScRp+E0ehJzWk6rJwmn43TaknJ6Th9p
TK8tLIOe5JyRM+pJwZk4k56UnJkz60nFWTiLntSclbPqScPZOJuetJyds+tJ
xzk4h570nJNzRhpzagvLpScj5+bcejJxHs6jJzPn5bx6snA+zqcnK+fn/Hqy
cQEuoCc7F+SCenJwIS6kJycX5sKRxsLaworoyc1FuaiePFyMi+nJy8W5uJ58
XIJL6MnPJbmkngJcikvpKcilubSeQlyGy+gpzGW5bKSxrLawcnqKcnkur6cY
V+AKeopzRa6opwRX4kp6SnJlrqynFFfhKnpKc1WuqqcMV+Nqespyda4eaayu
LayGnvJck2vqqcC1uJaeilyba+upxHW4jp7KXJfr6qnC9bienqpcn+vrqcYN
uIGe6tyQG0YaG2oLa6SnJjfmxnpqcRNuoqc2N+WmeupwM26mpy435+Z66nEL
bqGnPrfklnoacCtupacht+bWkcbW2sLa6GnMbbmtnibcjtvpacrtub2eZtyB
O+hpzh25o54W/DQ/racld+JOelpxZ+6spzV34S6Rxi7awp7R05a7clc97bgb
d9PTnrtzdz0duAf30NORe3JPPU/zs/ysnk7ci3vp6cy9ubeeLtyH+0Qa+2gL
e05PV+7LffV0437cT0937s/99fTgATxAT08eyAP1PMvP8/N6evEgHqSnNw/m
wXr68BAeEmkcoi3sBT19eSgP1dOPh/EwPf15OA/XM4BH8Ag9A3kkj9TzPL/I
L+oZxKN4lJ7BPJpH6xnCY3hMpHGMtrCX9AzlsTxWzzAex+P0DOfxPF7PCJ7A
E/SM5Ik8Uc+L/DK/rGcUT+JJekbzZJ6sZwxP4SmRxinawl7RM5an8lQ943ga
T9MznqfzdD0TeAbP0DORZ/JMPS/zq/yqnkk8i2fpmcyzebaeKTyH50Qa52gL
C987pmoK/sY73Gmagr/1Dne6puBD3uHO0BR8xDvcmZqCv/cO91VNwT96hztL
U/BP3uHO1hT8i3e4czQF/+Yd7pPG4ND22mO//nhzLXgeh/uGBc/ncN+04Lc4
3Lct+B0O910Lfo/Dfd+CP+BwP7TgBRzuRxb8MYf7iQUv5HBfs4Xawj7VM48X
8SI983kxL9bzFi/hJXre4aW8VM97vIyX6fmAP+PP9Czg5bxcz8e8glfoWcgr
eWWkcaW2sM/1LOJVvErPYl7Nq/Us4TW8Rs9SXstr9SzjdbxOz2f8BX+hZzmv
5/V6VvAG3qBnJW/kjZHGjdrCvtSzijfxJj2reTNv1rOGt/AWPWt5K2/Vs463
8TY9X/BX/JWe9bydt+vZwDt4h56NvJN3Rhp3agv7Ws8m3sW79Gzm3bxbzxbe
w3v0bOW9vFfPNt7H+/R8xft5v57tfIAP6NnB3/A3enbyQT4YaTyoLexbPbv4
O/5Oz24+xIf07OHDfFjPXj7CR/Ts46N8VM9+/p6/13OAf+Af9HzDP/KPeg7y
MT4WaTymLewnPd/xz/yznkP8C/+i5zD/yr/qOcK/8W96jvJxPq7ne/6df9fz
A5/gE3p+5JN8Us8xPsWnIo2ntIX9oednPs2n9fzCZ/iMnl/5LJ/V8xuf43N6
jvN5Pq/nd/6T/9Rzgi/wBT0n+SJf1HOKL/GlSOMlbWF/6TnNl/mynjN8ha/o
OctX+aqec3yNr+k5z9f5up4/+W/+W88FvsE39Fzkm3xTzyW+xbcijbe0hf2j
5zLf5tt6rvAdvqPnKt/lu3qu8T2+p+c63+f7ev7mf/lfPTf4AT/Qc5Mf8kM9
t/gRP4o0PtIW9p+e2xx+IH3bvaMpOIZ3uHc1Bcf0DveepuBY3uHe1xQc2zvc
fzUFx/EO94Gm4Lje4T7UFBzPO9xHmoLje4f7pDH4P30JnvwIPOb/nZATaozB
iTiRxpicmBNrjMVJOInG2JyUk2qMw8k4mca4nJyTa4zHKTiFxvicklNGGlNq
C0ulJyGn5tR6EnEaTqMnMafltHqScDpOpycpp+f0epJxBs6gJzln5Ix6UnAm
zqQtJWfmzJHGzNrCsuhJzVk5q540nI2z6UnL2Tm7nnScg3PoSc85OaeeDJyL
c+nJyLk5t55MnIfz6MnMeTlvpDGvtrB8erJyfs6vJxsX4AJ6snNBLqgnBxfi
QnpycmEurCcXF+EienJzUS6qJw8X42J68nJxLh5pLK4trISe/FySS+opwKW4
lJ6CXJpL6ynEZbiMnsJclsvqKcLluJyeolyey+spxhW4gp7iXJErRhoragur
pKckV+bKekpxFa6ipzRX5ap6ynA1rqanLFfn6nrKcQ2uoac81+SaeipwLa6l
pyLX5tqRxtrawuroqcx1ua6eKlyP6+mpyvW5vp5q3IAb6KnODbmhnhrciBvp
qcmNubGeWtyEm+ipzU25aaSxqbawZnrqcnNurqcet+AWeupzS26ppwG34lZ6
GnJrbq2nEbfhNnoac1tuq6cJt+N2eppye24faWyvLSx872iuKXiud7gtNAW/
4R1uS03Bb3qH20pT8Nve4bbWFPyud7htNAW/7x1uW03BH3qH205T8Efe4bbX
FPyJd7hPGoND2/8ApbViug==
"]],
Annotation[#, "Geometry"]& ]}],
MouseAppearanceTag["LinkHand"]],
AllowKernelInitialization->False],
"MeshGraphics3D",
AutoDelete->True,
Editable->False,
Selectable->False],
Boxed->False,
DefaultBaseStyle->{"MeshGraphics3D", FrontEnd`GraphicsHighlightColor -> Hue[0.1, 1, 0.7]},
ImageSize->{88.5, 58.},
Lighting->{{"Ambient",
GrayLevel[0.45]}, {"Directional",
GrayLevel[0.3],
ImageScaled[{2, 0, 2}]}, {"Directional",
GrayLevel[0.33],
ImageScaled[{2, 2, 2}]}, {"Directional",
GrayLevel[0.3],
ImageScaled[{0, 2, 2}]}},
Method->{"ShrinkWrap" -> True},
ViewPoint->{1.6814053651900331`, -1.4722065688230377`, 2.5407644158056977`},
ViewVertical->{0.017108007831564867`, 0.10099131993661274`, 0.994740201944958}]\)]](https://www.wolframcloud.com/obj/resourcesystem/images/e8a/e8aa931b-1c16-46da-a12c-fcf3680c98eb/3a5379a8025c6f12.png)
![ResourceFunction["BettiNumbers"][\!\(\*
Graphics3DBox[
TagBox[
DynamicModuleBox[{Typeset`mesh = {MeshRegion, {}}},
TagBox[GraphicsComplex3DBox[CompressedData["
1:eJx1Wnl4T9cWDSIhphA/Gcg8J8Sr8qKmc6oafUQbQYsOT1NtvaeltDGPQapq
qFdqiNJWqTH01RjVc8ypVxpzaIkxCCJIImLI65e798mXdcUf9XV92zrrd+7d
e6+zzw1MGpr4bnUnJ6e+f/2nhhP/+Zt0gj9DSzut73czRh4+f+HG9GfqyFWF
C9JGXnoguk3cPjp2aUsT/1b/ZOfg3y+KxSmZvfvPiZHLLz10XrvNTd5MuD57
6opq0oqPMfFlvbt41B+aL+7+M+byhbQWsv6V6Q07jKst5zX4OnHiLGe5ZVJc
aubbLWzxPdyu/nR7SHPZ7uKQEu8iV4hvbtOz4mr8CyPHRssV5XpcjB4rqiKe
//w+9GTeSL9oOSbX4XdIuJjfWwW/Qv7RXd/0zh1bIKrQr1B/z3k3gi+8dkVU
sT8K96dyvG3/Fe4/62k9qqRd0m/R8vk3AsOy/vSWFv8TMXtb0wlx46Pli8X7
V/75L2/pOVkdfOVGDXm9pNOuqPQoueybiSPyOnhJJT6e3e2Yi8wrxyNl/K4V
jW9lNjF4l+eSnBvkRMiVg9+6XJrmMDxLR0/rem9OhFxT0/ld10iHWRfjs36o
PXeca5FAfn7uqIdx1M88AenuHoPyw6T1uwNlwvWWsbf3XxJBY9/plb8pTFr/
LlCe+vaob+3u90RClmif7BdGvztARvi3W/HE54FYeT5xxoiBofLYnfEpfd7w
N/ixNi2HPz4UIqcP31vL7xdfw3Oiesp/p8wLkR3vuc3J9fc162K8PNfztdQH
S238b52K2NYx4YRCPYyjfuaxfmeAtPI1RFrvw13F/956Lxi/qMr3/58B0nq/
gmXhhEUnc37+TfkOi300s9RfWu9pkMGPkj7rfQ80PNbv9JdW3gSadTF+luvG
1E1/f2TjH7q7jmufGtU06mEc9TOP9dY3pvc/jPNAM27lR6g8krhv/JCFxaoy
HiInnXizeFRmgcGtfA2uAg+y8Vh/B9nW5fiFr/ruyvzJWSO/dByZuifNFXSG
VIGHGp6BnTpE5C95IPD5ZrStVbx6dqnA53u5Tf6fn7o+Fvh89/vOdc11c7I9
39ebOT/s3bWa7fmmeuddaKWr2Z4vxvNzQX5+jqiHcdTPPM7Dpi2UH99XmL+N
TzdNG/5DkcL8HZfy5PTqewUK83eAW8yKQV1zFebvgIzcF9PVaYX5+01/mTDi
i6MK8xfjOe+Qn/MU9TCO+pknq7y/NtBYn9uW94l6Guvz91Z911ifV1p9SGN9
di/vHzU01merz1XXWJ8xnusq8nMdRj2Mo37mOVc4vv9P2Q6NvqJ1zbmrN/k5
NPqHy+qNzD2xHhp9wuLGh9/POeuu0Q/MW/psvbO36mns+x1Uv7U5o+tq7O8Y
z30T+bn/oh7GUT/zWHntpdFvzH8y/N6QDp4GZ99i4Q6D834Orjar7tw9jarA
3W081v9V4PyninhVBb+qQo+qQr+C56tpnxXsj6b9UbCfmvZTwf4bHJ6X4YHn
a9bFeHofNPLT+6NRD+Oon3kgfzXlkYL3X9P7ryBfNO8n5JfBIR8ND+SvWRfj
Kd818lN90KiHcdTPPFCfNdVJrG+a6hvWQ031EOtnBV653hoeqM9mXYyneq6Q
n+q/TQ/jqJ95oP9q6oMC+pem/iWg32nqdxL6o8Ghnxoe6L9mXYznfEd+6u82
PYyj/sp1w/grzm8J/kSTPwE8RJOfMTj5nyrwIBuP9XeQbV2OJz8mkJ/8m8FZ
z9PxUMMD/tnsM/hP81zAr5rnCP7W4OCHDQ/4Z7MuxvNzQX5+jqiHcdTPPHA+
MnkE5wuTd3AeMXkK5xeDw3nH8MD5yKyL8Zx3yM95inoYR/3MA+dfUyfh/Gjq
Kpw3TR2G86nB4TxreOD8a9bFeK6ryM91GPUwjvqZB+Y2pg/CfMD0TZgzmD4L
8wqDw9zD8MD8xKyL8dw3kZ/7LOphHPUzj5XXgTKvZeyRuokN5RyXL3eN/+I8
+Ux/2TMgouuRPD9Zc1tZ/cs5j2l+EmDiR/zN+Z2sDXfIv/nLnwM390pK95OL
W32dmbG8hrR8jr+JP7B+cN6+iffJB/rKYd89PB3l7ic730mYuflzF2n5qGa2
eMtv+EjXb4ccWhTvC/E+Nj3dfl+Uml/sRXqaGT3W7/Wx/d6lOetO3P7Lf4cH
dx5wb1gz83uRf9TSRp5RRT8q5D/ptm9m4qhCgfrPL0laHrDzD4X66zTd4ZaR
cEvg/nA87g/H4/6zHtx/1jOooCB570Jv2SRu3dghC0Llny3TV71zslQ0K6+H
XtLLo2xH4ZuhMnXIJ/NL/apTvfWUXQb9sXzsgRAZ0yKiX5FLTaojDpk2Kv/u
uHoVuFV3PGTmoYNnaowMNjxWnfKQBxf7Np3RMdisi/HrUz4OOzrkjkD+7W5e
nbZ3vCpQD+Oon3lStnWO/2Z7AxnpPm/5oOQoWe/X2y8d+F+GmHFzVo/tx+rL
KQlbc+PDouSkXl/eSovIFZ2eL7t5fHRdee6LM5HPvBYp3cOfmfDC5QKxMKV7
5Jm5tQmPMHj8qZ8zi2Jd5XNHHn/gmB5ueHrXqXWwfqKLnNcwcOODtuFmXYwf
vTv9771vnFPIf/b1sKj5jhsK9TCO+pmn7ZRPNwTvvykG/ueMY8D8FjJ8uaPN
2+dK1MzZtz3WXcwTc3wG7hzQtoUsuLH53WW38lXbecFxBQVXxNX7v8Zf69Jc
vnIn99VNPS6prIYj9/y+Kkd0/i6lWbFntMEjfHPC++47IRZPvLZ2fEiU4cl6
dkPBoCdHxF7X4b0mHIg062J8dMSq1x8E/eXzgf9Y7uv+hW7OGvUwjvqZx8pf
Z120IG2Qy+oY2Vi91PXstSeKcenZ52LHrjHySsP6+7pPLgK8hYyM7DF2XdJt
g6/xuph/2K15FXi0jcdaN8q2LscHbdk1MDbCWSP/wU+SI1q5u2rU83Q8xvC8
X56/npqfb4djh/0n3c6lOaGn5v0ZdendDz+ZrNWn5fnVRPN+1nU9eSj2ySHy
Pw7N+8+4xePQ/LyYx8pfh+bnW3ndivhDTYL+0zOnUCG/37zPvLtuKLXpYRz1
M4/lrwI152+zkR+dSv/wDs2fAzW//91D1vaTJ0pp/hyoOV8OJ3xWsDjRSVr+
J0Bzfhm83Df4a85H5rF8hr/m/OV1Mf7Ml4PXtKt7XiD/5YHDh3T6cZdND+Oo
n3ksfxWmuT775ja6ta+wjObzYZrr28pfV26NTncm3xaquR6+PL3/2LCvXOl+
IURz/WTc8kvBmust81j+KlhzfeZ1MT6/bfa/W88qFsi/dMdHlzrtLBCoh3HU
zzyWv4rU7Ct+GfPS1IHBhXSOitTcv26FT3EpnsHnrgjNfXBZYtH+5PXVyMeH
a+6njFt+KUxzX2Yey1+Fae7vvC7G+6U1dV458opA/lK5KC95wzGbHsZRP/NY
eR2twW8oq49Haejj1N8jNfgBuheLqAIPt/FY64bb1sV48ksK+cl3KdRTGY+y
8fDz9Xr0zJnOB28J8lGK92dvwa/JGetvC/InivdzZtHBwB2v3BXkcxTvf+uH
T3qVvVlkcH5eb5Vcbnf25H3Dw893092NtRZllph1MZ58oEZ+8pMa9TCO+pmH
8ze97/HVqY5qmnyO4vd/y0z/tctaOmnyJ4rz5fjuwPkj1j5U5GcU59f0FzPq
Tf6jyOCcjwX5S+K3hd9RzMP565T+3tLjW/MVr4vx5Mc08pN/06iHcdTPPFyf
J+jt32+Na6TJ5yiub62ed4qetKqhJn9i6uG1XXE/vuTmrsnPmPp5dMqspLmN
61bgVG87TPMZGpRdy/BwfV6Z+sPYn9JczboYT35MIT/5N4V6GEf9zMP9t3Bv
3GcrU700+Rz2pbrbiX7ZP/zmqcmfSO53pXNC72+54tDkZyT3x42Xv/rq6Oce
Bud+OmBZ0uYL3zc0PNx/N21Idr6U5w7rVsSTHxPIT/5NoB7GUT/zsA9pkpUZ
c2+9jyafY/C1h9sHJeV5a/InsjLuqcnPGHzykT7tpw5zVIF72HisdRvZ1uV4
8mMC+cm/CdTzdNzb8LB/5udLPkew/+T9IX8i2K/yfpKfEexvef8ZZz/Mz4t5
2D/z8+V1MZ78mI2f/JtCPYyjfubh8xHnL/kcc77g95/8iTmPcL6QnzHnF84v
xvm8w/nIPHw+4vzldTGe/JiNn/ybRj2Mo37m4fMv12fyOYrPj1zfyJ+wL5Vc
D8nPKD6fcv1knM+zXG+Zh8+/XJ95XYwnP6aRn/ybRj2Mo37m4bkN91/yOWY+
wP2L/ImZM3C/Iz9j5hXcHxnnuQf3U+bh+Qn3X14X48mP2fjJv2nUwzjqZx6Y
X9E5qkDAPqj975fM8z9WhvMT3XJ9u5S57z8QwK/GzFj0ed+vnXF+pSdFfVf7
09gyATpV8D96vNJrmivOr0w8/F6I97HpgX0zemB+ZX4v7L/5vcjfpbvj/va3
z9j4F2TsbDR7cDHOr7T7xoz/+TVYbdMf1/HVzxemFeD8ysTj/nA87j/rwf1n
PZC/MrvOxa+m/qtIwPsvXbc3825y5ImAfBHNm3bOmpZQXUJ+GRzyUTAP5K/g
dTE+cefLkbk1rgnkT5pW1rr4QLZND+Oon3mgPsuivp3XnV5yBuuznL01YXt2
9f0C6qGcGhHc8duACwLqp8Gh3hoeqM9mXYz/4IXutw7UL8D6LHfq/36y81wR
9guDo37mgf4r508sS9/T/jH2L/ne0b3NWx2/h/1ORq/J6Da61k0F/dHg0E8N
D/Rfsy7GJzX5euGanjU08rudSHhjxXMuGvUwjvqZB/yVXBPf99qYLQ8V+BM5
dpnve9dfvgu4p+zT5YOdVx9fMzj5nypwDxsP+Svbuhx/c9w/2rjMqa6Rf377
xyVOI2tq1PN03NvwgH+Wg1/rkDZg90EF/lO6fBa/w9ExG/2qDBHJN5N/uYr+
1uDghw0P+GdYtyL+uY+6RO+YeF0h/4eba/sem3NXoR7GUT/zwPlI7v7l2VWn
DtwXcL6QJW1i529a4CThPCK/Lczru2FiDQnnlwq88nnH8MD5yKyL8WHBd7vP
1Dfx/CWnUX1APYyjfuaB86+c5DSm1aP4ivkV17fsV/ufietfMb/iejjJUX/p
850r5ldcPxmH86xgHjj/Cl4X43v2Ehv/faVIIL/TyVMRyY6K+RXrYRz1Mw/M
N1SWj0vgA9c8AfMB079gnqCuxYYuntL+kYD5g8FhXmF4YL5h1sX4zGovDO97
6Tcb/8/XSjJ7LdmF8xaDo37mgfkV+w2c/3Afx3kR+wGcLwEebuOB+ZVZF+PJ
L9n4yXfZ9FTGo2w8MJ/U5KMUzPc0PRcF80BNPkfB/NDgMG80PDCfNOtiPPlA
jfzkJzXqYRz1Mw/MnzX5HAXzW03+RMG8V5OfUTAfNjjMkw0PzJ/NuhhPfszG
T/5Nox7GUT/zwP2CJp+D83lN/gTn+Zr8DM7/K/DK9wWGB+4XzLoYT35MIT/5
N4V6GEf9zAP3R5p8joD7F03+RMJ9jSY/I+F+x+BwH2R44P4I1q2IJz+G91Oa
/JtAPYyjfuZhH0L3g5p8jsHpfk2TP5GV8b/2x/IzBqf7uyrwaBsP3Q/a1uV4
8mMC+cm/CdTzdDzG8MD9ryafI+D+VJM/EXDfqsnPCLifNTjc5xoeuP8162I8
+TG8X9bk3/A+2uCon3ngfl+Tz8H7cU3+BO/TNfkZvH83ONzXGx643zfrYjz5
MY385N806mEc9TMPfL+hyeco+P5Bkz9R8L2EJj+j4PsKg8P3GIYHvt8w62I8
+TGN/OTfNOphHPUzD3x3pMnn4PctmvwJfiejyc/g90IGh+92DA98/2PWxXju
18hP/s2mh3HUzzz/B7JHQA8=
"],
{Hue[0.6, 0.3, 0.85], EdgeForm[Hue[0.6, 0.3, 0.75]], EdgeForm[None], Specularity[
GrayLevel[0.2], 30],
TagBox[Polygon3DBox[CompressedData["
1:eJxN2mfUz/Ufx/Hsvffee++9994zZIWskBWyQlYo0i6VrJAVskJ2yqi0hKyQ
FbJCf5/zfzjne+N13o/Pde9557rxPb8c3Z9vOTDmU089tSr2U0/FenxjPF54
x7Lg2BxuHAuOy+HGs+D4HG4CC07I4Say4MQcbhILTsrhJrPg5BxuCgtOyeGm
suDUnFpfDI5pafTE5rScVk9cTsfp9MTn9JxeT0LOwBn0JOaMnFFPUs7EmfQk
58ycWU9KzsJZ9KTmrJw10phVW1g2PWk5O2fXk45zcA496Tkn59STgXNxLj0Z
OTfn1pOJ83AePZk5L+fVk4XzcT49WTk/54805tcWVkBPdi7IBfXk4EJcSE9O
LsyF9eTiIlxET24uykX15OFiXExPXi7OxfXk4xJcQk9+LsklI40ltYWV0lOQ
S3NpPYW4DJfRU5jLclk9Rbgcl9NTlMtzeT3FuAJX0FOcK3JFPSW4ElfSU5Ir
c+VIY2VtYVX0lOaqXFVPGa7G1fSU5epcXU85rsE19JTnmlxTTwWuxbX0VOTa
XFtPJa7DdfRU5rpcN9JYV1tYPT1VuT7X11ONG3ADPdW5ITfUU4MbcSM9Nbkx
N9ZTi5twEz21uSk31VOHm3EzPXW5OTePNDbXFtZCT31uyS31NOBW3EpPQ27N
rfU04jbcRk9jbstt9TThdtxOT1Nuz+31NOMO3EFPc+7IHSONHbWFPa2nJXfi
TnpacWfurKc1d+EuetrwM/yMnrbclbvqacfduJue9tydu+vpwD24h56O3JN7
Rhp7agt7Vk8n7sW99HTm3txbTxfuw330PMPP8XN6unJf7qunG/fjfnq6c3/u
r6cHD+ABenryQB4YaRyoLex5Pb14EA/S05sH82A9fXgID9HzHL/AL+jpy0N5
qJ5+PIyH6enPw3m4ngE8gkfoGcgjeWSkcaS2sBf1DOJRPErPYB7No/UM4TE8
Rs8L/BK/pGcoj+WxeobxOB6nZziP5/F6RvAEnqBnJE/kiZHGidrCXtYziifx
JD2jeTJP1jOGp/AUPS/xK/yKnrE8lafqGcfTeJqe8Tydp+uZwDN4hp6JPJNn
Rhpnagt7Vc8knsWz9Ezm2TxbzxSew3P0vMKv8Wt6pvLr/LqeaTyX5+qZzvN4
np4Z/Aa/oWcmz+f5kcb52sLe1DOL3+K39Mzmt/ltPXP4HX5Hz2v8Lr+r53V+
j9/TM5ff5/f1zOMP+AM9b/CH/KGe+byAF0QaF2gL+0jPW/wxf6znbf6EP9Hz
Di/khXre5U/5Uz3v8SJepOd9XsyL9XzAS3iJng95KS/Vs4CX8bJI4zJtYZ/p
+ZiX83I9n/AKXqFnIa/klXo+5c/5cz2LeBWv0rOYV/NqPUt4Da/Rs5TX8lo9
y3gdr4s0rtMW9oWe5bye1+tZwRt4g56VvJE36vmcv+Qv9aziTbxJz2rezJv1
rOEtvEXPWt7KW/Ws4228LdK4TVvYV3rW83bermcD7+AdejbyTt6p50v+mr/W
s4l38S49m3k379azhffwHj1beS/v1bON9/G+SOM+bWEx9GznWBxLzw6Ow3H0
7OR4HE/P15yAE+jZxYk4kZ7dnIST6NnDyTiZnr2cglPo2cepOFWkMZW2/Y93
4PG+seCDHO63Fvwdh3vIgg9zuEcs+CiH+70F/8Dh/mjBxzjcnyz4Zw73Fwv+
lcP9zYKP83F9+/mA/a7nIJ/gE3q+45N8Us9hPsWn9BzlP/gPPT/waT6t5xif
4TN6fuazfFbPr3yOz+k5zuf5fKTxvLawP/Wc4At8Qc9JvsgX9ZziS3xJzx/8
F/+l5zRf5st6zvAVvqLnLF/lq3rO8TW+puc8X+frkcbr2sL+1nOBb/ANPRf5
Jt/Uc4lv8S09f/E//I+ey3ybb+u5wnf4jp6rfJfv6rnG9/ienut8n+9HGu9r
C/tXzw1+wA/03OSH/FDPLX7Ej/T8w//xf3puc/jHcdu9oyk4hne4dzUFx/QO
956m4Fje4d7XFBzbO9wnjcH/6osT4/89Dziud7gPNQXH8w73kabg+N7h/qcp
OIF3gicfvf0tISfUGIMTcSKNMTkxJ9YYi5NwEo2xOSknjTQGx7FkGuNyck6u
MR6n4BQa43NKTqknAafiVHoScmpOrScRp+E0ehJzWk6rJwmn43TaknJ6Th9p
TK8tLIOe5JyRM+pJwZk4k56UnJkz60nFWTiLntSclbPqScPZOJuetJyds+tJ
xzk4h570nJNzRhpzagvLpScj5+bcejJxHs6jJzPn5bx6snA+zqcnK+fn/Hqy
cQEuoCc7F+SCenJwIS6kJycX5sKRxsLaworoyc1FuaiePFyMi+nJy8W5uJ58
XIJL6MnPJbmkngJcikvpKcilubSeQlyGy+gpzGW5bKSxrLawcnqKcnkur6cY
V+AKeopzRa6opwRX4kp6SnJlrqynFFfhKnpKc1WuqqcMV+Nqespyda4eaayu
LayGnvJck2vqqcC1uJaeilyba+upxHW4jp7KXJfr6qnC9bienqpcn+vrqcYN
uIGe6tyQG0YaG2oLa6SnJjfmxnpqcRNuoqc2N+WmeupwM26mpy435+Z66nEL
bqGnPrfklnoacCtupacht+bWkcbW2sLa6GnMbbmtnibcjtvpacrtub2eZtyB
O+hpzh25o54W/DQ/racld+JOelpxZ+6spzV34S6Rxi7awp7R05a7clc97bgb
d9PTnrtzdz0duAf30NORe3JPPU/zs/ysnk7ci3vp6cy9ubeeLtyH+0Qa+2gL
e05PV+7LffV0437cT0937s/99fTgATxAT08eyAP1PMvP8/N6evEgHqSnNw/m
wXr68BAeEmkcoi3sBT19eSgP1dOPh/EwPf15OA/XM4BH8Ag9A3kkj9TzPL/I
L+oZxKN4lJ7BPJpH6xnCY3hMpHGMtrCX9AzlsTxWzzAex+P0DOfxPF7PCJ7A
E/SM5Ik8Uc+L/DK/rGcUT+JJekbzZJ6sZwxP4SmRxinawl7RM5an8lQ943ga
T9MznqfzdD0TeAbP0DORZ/JMPS/zq/yqnkk8i2fpmcyzebaeKTyH50Qa52gL
C987pmoK/sY73Gmagr/1Dne6puBD3uHO0BR8xDvcmZqCv/cO91VNwT96hztL
U/BP3uHO1hT8i3e4czQF/+Yd7pPG4ND22mO//nhzLXgeh/uGBc/ncN+04Lc4
3Lct+B0O910Lfo/Dfd+CP+BwP7TgBRzuRxb8MYf7iQUv5HBfs4Xawj7VM48X
8SI983kxL9bzFi/hJXre4aW8VM97vIyX6fmAP+PP9Czg5bxcz8e8glfoWcgr
eWWkcaW2sM/1LOJVvErPYl7Nq/Us4TW8Rs9SXstr9SzjdbxOz2f8BX+hZzmv
5/V6VvAG3qBnJW/kjZHGjdrCvtSzijfxJj2reTNv1rOGt/AWPWt5K2/Vs463
8TY9X/BX/JWe9bydt+vZwDt4h56NvJN3Rhp3agv7Ws8m3sW79Gzm3bxbzxbe
w3v0bOW9vFfPNt7H+/R8xft5v57tfIAP6NnB3/A3enbyQT4YaTyoLexbPbv4
O/5Oz24+xIf07OHDfFjPXj7CR/Ts46N8VM9+/p6/13OAf+Af9HzDP/KPeg7y
MT4WaTymLewnPd/xz/yznkP8C/+i5zD/yr/qOcK/8W96jvJxPq7ne/6df9fz
A5/gE3p+5JN8Us8xPsWnIo2ntIX9oednPs2n9fzCZ/iMnl/5LJ/V8xuf43N6
jvN5Pq/nd/6T/9Rzgi/wBT0n+SJf1HOKL/GlSOMlbWF/6TnNl/mynjN8ha/o
OctX+aqec3yNr+k5z9f5up4/+W/+W88FvsE39Fzkm3xTzyW+xbcijbe0hf2j
5zLf5tt6rvAdvqPnKt/lu3qu8T2+p+c63+f7ev7mf/lfPTf4AT/Qc5Mf8kM9
t/gRP4o0PtIW9p+e2xx+IH3bvaMpOIZ3uHc1Bcf0DveepuBY3uHe1xQc2zvc
fzUFx/EO94Gm4Lje4T7UFBzPO9xHmoLje4f7pDH4P30JnvwIPOb/nZATaozB
iTiRxpicmBNrjMVJOInG2JyUk2qMw8k4mca4nJyTa4zHKTiFxvicklNGGlNq
C0ulJyGn5tR6EnEaTqMnMafltHqScDpOpycpp+f0epJxBs6gJzln5Ix6UnAm
zqQtJWfmzJHGzNrCsuhJzVk5q540nI2z6UnL2Tm7nnScg3PoSc85OaeeDJyL
c+nJyLk5t55MnIfz6MnMeTlvpDGvtrB8erJyfs6vJxsX4AJ6snNBLqgnBxfi
QnpycmEurCcXF+EienJzUS6qJw8X42J68nJxLh5pLK4trISe/FySS+opwKW4
lJ6CXJpL6ynEZbiMnsJclsvqKcLluJyeolyey+spxhW4gp7iXJErRhoragur
pKckV+bKekpxFa6ipzRX5ap6ynA1rqanLFfn6nrKcQ2uoac81+SaeipwLa6l
pyLX5tqRxtrawuroqcx1ua6eKlyP6+mpyvW5vp5q3IAb6KnODbmhnhrciBvp
qcmNubGeWtyEm+ipzU25aaSxqbawZnrqcnNurqcet+AWeupzS26ppwG34lZ6
GnJrbq2nEbfhNnoac1tuq6cJt+N2eppye24faWyvLSx872iuKXiud7gtNAW/
4R1uS03Bb3qH20pT8Nve4bbWFPyud7htNAW/7x1uW03BH3qH205T8Efe4bbX
FPyJd7hPGoND2/8ApbViug==
"]],
Annotation[#, "Geometry"]& ]}],
MouseAppearanceTag["LinkHand"]],
AllowKernelInitialization->False],
"MeshGraphics3D",
AutoDelete->True,
Editable->False,
Selectable->False],
Boxed->False,
DefaultBaseStyle->{"MeshGraphics3D", FrontEnd`GraphicsHighlightColor -> Hue[0.1, 1, 0.7]},
ImageSize->{90., 75.},
Lighting->{{"Ambient",
GrayLevel[0.45]}, {"Directional",
GrayLevel[0.3],
ImageScaled[{2, 0, 2}]}, {"Directional",
GrayLevel[0.33],
ImageScaled[{2, 2, 2}]}, {"Directional",
GrayLevel[0.3],
ImageScaled[{0, 2, 2}]}},
Method->{"ShrinkWrap" -> True},
ViewPoint->{0.6822353187716305, -1.7228455869138901`, 2.831317370672511},
ViewVertical->{-0.06483572623149177, 0.04946101955110243, 0.9966694216985893}]\)]](https://www.wolframcloud.com/obj/resourcesystem/images/e8a/e8aa931b-1c16-46da-a12c-fcf3680c98eb/55073ec5033eca70.png)
![ResourceFunction["BettiNumbers"][\!\(\*
Graphics3DBox[
TagBox[
DynamicModuleBox[{Typeset`mesh = {MeshRegion, {}}},
TagBox[GraphicsComplex3DBox[CompressedData["
1:eJx1lX1Mk3cQxxthTEPQbZZMthllIjiRl2ROBJVz7EEFMyW8uRkDWtGZKKIs
KmTBjTgTF2Vz0Q2LC1XIBMFFrAKi0UOKE1wp0ArMAa1IK6tt15aCQRth0zzX
ZEf8Jf3nm8vnud7L9wJlOcnbpkgkkqT/fl4Seg9Awl5JoLbtqUYPTet0B4XX
mmFfSuUXvj5XsLrqxXs8KV5+ouPzI7vMkK6zRX9zuAOcAUcNDcoSMX54UvyH
vpsetV51wtqJvYszpvZQvBg3Npmvblesv/4EIPRJ+PKj/ZQPnH0zpbo7pBek
jcnZmms6SDJHRNl/V+Hmr9Z862oxQcRWv66WCgP4R/2UcDKjCh3ZQ0r3cxvM
98oq3XLXRDqsjFQ5CgNcoEz9WKtvtBAH3pZuKBrpvQdluErWWdsHEr0QGj69
DU9hX46/9wPwVb07ttr3EaSZw3JbMy5j0KifPLLEBEKwFCqu20iHmoXQtDbS
Aij4fOJVN0wcUGgzd+uL7sACc1pb4ZyHkLFxn/e8di3+Gnv4mPBeJ9T3jri/
S30MBXm/1IRLG9B94q8B+d5umDeU4N8qOEkX8+2FnZvliz7NHCWOp47vyBrV
NReNoF729fbSM91I+uW5K4XjMVbY9my8vyD0pkc/Zzf01z90ku7huDQKeUjl
KHFgvOd4psv2B1ZvzItPLjBB5Ujx6QOD99EgvXpluLsTl15Iy2//0gJ7xmbc
WB93C2/dqGiw1HXh4EF5enCtg3Qo21580/jzfawKOeLIqnERB2Y8K08AaT82
h6sS3/AyQvaiFbPnHupDqyn2B7VsAC8p3V0TtiFw5ep2+E9RYYemOj9/mRFL
lyzeYv/TQjrU1s/KCpYO4bFru6x6lZ044ndMuDPqUGGSxgATqcLM6Tl6TFHE
rXr/+78xeE+0KqhnACaKwmTTEptxPMHmUC+1YLFwKT7wziDpIseGPgEftMyu
NxEH9seme5/3s+JnRXVua4wWNhkjTgadNmBnmWKrtdyGz+co8/6J08GKU3dl
s966jWGvm5siYuxYrvxt1J54j3Ro/ijgx+gdDlwdfz7XmdxFHLEvDk/fxH1G
rqe9fLdfpb+Kw7+LlD/LEyl/9r9I53UgDq8bUv1ZnZHqz/qC/6+/p4/E4X1H
mh82J0jzw+aKdD6HxOFzizT/bM6R5p/tBel8j4jD9w75/op7inx/xb1Gvr+i
DxCH+waS/zCfQfIf5kukcx8jDvc9JP9kPonkn8xXSec+TBzu20j+z3weyf/Z
XSCd3xHiALs7SHeQ3S+ke8fuIOnA7ilx4F9+PaXA
"],
{Hue[0.6, 0.3, 0.85], EdgeForm[Hue[0.6, 0.3, 0.75]],
TagBox[Polygon3DBox[CompressedData["
1:eJwNw22SgQAAAFD6pCiKoigVRVEURVEURVFmj+AC+3ePv97Mkz6/Px+gVqv9
fYPfdQAEAQiEYBhCYARFkQbQhKAmBmEIguEI3mjgrWYbw9oERuA4QeJkq0V2
2l2C6FIERZIUTdKdDt3r9imqz1AMTTMszfZ67KA/ZJghx3Asy/EsPxjwo+GY
48YCJ/C8IPLiaCROxpIgSLIgi6KsiMpkokylmSzPVFlVFFVTtOlUm88WqrrQ
VV3TdEMz5nNjuVjp+srUTcMwLcNaLq31amOaG9u0Lct2LGe9drabnW3vXNt1
HNdzvO3W2+8OrnvwXd/z/MAL9vvgeDj5/in0wyAIoyA6HqPz6RKGlziMoyhO
ouR8Tq6XWxzf0jhNkjRLsus1u98eafrI0zzL8iIr7vfi+Xjl+avMy6Ioq6J6
Pqv3Cy1LFC7hqoLBCny/wfo/7es7Hg==
"]],
Annotation[#, "Geometry"]& ]}],
MouseAppearanceTag["LinkHand"]],
AllowKernelInitialization->False],
"MeshGraphics3D",
AutoDelete->True,
Editable->False,
Selectable->False],
Boxed->False,
DefaultBaseStyle->{"MeshGraphics3D", FrontEnd`GraphicsHighlightColor -> Hue[0.1, 1, 0.7]},
Lighting->{{"Ambient",
GrayLevel[0.45]}, {"Directional",
GrayLevel[0.3],
ImageScaled[{2, 0, 2}]}, {"Directional",
GrayLevel[0.33],
ImageScaled[{2, 2, 2}]}, {"Directional",
GrayLevel[0.3],
ImageScaled[{0, 2, 2}]}},
Method->{"ShrinkWrap" -> True},
ViewPoint->{0.6170728023368904, -2.2455895182375367`, 2.4549030270456313`},
ViewVertical->{-0.0685409011812995, 0.04920995157462706, 0.9964339042461765}]\)]](https://www.wolframcloud.com/obj/resourcesystem/images/e8a/e8aa931b-1c16-46da-a12c-fcf3680c98eb/31a9b37bac575b69.png)
![ResourceFunction["BettiNumbers"][\!\(\*
Graphics3DBox[
TagBox[
DynamicModuleBox[{Typeset`mesh = {MeshRegion, {}}},
TagBox[GraphicsComplex3DBox[CompressedData["
1:eJytlTtLA1EQhRe1sdFC7WzEWi0DNhOCjTYGH4USUgRsjY0oiPgD1EZ8FGov
PsBSBBlBsLWwsxK32sY8SMQIvjMzsGedzoFtzr2Ze/jm3Ju+QnFiriUIguz3
1xpolSmA+pwa6eooPlM2GkqVbu9tffq36sn9mwOF9rEa9aR2RrfzD7Z+cvxT
b4n9a5WLy/Vcg+Yz72e9K4+4nv7bz4f4CW3/UW1vfymMKD+72NZ/92T6wmvn
1XimQqvLB+eD3ZHpGy+Tp+FWnQ53b3LDMyXo05A+VdO1r56juvbVc1TXvnpO
vE+V9BzVla/yVl05KlfVlZfyi/cJSTkhv2Yl5+zN05ubVBr8s+OfHf/s+Gf0
L/zZ4c8Of3b4M/KXvuzkh538sJMfxvwIF8Z7JFwY74twYbwXwoUx/80qMw5I
5prQZa4JXeoaBfBvvwP/poN/jvcx/6YDf9OBv+nAH/oYf9MhP6ZDfkyH/EAf
y4/pkH/TIf+mQ/6hj+Xfmc//zxneH/RPjn9y/BP6h/cT+ZPDnxz+hPzh/cf8
kJMfcvJDmB/4H8T8k5N/cvJPmP8v+XxaeQ==
"],
{Hue[0.6, 0.3, 0.85], EdgeForm[Hue[0.6, 0.3, 0.75]],
TagBox[Polygon3DBox[CompressedData["
1:eJwNw22SgQAAAFD6QlEURVEqiqIoiqJSFEWZPYIL7N89/nozT/z8/nyAWq32
9w1+1wEQBCAQgmEIgZFGA2kCLQhqoRCKICiGYM0m1m51ULSDoziG4QRGtNtE
t9PD8R6JkwRBUgTV7VL93oAkBzRJUxTNUEy/zwwHI5oesTTLMCzHcMMhNx5N
WHbCszzH8QInjMfCdCLyvCjxkiBIsiBPp/JMnEvSXJEUWVZUWZ3N1MV8qShL
TdFUVdNVfbHQV8u1pq0NzdB1w9TN1crcrLeGsbUMyzQt27Q3G3u33VvW3rEc
23Zc293t3MP+6DhHz/Fc1/Nd/3DwT8ez550DL/D9IPTD0ymMzpcguMRBHIZx
EiZRlFwvtzi+pXGaJGmWZNdrdr890vSRp3mW5UVW3O/F8/HK81eZl0VRVkX1
fFbvV70s62AJVhUIV/D7DTf+Ae0TOxg=
"]],
Annotation[#, "Geometry"]& ]}],
MouseAppearanceTag["LinkHand"]],
AllowKernelInitialization->False],
"MeshGraphics3D",
AutoDelete->True,
Editable->False,
Selectable->False],
Boxed->False,
DefaultBaseStyle->{"MeshGraphics3D", FrontEnd`GraphicsHighlightColor -> Hue[0.1, 1, 0.7]},
Lighting->{{"Ambient",
GrayLevel[0.45]}, {"Directional",
GrayLevel[0.3],
ImageScaled[{2, 0, 2}]}, {"Directional",
GrayLevel[0.33],
ImageScaled[{2, 2, 2}]}, {"Directional",
GrayLevel[0.3],
ImageScaled[{0, 2, 2}]}},
Method->{"ShrinkWrap" -> True},
ViewPoint->{1.3, -2.4, 2.},
ViewVertical->{0., 0., 1.}]\)]](https://www.wolframcloud.com/obj/resourcesystem/images/e8a/e8aa931b-1c16-46da-a12c-fcf3680c98eb/6a89afc358d7ded0.png)

![BinaryDeserialize[
BaseDecode[
"ODpmBnMSQ29tcG91bmRFeHByZXNzaW9uZgJzClNldERlbGF5ZWRmAWYCcw9HbG9iYWxgaW5jbHVkZVFmAHMFQmxhbmtmAHMFQmxhbmtmAXMFQmxhbmtzBVBvaW50cwRUcnVlZgJzClNldERlbGF5ZWRmAWYCcw9HbG9iYWxgaW5jbHVkZVFmAnMHUGF0dGVybnMNR2xvYmFsYHBvaW50c2YAcwVCbGFua2YCcwdQYXR0ZXJucwhHbG9iYWxgdGYAcwVCbGFua2YBZgBzBUJsYW5rZgJzB1BhdHRlcm5zC0dsb2JhbGBsaXN0ZgBzBUJsYW5rZgFzBVRydWVRZgJzBExlc3NmAXMDTWF4ZgNzBUFwcGx5ZgFzCEZ1bmN0aW9uZgJzEUV1Y2xpZGVhbkRpc3RhbmNlZgFzBFNsb3RDAmYBcwRTbG90QwFmAnMHU3Vic2V0c2YCcwRQYXJ0cw1HbG9iYWxgcG9pbnRzcwtHbG9iYWxgbGlzdGYBcwRMaXN0QwJmAXMETGlzdEMBcwhHbG9iYWxgdGYCcwpTZXREZWxheWVkZgFzE0dsb2JhbGBncm91cERpc3BsYXlmAnMHUGF0dGVybnMLR2xvYmFsYG1lc2hmAHMFQmxhbmtmA3MER3JpZGYCcwpNYXBJbmRleGVkZgFzCEZ1bmN0aW9uZgNzBExpc3RmAnMJU3Vic2NyaXB0cwhHbG9iYWxgSGYCcwRQbHVzZgFzBUZpcnN0ZgFzBFNsb3RDAkP/UwUg4omFIGYGcwVXaGljaGYCcwVFcXVhbGYBcwRTbG90QwFDAGYBcwRMaXN0QwBmAnMJTGVzc0VxdWFsZgFzBFNsb3RDAUMDZgFzA1Jvd2YCcwZSaWZmbGVmAnMNQ29uc3RhbnRBcnJheXMKR2xvYmFsYO+evWYBcwRTbG90QwFTBSDiipUgcwRUcnVlZgJzC1N1cGVyc2NyaXB0cwpHbG9iYWxg7569ZgFzBFNsb3RDAWYBcxNHbG9iYWxgQmV0dGlOdW1iZXJzcwtHbG9iYWxgbWVzaGYCcwRSdWxlcwhTcGFjaW5nc0MAZgJzBFJ1bGVzCUFsaWdubWVudGYCcwRMaXN0ZgNzBExpc3RzBVJpZ2h0cwZDZW50ZXJzBExlZnRzCUF1dG9tYXRpY2YCcwpTZXREZWxheWVkZgNzDkdsb2JhbGBkZWxNZXNoZgJzB1BhdHRlcm5zC0dsb2JhbGBzZWVkZgBzBUJsYW5rZgJzB1BhdHRlcm5zDEdsb2JhbGBjb3VudGYAcwVCbGFua2YCcwdQYXR0ZXJucwpHbG9iYWxgZGltZgBzBUJsYW5rZgJzA1NldGYDcw5HbG9iYWxgZGVsTWVzaHMLR2xvYmFsYHNlZWRzDEdsb2JhbGBjb3VudHMKR2xvYmFsYGRpbWYCcxJDb21wb3VuZEV4cHJlc3Npb25mAXMKU2VlZFJhbmRvbXMLR2xvYmFsYHNlZWRmAXMMRGVsYXVuYXlNZXNoZgJzClJhbmRvbVJlYWxmAnMETGlzdEMAQwFmAnMETGlzdHMMR2xvYmFsYGNvdW50cwpHbG9iYWxgZGltZgJzClNldERlbGF5ZWRmBHMOR2xvYmFsYGRpc3BsYXlmAnMHUGF0dGVybnMLR2xvYmFsYHNlZWRmAHMFQmxhbmtmAnMHUGF0dGVybnMMR2xvYmFsYGNvdW50ZgBzBUJsYW5rZgJzB1BhdHRlcm5zCkdsb2JhbGBkaW1mAHMFQmxhbmtmAnMHUGF0dGVybnMIR2xvYmFsYHRmAHMFQmxhbmtmAnMGTW9kdWxlZgRzBExpc3RzC0dsb2JhbGBtZXNocw1HbG9iYWxgcG9pbnRzcwxHbG9iYWxgZmFjZXNzDEdsb2JhbGBhbHBoYWYFcxJDb21wb3VuZEV4cHJlc3Npb25mAnMDU2V0cwtHbG9iYWxgbWVzaGYDcw5HbG9iYWxgZGVsTWVzaHMLR2xvYmFsYHNlZWRzDEdsb2JhbGBjb3VudHMKR2xvYmFsYGRpbWYCcwNTZXRzDUdsb2JhbGBwb2ludHNmAXMPTWVzaENvb3JkaW5hdGVzcwtHbG9iYWxgbWVzaGYCcwNTZXRzDEdsb2JhbGBmYWNlc2YBcwdGbGF0dGVuZgJzBVRhYmxlZgJzCU1lc2hDZWxsc3MLR2xvYmFsYG1lc2hzCEdsb2JhbGBpZgNzBExpc3RzCEdsb2JhbGBpQwBmAnMEUGx1c3MKR2xvYmFsYGRpbUMBZgJzA1NldHMMR2xvYmFsYGFscGhhZgJzCk1lc2hSZWdpb25zDUdsb2JhbGBwb2ludHNmAnMGU2VsZWN0cwxHbG9iYWxgZmFjZXNmAnMPR2xvYmFsYGluY2x1ZGVRcw1HbG9iYWxgcG9pbnRzcwhHbG9iYWxgdGYBcw9UcmFkaXRpb25hbEZvcm1mAnMER3JpZGYBcwRMaXN0ZgJzBExpc3RzDEdsb2JhbGBhbHBoYWYBcxNHbG9iYWxgZ3JvdXBEaXNwbGF5cwxHbG9iYWxgYWxwaGFmAnMEUnVsZXMJQWxpZ25tZW50ZgJzBExpc3RzCUF1dG9tYXRpY3MDVG9wcwROdWxs"]];
Manipulate[
display[seed, count, dimension, \[Alpha]],
{{\[Alpha], 0.418, "distance parameter (\[Alpha])"}, 0, 1, Appearance -> "Labeled"},
{{count, 18, "number of points"}, 4, 50, 1, Appearance -> "Labeled"},
{dimension, {2, 3}},
{{seed, 32, "random seed"}, 1, 100, 1, Appearance -> "Labeled"},
SaveDefinitions -> True
]](https://www.wolframcloud.com/obj/resourcesystem/images/e8a/e8aa931b-1c16-46da-a12c-fcf3680c98eb/306f8b634ce263dc.png)
![dialog = StringCases[
StringReplace[StringTake[ResourceData["Hamlet"], {828, 949}], "Bernardo" :> "Birdnardo"], {"Ber.\n" ~~ Shortest[line__] ~~ "\n" :> ResourceFunction["BirdSay"][line], "Fran.\n" ~~ Shortest[line__] ~~ "\n" :> ResourceFunction["WolfieSay"][line, Right]}]](https://www.wolframcloud.com/obj/resourcesystem/images/e8a/e8aa931b-1c16-46da-a12c-fcf3680c98eb/19f8fd684f2d3e3a.png)