Wolfram Function Repository
Instant-use add-on functions for the Wolfram Language
Function Repository Resource:
Return the fold that maps two points to two lines
ResourceFunction["BelochFold"][{p1,l1},{p2,l2}] returns the fold(s) that maps points p1 and p2 to lines l1 and l2. |
Find the fold that maps the two given points to the y and x axes:
| In[1]:= | ![{p1, p2} = {{-4, 1}, {-2, 2}};
{yaxis, xaxis} := {{{0, 0}, {0, 1}}, {{0, 0}, {1, 0}}};
folds = ResourceFunction["BelochFold"][{p1, yaxis}, {p2, xaxis}][[
1]] // RootReduce](https://www.wolframcloud.com/obj/resourcesystem/images/e81/e81b2484-9131-4fff-afc1-6494c9dfcf02/03eb8cd931a75427.png) |
| Out[3]= |
With this fold, show the origami solution to the duplication of the cube problem:
| In[4]:= | ![cube2 = (folds[[1]] + #) & /@ {{0, 0}, {1, 0}, {1, 2^(1/3)}};
newpoints = ResourceFunction["ReflectPoints"][#, {p1, p2}] & /@ {folds};
Graphics[{ {Black, Dashed, InfiniteLine@folds},
AbsolutePointSize[5], EdgeForm[Black],
Line[{{-4, 0}, {3, 0}}], Line[{{0, -3}, {0, 4}}],
{Blue, Line[cube2]},
Style[Text[1, Mean[Take[cube2, 2]] - {0, .3}], 14],
Style[Text[2^(1/3), Mean[Take[cube2, -2]] + {.3, 0}], 14],
Text[#, # + {0, .2}] & /@ {p1, p2},
Red, Point[{p1, p2}], Green, Point /@ newpoints}]](https://www.wolframcloud.com/obj/resourcesystem/images/e81/e81b2484-9131-4fff-afc1-6494c9dfcf02/49b2662720ced884.png) |
| Out[5]= | 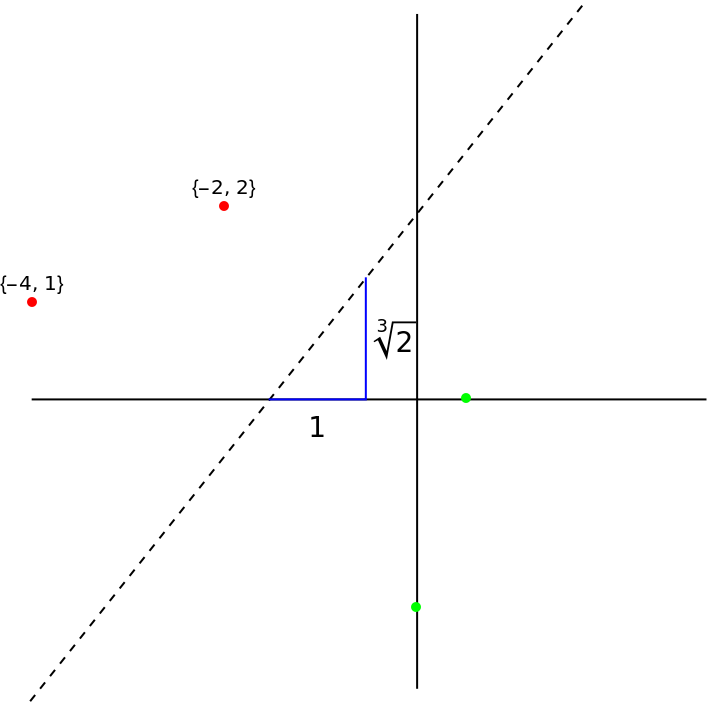 |
Find the folds that map two points to the y and x axes:
| In[6]:= | ![{p1, p2} = {{-Sqrt[3], -1}, {Sqrt[3], 1}};
{yaxis, xaxis} := {{{0, 0}, {0, 1}}, {{0, 0}, {1, 0}}};
folds = ResourceFunction["BelochFold"][{p1, yaxis}, {p2, xaxis}] // RootReduce](https://www.wolframcloud.com/obj/resourcesystem/images/e81/e81b2484-9131-4fff-afc1-6494c9dfcf02/0b239896bbc3a637.png) |
| Out[8]= |
Show the origami steps to fold a regular nonagon:
| In[9]:= | ![newpoints = ResourceFunction["ReflectPoints"][#, {p1, p2}] & /@ folds; Graphics[{ {Black, Dashed, InfiniteLine@# & /@ folds, LightGray,
InfiniteLine@(# {-1, 1}) & /@ folds, Cyan,
InfiniteLine@# & /@ Subsets[CirclePoints[3]/Cos[\[Pi]/3], {2}]},
AbsolutePointSize[5], EdgeForm[Black], {White, Polygon[CirclePoints[9]/Cos[\[Pi]/9]]},
Line[{{-4, 0}, {3, 0}}], Line[{{0, -3}, {0, 4}}],
Text[#, # + {0, .2}] & /@ {p1, p2},
Red, Point[{p1, p2}], Green, Point /@ newpoints}]](https://www.wolframcloud.com/obj/resourcesystem/images/e81/e81b2484-9131-4fff-afc1-6494c9dfcf02/4f3a252b0b7acde2.png) |
| Out[9]= | 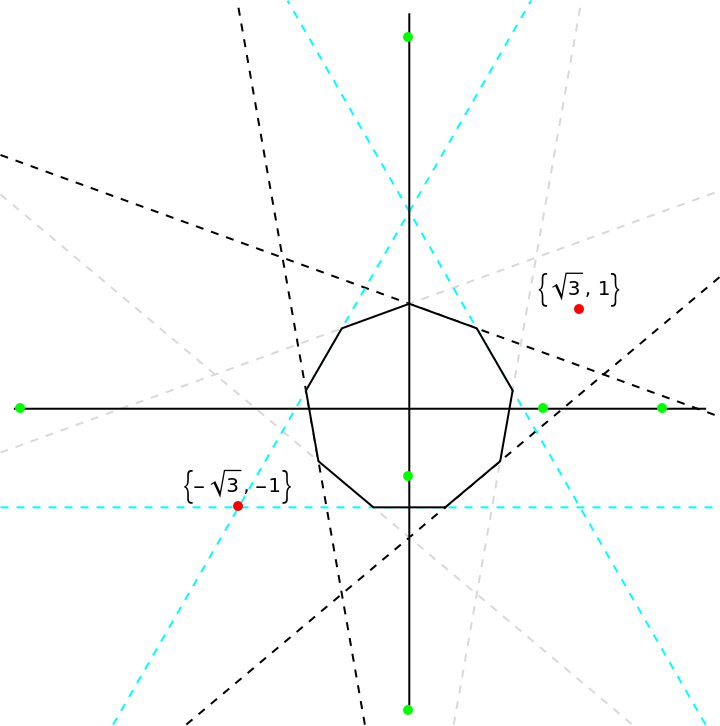 |
Find the fold that map the two given points to the y and x axes:
| In[10]:= | ![{p1, p2} = {{-2, 0}, {-1, 2}};
{yaxis, xaxis} := {{{0, 0}, {0, 1}}, {{0, 0}, {1, 0}}};
folds = ResourceFunction["BelochFold"][{p1, yaxis}, {p2, xaxis}][[
1]] // RootReduce](https://www.wolframcloud.com/obj/resourcesystem/images/e81/e81b2484-9131-4fff-afc1-6494c9dfcf02/7ffcda119e893bc4.png) |
| Out[11]= |
With this fold, show the origami solution for the plastic constant:
| In[12]:= | ![rho = First[m /. Solve[m^3 == m + 1]];
plastic = (folds[[1]] + #) & /@ {{0, 0}, {1, 0}, {1, rho}};
newpoints = ResourceFunction["ReflectPoints"][#, {p1, p2}] & /@ {folds};
Graphics[{ {Black, Dashed, InfiniteLine@folds},
AbsolutePointSize[5], EdgeForm[Black],
Line[{{-4, 0}, {3, 0}}], Line[{{0, -3}, {0, 4}}],
{Blue, Line[plastic]},
Style[Text[1, Mean[Take[plastic, 2]] - {0, .3}], 14],
Style[Text["\[Rho]", Mean[Take[plastic, -2]] + {.3, 0}], 14],
Text[#, # + {0, .2}] & /@ {p1, p2},
Red, Point[{p1, p2}], Green, Point /@ newpoints}]](https://www.wolframcloud.com/obj/resourcesystem/images/e81/e81b2484-9131-4fff-afc1-6494c9dfcf02/3c1014fad58f20ad.png) |
| Out[13]= | 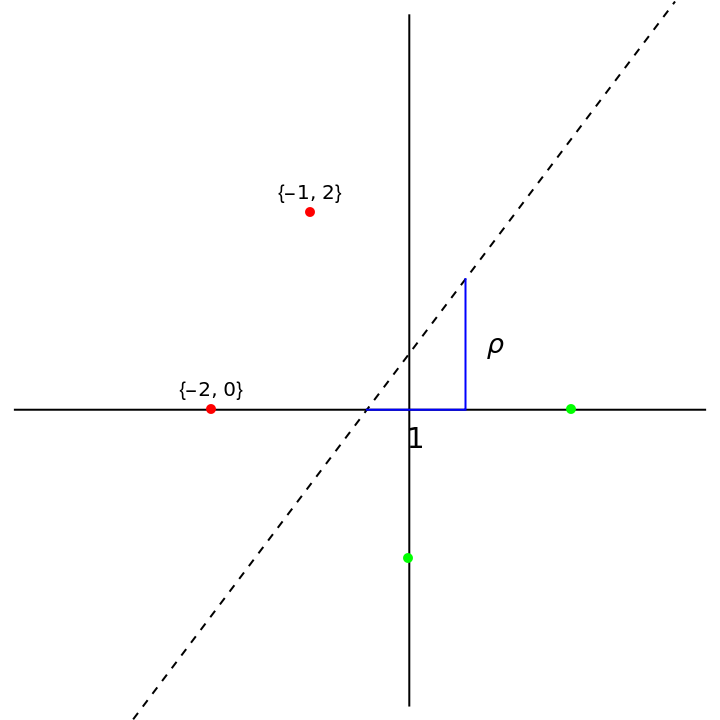 |
Fold two points to two arbitrary lines:
| In[14]:= | ![{p1, p2} = {{-2, 1}, {-1, 2}};
{l1, l2} := {{{-1, 0}, {0, 1}}, {{0, 2}, {2, 0}}};
folds = ResourceFunction["BelochFold"][{p1, l1}, {p2, l2}] // RootReduce](https://www.wolframcloud.com/obj/resourcesystem/images/e81/e81b2484-9131-4fff-afc1-6494c9dfcf02/6f314a01d4977ed0.png) |
| Out[15]= |
Show the fold:
| In[16]:= | ![newpoints = ResourceFunction["ReflectPoints"][#, {p1, p2}] & /@ folds;
Graphics[{ {Black, Dashed, InfiniteLine@# & /@ folds,
Cyan, InfiniteLine@# & /@ {l1, l2}},
AbsolutePointSize[5], EdgeForm[Black],
Line[{{-4, 0}, {3, 0}}], Line[{{0, -3}, {0, 4}}],
Text[#, # + {0, .2}] & /@ {p1, p2},
Red, Point[{p1, p2}], Green, Point /@ newpoints}]](https://www.wolframcloud.com/obj/resourcesystem/images/e81/e81b2484-9131-4fff-afc1-6494c9dfcf02/3f0d9c6933e23924.png) |
| Out[17]= | 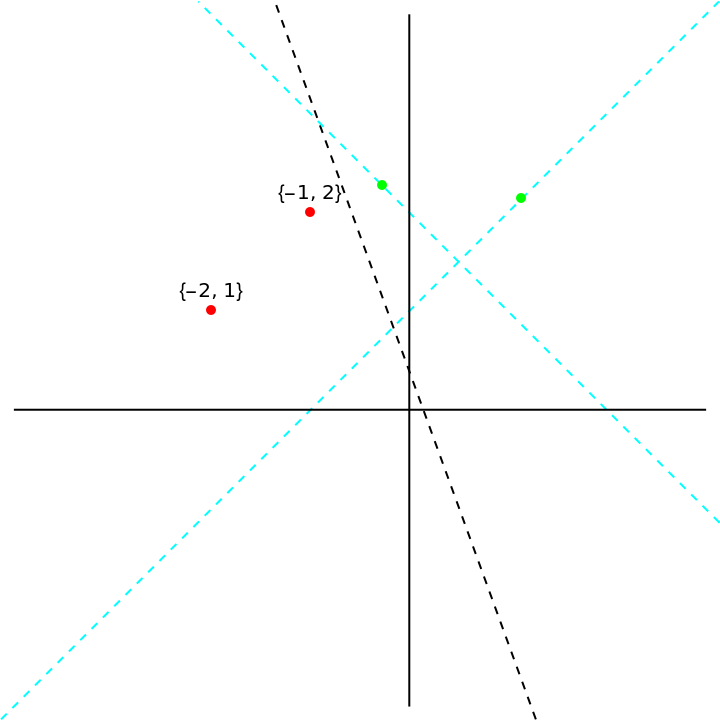 |
Find the folds that map two given points to the y and x axes:
| In[18]:= | ![{p1, p2} = {{-1, -1/2}, {0, 1}};
{yaxis, xaxis} := {{{0, 0}, {0, 1}}, {{0, 0}, {1, 0}}};
folds = ResourceFunction["BelochFold"][{p1, yaxis}, {p2, xaxis}] // RootReduce](https://www.wolframcloud.com/obj/resourcesystem/images/e81/e81b2484-9131-4fff-afc1-6494c9dfcf02/1dde190dac8bb477.png) |
| Out[20]= |
Show the starting origami step for folding a regular heptagon:
| In[21]:= | ![newpoints = ResourceFunction["ReflectPoints"][#, {p1, p2}] & /@ folds;
moveheptagon = ((# - CirclePoints[7][[1]] + folds[[3, 1]]) & /@ CirclePoints[7]) // RootReduce; Graphics[{ {Black, Dashed, InfiniteLine@# & /@ {folds[[3]]}
},
AbsolutePointSize[5], EdgeForm[Black],
Line[{{-4, 0}, {3, 0}}], Line[{{0, -3}, {0, 4}}],
Line[moveheptagon],
Text[#, # + {0, .2}] & /@ {p1, p2},
Red, Point[{p1, p2}], Green, Point /@ {newpoints[[3]]}}]](https://www.wolframcloud.com/obj/resourcesystem/images/e81/e81b2484-9131-4fff-afc1-6494c9dfcf02/2d12a708a2a5cb9f.png) |
| Out[22]= | 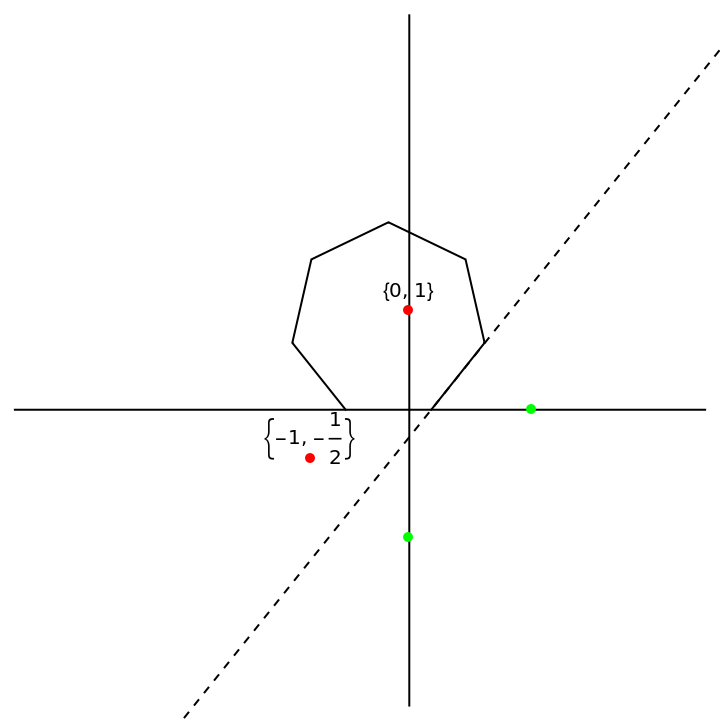 |
Wolfram Language 14.0 (January 2024) or above
This work is licensed under a Creative Commons Attribution 4.0 International License