Wolfram Function Repository
Instant-use add-on functions for the Wolfram Language
Function Repository Resource:
Find a cubic plane curve that passes through nine given 2D points
ResourceFunction["NinePointCubic"][pts,{x,y}] returns the implicit Cartesian equation in the variables x and y of the cubic plane curve that goes through the points pts. | |
ResourceFunction["NinePointCubic"][pts] uses the formal variables x and y. |
Find a cubic plane curve through nine points:
| In[1]:= | ![BlockRandom[SeedRandom[1];
p9 = RandomSample[Tuples[Range[-2, 2], {2}], 9]];
cubic = ResourceFunction["NinePointCubic"][p9, {x, y}]](https://www.wolframcloud.com/obj/resourcesystem/images/e64/e64a692d-8584-4643-9d9d-3d9cd5383f64/7173b45c27db8882.png) |
| Out[2]= |
Show the cubic and points:
| In[3]:= |
| Out[3]= | 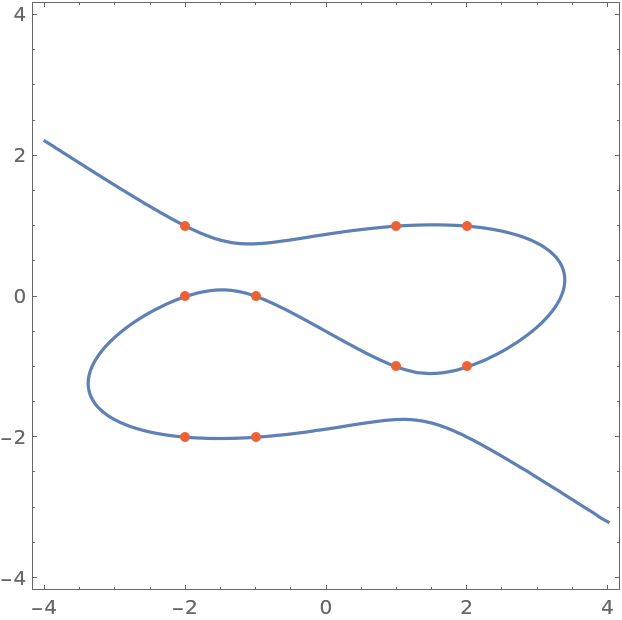 |
Find a cubic equation through nine points:
| In[4]:= | ![BlockRandom[SeedRandom[3];
p9 = RandomSample[Tuples[Range[-2, 2], {2}], 9]];
cubic = ResourceFunction["NinePointCubic"][p9, {x, y}]](https://www.wolframcloud.com/obj/resourcesystem/images/e64/e64a692d-8584-4643-9d9d-3d9cd5383f64/2c90a8ac7a56f96d.png) |
| Out[5]= |
Show the cubic and points:
| In[6]:= |
| Out[6]= | 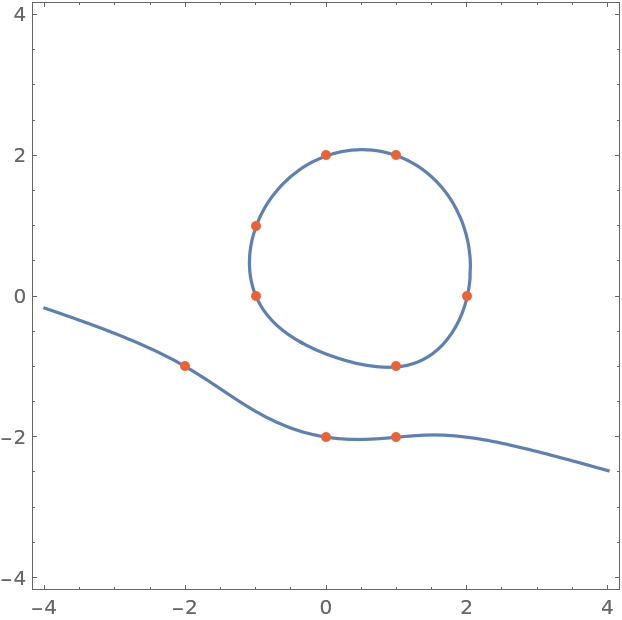 |
Use formal variables:
| In[7]:= |
| Out[7]= |
Find a cubic through nine points:
| In[8]:= |
| Out[9]= |
The cubic is factorizable and thus degenerate, and is composed of an ellipse and a line:
| In[10]:= |
| Out[10]= | 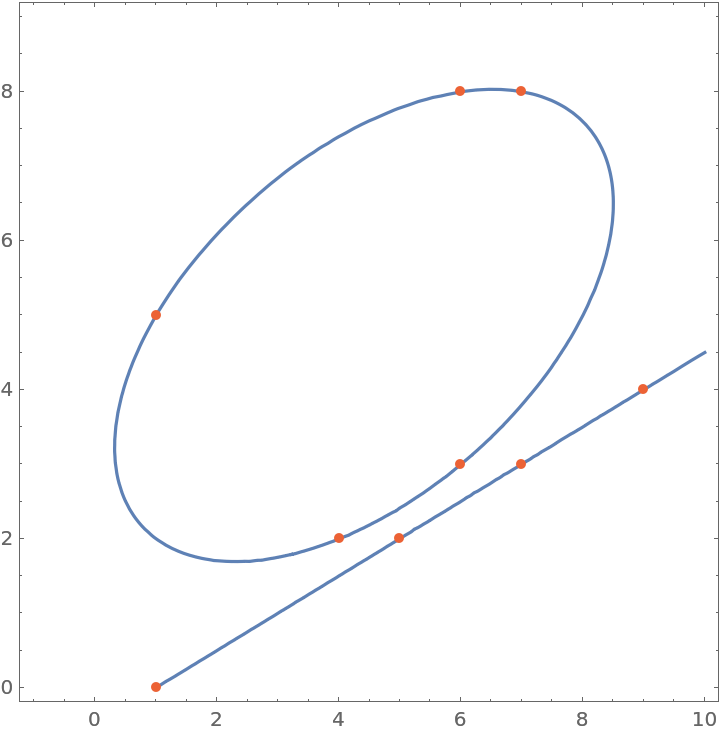 |
Some points and a cubic curve:
| In[11]:= |
| Out[12]= |
Any line going through two points of a cubic will meet one of three criteria: 1. it will go through a third point (gray), 2. it will be tangent at one of the points (red), or 3. it will be parallel with the cubics' asymptote (green), also called a point at infinity:
| In[13]:= | ![lines = ResourceFunction["FindExtraordinaryLines"][points];
linesinf = {{2, 10}, {3, 11}, {4, 8}, {5, 9}};
curve = ContourPlot[cubic == 0, {x, -9, 9}, {y, -9, 9}, ContourStyle -> Thickness[.02]][[1]];
ordinary = {{2, 5}, {3, 4}, {4, 9}, {4, 10}, {5, 8}, {5, 11}};
Graphics[{curve, EdgeForm[Thick], Gray, Line[points[[#]]] & /@ lines, Thick,
Green, InfiniteLine[points[[#]]] & /@ linesinf,
Red, InfiniteLine[points[[#]]] & /@ ordinary,
{White, Disk[#, .2]} & /@ points}]](https://www.wolframcloud.com/obj/resourcesystem/images/e64/e64a692d-8584-4643-9d9d-3d9cd5383f64/7e1fde7867fdaaa8.png) |
| Out[17]= | 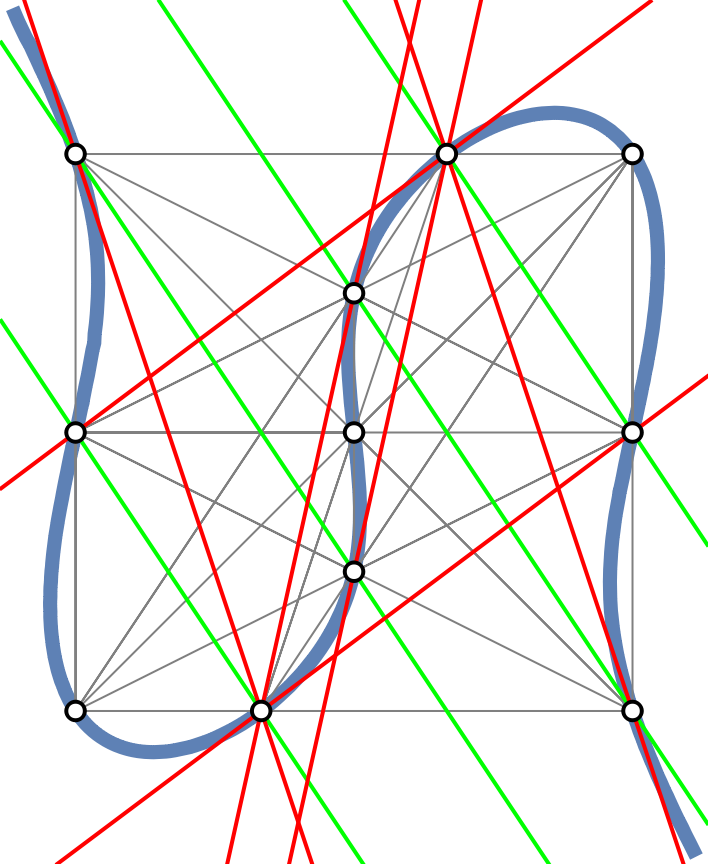 |
This work is licensed under a Creative Commons Attribution 4.0 International License