Wolfram Function Repository
Instant-use add-on functions for the Wolfram Language
Function Repository Resource:
Create a polygon from a list of midpoints
ResourceFunction["ReverseMidpointPolygon"][mid] returns a polygon or polyline with given midpoints mid. |
Find the vertices of a reverse midpoint polygon (rvp) for a given list of midpoints:
| In[1]:= | ![p = Round[50 (CirclePoints[7] + .01)];
rvp = ResourceFunction["ReverseMidpointPolygon"][p]](https://www.wolframcloud.com/obj/resourcesystem/images/e5e/e5e349a1-b3ef-4954-baef-ae20d4e64cff/4f33df8ad7cfafe1.png) |
| Out[2]= |
Check that the midpoints of rvp match the given list of midpoints:
| In[3]:= |
| Out[3]= |
Show both:
| In[4]:= |
| Out[4]= |  |
Repeat a few more times:
| In[5]:= | ![Graphics[{Opacity[.5], EdgeForm[Black], White, Polygon /@ Reverse[NestList[ResourceFunction["ReverseMidpointPolygon"][#] &, p, 3]]}]](https://www.wolframcloud.com/obj/resourcesystem/images/e5e/e5e349a1-b3ef-4954-baef-ae20d4e64cff/350d2dba48cffcca.png) |
| Out[5]= | 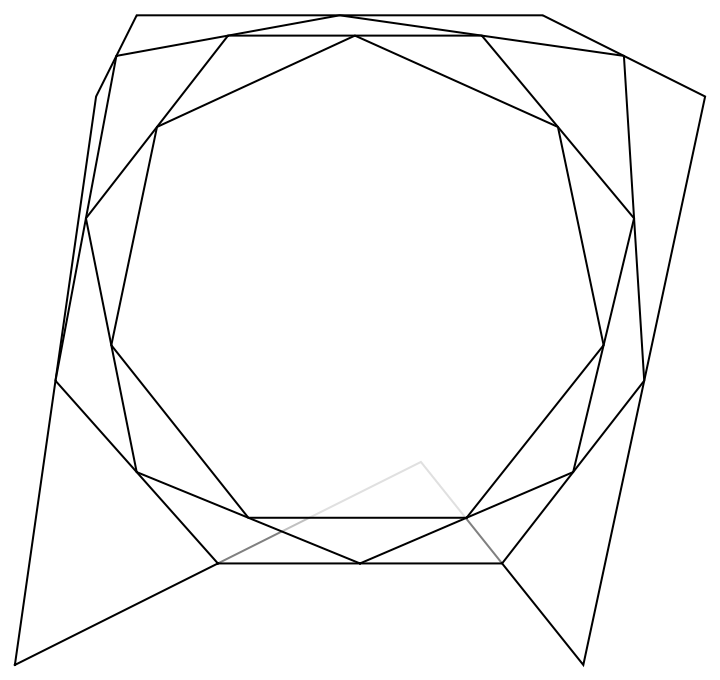 |
For a square, find one of the many reverse midpoint polygons:
| In[6]:= |
| Out[7]= |
Show it:
| In[8]:= |
| Out[8]= | 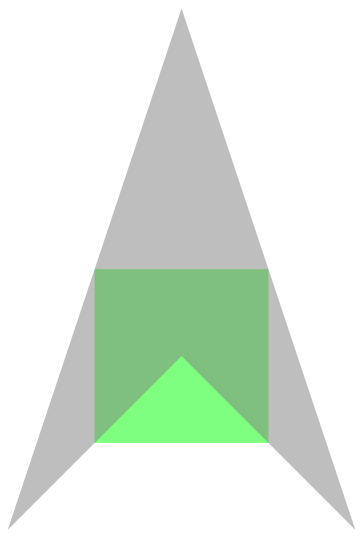 |
Try a skew quadrilateral:
| In[9]:= |
| Out[10]= |
One of many possible polylines is returned with the given midpoints. For any solution, the ends of the polyline are separated by a vector four times the magnitude of the vector between diagonal midpoints:
| In[11]:= | ![Graphics[{Opacity[.5], Green, Polygon[p], Black, Line[r], Blue, Line[p[[{1, 3}]]], Line[p[[{2, 4}]]], Thick, Red, Line[{Mean[p[[{1, 3}]]], Mean[p[[{2, 4}]]]}]}]](https://www.wolframcloud.com/obj/resourcesystem/images/e5e/e5e349a1-b3ef-4954-baef-ae20d4e64cff/79824a5ecd0c1cc3.png) |
| Out[11]= |  |
Find one of the many solutions for the regular hexagon:
| In[12]:= | ![Graphics[{Opacity[.5], Green, Polygon[CirclePoints[6]], Gray, Polygon[ResourceFunction["ReverseMidpointPolygon"][
CirclePoints[6]]]}]](https://www.wolframcloud.com/obj/resourcesystem/images/e5e/e5e349a1-b3ef-4954-baef-ae20d4e64cff/74e534c27b1d5b6b.png) |
| Out[12]= |  |
Find one of many polylines with a given set of six midpoints:
| In[13]:= | ![p = Round[10 Drop[CirclePoints[7], 1]];
r = ResourceFunction["ReverseMidpointPolygon"][p]](https://www.wolframcloud.com/obj/resourcesystem/images/e5e/e5e349a1-b3ef-4954-baef-ae20d4e64cff/4679340a5817d008.png) |
| Out[14]= |
Check that the polyline ends have 6 times the separation of the even and odd centroids:
| In[15]:= |
| Out[15]= |
Show the polyline with the displacement between the even and odd centroids:
| In[16]:= | ![Graphics[{Opacity[.5], Green, Polygon[p], Black, Line[r], Thick, Red, Line[{Mean[p[[{1, 3, 5}]]], Mean[p[[{2, 4, 6}]]]}]}]](https://www.wolframcloud.com/obj/resourcesystem/images/e5e/e5e349a1-b3ef-4954-baef-ae20d4e64cff/1fa106edf8fa683f.png) |
| Out[16]= |  |
Find a Varignon-balanced extension for a pentagon:
| In[17]:= |
| Out[17]= |
| In[18]:= |
| Out[18]= |
Find the ReverseMidpointPolygon:
| In[19]:= |
| Out[20]= |
Show it:
| In[21]:= |
| Out[21]= |  |
If an even number of points is even slightly unbalanced, a polyline is returned instead:
| In[22]:= |
| Out[23]= |
Find a polygon with midpoints on an octagon:
| In[24]:= | ![p = Round[10 Drop[CirclePoints[9], 1]];
r = ResourceFunction["ReverseMidpointPolygon"][p]](https://www.wolframcloud.com/obj/resourcesystem/images/e5e/e5e349a1-b3ef-4954-baef-ae20d4e64cff/7b0e548f1cd1bbc3.png) |
| Out[25]= |
Check that the polyline ends have 8 times the separation of the even and odd centroids:
| In[26]:= |
| Out[26]= |
Show the polyline with the displacement between the even and odd centroids:
| In[27]:= | ![Graphics[{Opacity[.5], Green, Polygon[p], Black, Line[r], Thick, Red, Line[{Mean[p[[{1, 3, 5, 7}]]], Mean[p[[{2, 4, 6, 8}]]]}]}]](https://www.wolframcloud.com/obj/resourcesystem/images/e5e/e5e349a1-b3ef-4954-baef-ae20d4e64cff/4263a62edabd9262.png) |
| Out[27]= |  |
Wolfram Language 14.0 (January 2024) or above
This work is licensed under a Creative Commons Attribution 4.0 International License