Wolfram Function Repository

Instant-use add-on functions for the Wolfram Language

Function Repository Resource:

 RamanujanPrimes

Source Notebook

Compute Ramanujan primes

Contributed by: Shenghui Yang

ResourceFunction["RamanujanPrimes"][n]

returns the first n Ramanujan primes.

Details

The n-th Ramanujan prime is the smallest number Rn such that π(x)-π(x/2)>=n for all x>=Rn, where π(x) is the prime counting function.
RamanujanPrimes uses FunctionCompile to accelerate the speed of computation.This function may take some time for initial evaluation due to compilation, but subsequent evaluation is faster than the non-compiled implementation in the same session.
Effectively use Sieve of Eratosthenes to build a "BitVector" data structure as a prime number lookup table.

Examples

Basic Examples (1) 

Compute the first twenty Ramanujan primes:

In[1]:=
ResourceFunction["RamanujanPrimes"][20]
Out[1]=

Scope (4) 

It takes only around 9 seconds to find the all Ramanujan primes less than 109 on modern computers:

In[2]:=
rp = NumericArray[ResourceFunction["RamanujanPrimes"][24491666], "Integer32"]; // AbsoluteTiming
Out[2]=

The largest Ramanujan prime just under 109:

In[3]:=
rp[[-1]]
Out[3]=

The number of Ramanujan primes less than one billion:

In[4]:=
Length[rp]
Out[4]=

Compute the same number using the definition of Ramanujan primes:

In[5]:=
PrimePi[rp[[-1]]] - PrimePi[rp[[-1]]/2]
Out[5]=

Properties and Relations (3) 

Recover the sequence of natural numbers from Ramanujan primes:

In[6]:=
rp = ResourceFunction["RamanujanPrimes"][20]
Out[6]=
In[7]:=
PrimePi[#] - PrimePi[#/2] & /@ rp
Out[7]=

For all n>=1, we have the following bounds for the n-th Ramanujan prime:

In[8]:=
rp = ResourceFunction["RamanujanPrimes"][200];
In[9]:=
DiscretePlot[{2*n*Log[2*n], rp[[n]], 41/47*Prime[3*n]}, {n, 200}, Filling -> None, PlotLegends -> {2*n*Log[2*n], "nth Ramanujan Prime", Row[{41/47, Prime[3 n]}]}]
Out[9]=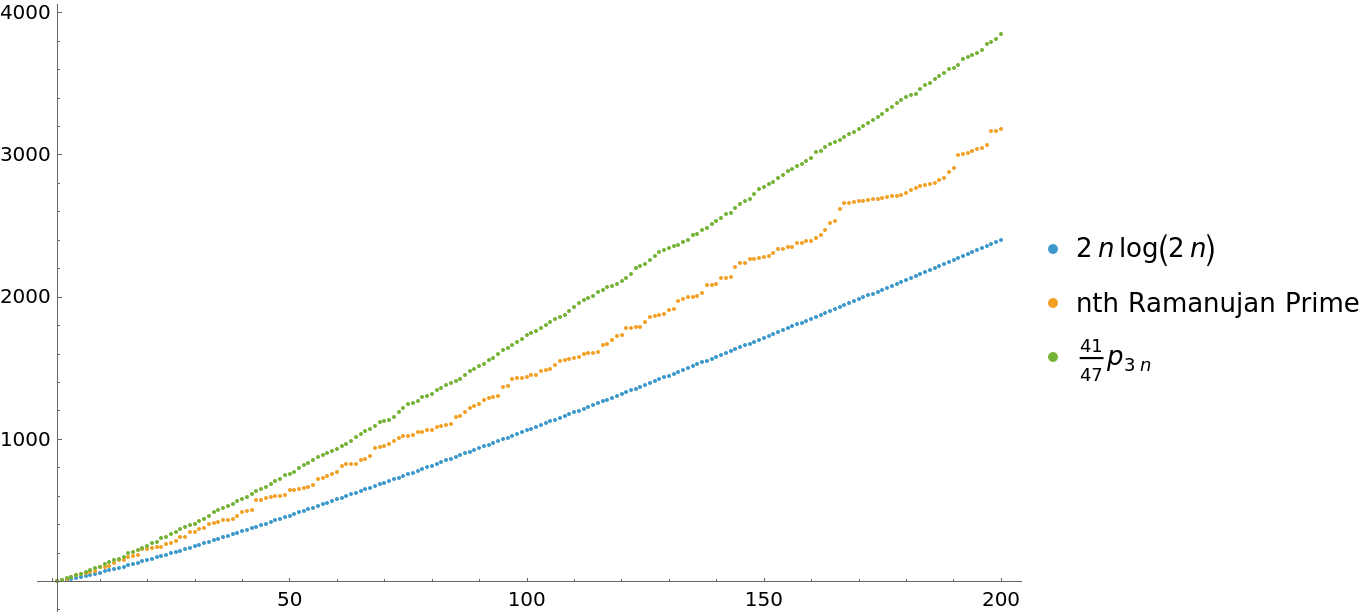

Use "Ramanujan Primes" on Wolfram Demonstrations to visualize the patterns for small Ramanujan primes:

In[10]:=
ResourceData["Demonstration: Ramanujan Primes"]
Out[10]=

Possible Issues (1) 

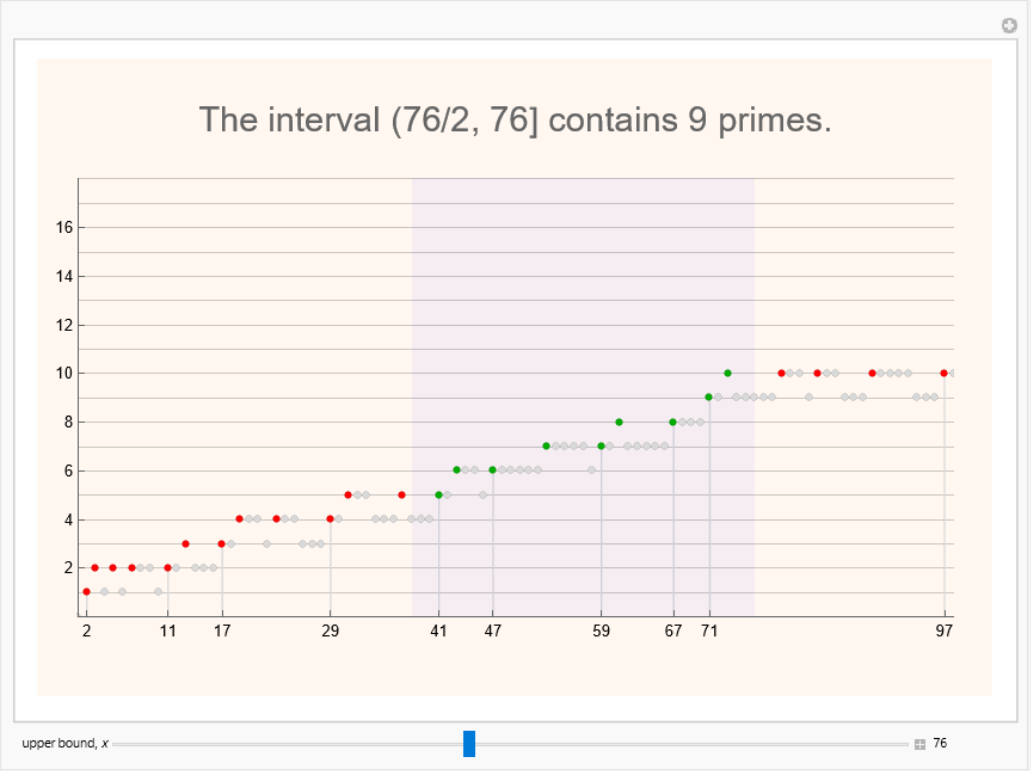The input must be positive integer. Otherwise it returns unevaluated:

In[11]:=
ResourceFunction["RamanujanPrimes"][-10]
Out[11]=

Neat Examples (2) 

If pn+2 = pn+1, then pn and pn+1 are twin primes. If Rn+2 = Rn+1, then Rn and Rn+1 are twin Ramanujan primes; the smallest are 149 and 151. Find the number twin Ramanujan primes in the first 100k Ramanujan primes:

In[12]:=
rp = ResourceFunction["RamanujanPrimes"][10^6];
In[13]:=
gap = Differences@rp;

The distribution of gaps between Ramanujan primes:

In[14]:=
Histogram[gap, {1}, Ticks -> {{ 2, Splice[Range[20, 100, 20]]}, Automatic}]
Out[14]=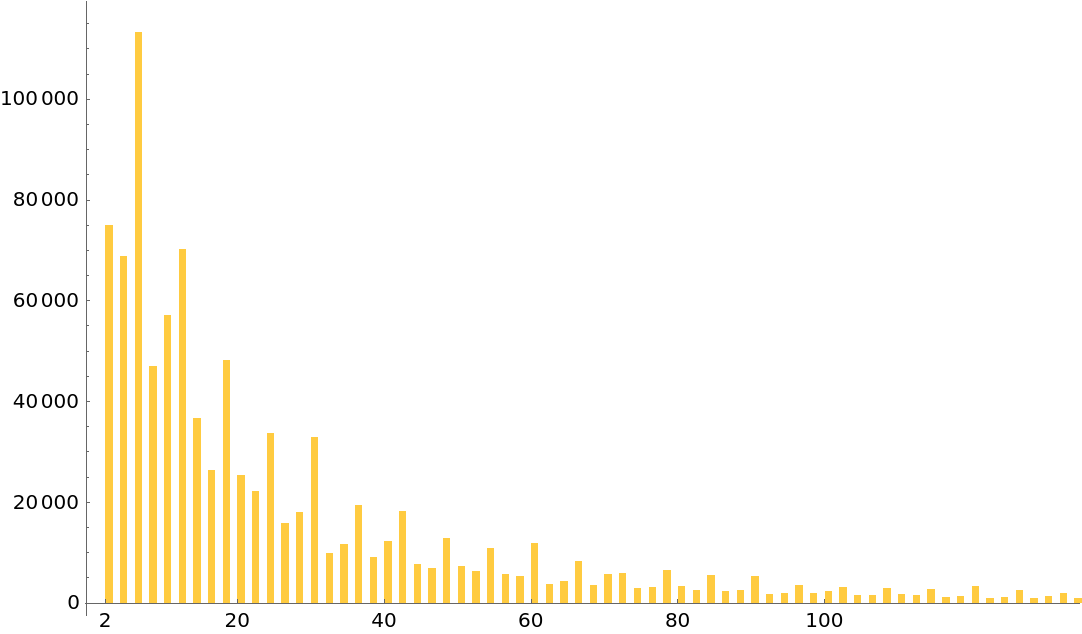

The number of pairs of twin Ramanujan primes:

In[15]:=
Count[gap, 2]
Out[15]=

See the twin Ramanujan primes:

In[16]:=
Short[trp = rp[[{#, # + 1}]] & /@ Flatten[Position[gap, 2]], 3]
Out[16]=

Import a definition of Brun's constant. This is an analogous topic:

In[17]:=
Style[Entity["MathWorld", "BrunsConstant"][ EntityProperty["MathWorld", "TypesetDescription"]], FontFamily -> "Helvetica"]
Out[17]=

Here only twin Ramanujan primes are applied:

In[18]:=
Total[1/N[Flatten[trp], 50]]
Out[18]=

The number of twin Ramanujan prime pairs less than 10, 100, 1000,…, 109:

In[19]:=
res = ResourceFunction["RamanujanPrimes"][24491666]; loc = ResourceFunction["BinarySearch"][res, #] & /@ (10^Range[3, 9]); ct = Count[Differences[res[[;; # - 1]]], 2] & /@ loc;
In[20]:=
ResourceFunction["NiceGrid"][ Transpose@{Range[3, 9], ct}, {"\!\(\*SuperscriptBox[\(10\), \(n\)]\)", "# of Twin RP"}, Alignment -> Right]
Out[20]=

Publisher

Shenghui Yang

Requirements

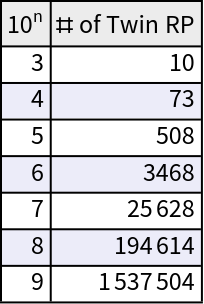Wolfram Language 14.0 (January 2024) or above

Version History

  • 1.0.0 – 22 January 2025

Source Metadata

  • Citation:
    • Sondow, Jonathan. Ramanujan Prime. From MathWorld--A Wolfram Web Resource, created by Eric W. Weisstein.
    • J. Sondow, J.W. Nicholson, T. D. Noe. "Ramanujan Primes: Bounds, Runs, Twins, and Gaps", Journal of Integer Sequences, Vol. 14 (2011), Article 11.6.2
    • Weisstein, Eric W. Twin Prime Conjecture. From MathWorld--A Wolfram Web Resource.

Related Resources

License Information