Wolfram Function Repository

Instant-use add-on functions for the Wolfram Language

Function Repository Resource:

 DedekindPsi

Source Notebook

Evaluate the Dedekind psi function

Contributed by: Long Yat Chan

ResourceFunction["DedekindPsi"][n]

gives the Dedekind psi function ψ(n).

ResourceFunction["DedekindPsi"][k,n]

gives the generalized Dedekind psi function ψk(n).

Details

Integer mathematical function, suitable for both symbolic and numerical manipulation.
ResourceFunction["DedekindPsi"][1] and ResourceFunction["DedekindPsi"][k,1] both equal 1.
For n≥2 with prime factorization , ResourceFunction["DedekindPsi"][n] gives .
For n≥2 with prime factorization , ResourceFunction["DedekindPsi"][k,n] gives .
ResourceFunction["DedekindPsi"] automatically threads over lists.

Examples

Basic Examples (3) 

Evaluate ψ(3):

In[1]:=
ResourceFunction["DedekindPsi"][3]
Out[1]=

Evaluate ψ(2,8):

In[2]:=
ResourceFunction["DedekindPsi"][2, 8]
Out[2]=

Plot ψ(k,n) for several values of k on a logarithmic scale:

In[3]:=
(* Evaluate this cell to get the example input *) CloudGet["https://www.wolframcloud.com/obj/26b000ae-825f-45b7-b449-a871ebf45cdf"]
Out[3]=

Scope (4) 

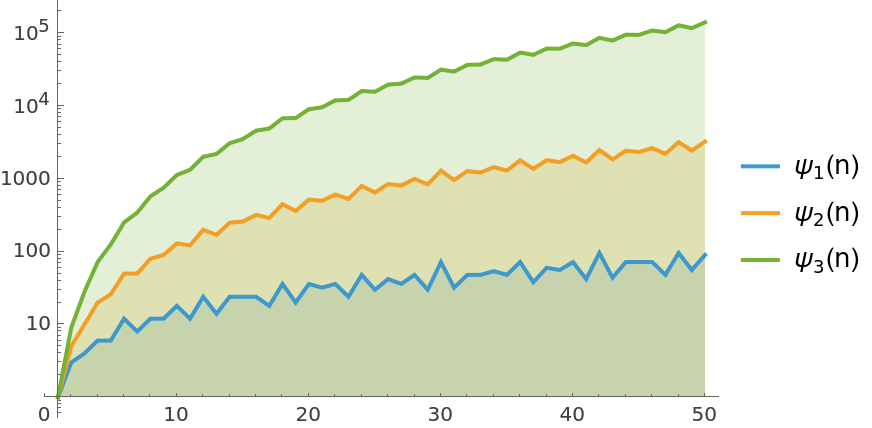DedekindPsi threads elementwise over lists for either argument:

In[4]:=
ResourceFunction["DedekindPsi"][{2, 4, 6, 8, 10}]
Out[4]=
In[5]:=
ResourceFunction["DedekindPsi"][2, {2, 3, 4}]
Out[5]=
In[6]:=
ResourceFunction["DedekindPsi"][{1, 2, 3, 4}, 12]
Out[6]=

Obtain a symbolic expression for arbitrary order k:

In[7]:=
ResourceFunction["DedekindPsi"][k, 52]
Out[7]=
In[8]:=
{% /. k -> 4, ResourceFunction["DedekindPsi"][4, 52]}
Out[8]=

DedekindPsi[k,n] remains unevaluated for symbolic n:

In[9]:=
ResourceFunction["DedekindPsi"][5, n]
Out[9]=

Now specify a value:

In[10]:=
% /. n -> 4
Out[10]=

The Dirichlet transform of DedekindPsi can be expressed in terms of Zeta:

In[11]:=
DirichletTransform[ResourceFunction["DedekindPsi"][k, n], n, s]
Out[11]=

Applications (1) 

The average order of DedekindPsi[n] is :

In[12]:=
Show[{DiscretePlot[ResourceFunction["DedekindPsi"][n], {n, 50}, Joined -> True, PlotLegends -> {"\[Psi](n)"}, ScalingFunctions -> "Log"], Plot[Log[15 n/(Pi^2)], {n, 1, 50}, PlotLegends -> {"\!\(\*FormBox[FractionBox[\(15\\\ n\), SuperscriptBox[\(\[Pi]\), \(2\)]], TraditionalForm]\)"}, PlotStyle -> Orange, Filling -> 0]}]
Out[12]=

Properties and Relations (5) 

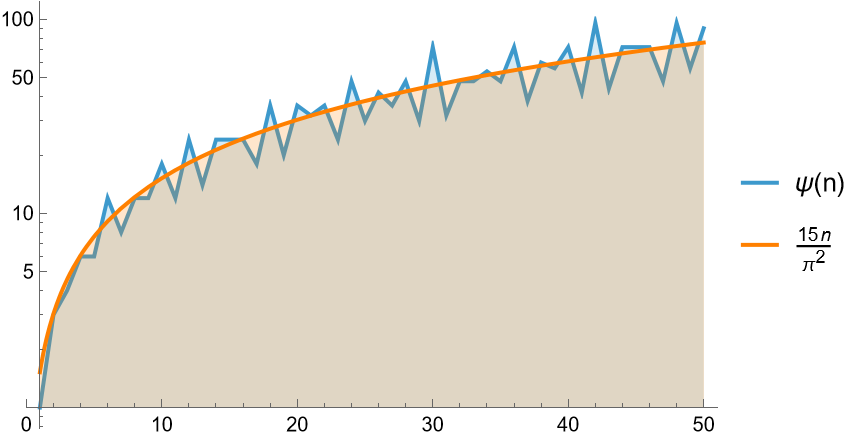DedekindPsi[k,n] can be expressed as a quotient of Jordan’s generalized totients :

In[13]:=
ResourceFunction["DedekindPsi"][3, Range[10]]
Out[13]=
In[14]:=
ResourceFunction["JordanTotient"][2*3, Range[10]]/ ResourceFunction["JordanTotient"][3, Range[10]]
Out[14]=

DedekindPsi[k,n] is a multiplicative function:

In[15]:=
ResourceFunction["DedekindPsi"][2, 3]* ResourceFunction["DedekindPsi"][2, 10]
Out[15]=
In[16]:=
ResourceFunction["DedekindPsi"][2, 3*10]
Out[16]=
In[17]:=
CoprimeQ[3, 10]
Out[17]=

If n is squarefree, DedekindPsi[k,n] = DivisorSigma[k,n]:

In[18]:=
{ResourceFunction["DedekindPsi"][345], DivisorSigma[1, 345]}
Out[18]=
In[19]:=
{ResourceFunction["DedekindPsi"][3, 345], DivisorSigma[3, 345]}
Out[19]=
In[20]:=
SquareFreeQ[345]
Out[20]=

When the order is zero, all terms in the defining product degenerate to 2, i.e. DedekindPsi[0,n] degenerates to 2^PrimeNu[n]:

In[21]:=
ResourceFunction["DedekindPsi"][0, 3465]
Out[21]=
In[22]:=
2^PrimeNu[3465]
Out[22]=

DedekindPsi[k,n] can be expressed as μ(n)2⋆nk where ⋆ is DirichletConvolve:

In[23]:=
ResourceFunction["DedekindPsi"][2, 14]
Out[23]=
In[24]:=
psi[k_, n_] := DirichletConvolve[MoebiusMu[m]^2, m^k, m, n]; psi[2, 14]
Out[25]=

However, for large n, this calculation is slower:

In[26]:=
bigN = Prime[10^10] Prime[2*10^10] Prime[5*10^8]; {RepeatedTiming[ResourceFunction["DedekindPsi"][2, bigN]], RepeatedTiming[psi[2, bigN]]}
Out[27]=

Possible Issues (1) 

DedekindPsi[0] is undefined:

In[28]:=
ResourceFunction["DedekindPsi"][0]
Out[28]=

Neat Examples (2) 

Plot the Ulam spiral where numbers are colored based on the values of DedekindPsi:

In[29]:=
ulam[n_] := Partition[ Permute[Range[n^2], Accumulate[ Take[Flatten[{{n^2 + 1}/2, Table[(-1)^j i, {j, n}, {i, {-1, n}}, {j}]}], n^2]]], n]; ArrayPlot[ResourceFunction["DedekindPsi"][ulam[71]], ColorFunction -> Hue]
Out[30]=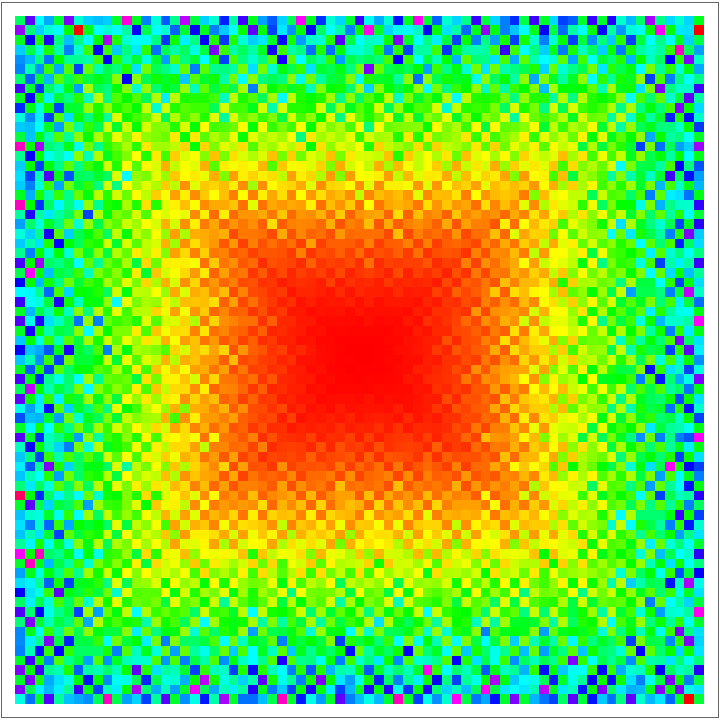

Verify that small Mersenne primes p satisfy ψ(2(ψ(n)−n)-1)=n where n=p+1:

In[31]:=
mersennePrimesPlusOne = 2^Table[MersennePrimeExponent[n], {n, 15}]
Out[31]=
In[32]:=
Function[n, ResourceFunction["DedekindPsi"][ 2 (ResourceFunction["DedekindPsi"][n] - n) - 1] == n] /@ mersennePrimesPlusOne
Out[32]=

Publisher

Clintmok-Imha Ifolyfin

Requirements

Wolfram Language 13.0 (December 2021) or above

Version History

  • 1.0.0 – 01 August 2025

Related Resources

Author Notes

Motivated by JordanTotient whose formula is a simple sign change.

License Information