Wolfram Function Repository
Instant-use add-on functions for the Wolfram Language
Function Repository Resource:
Visualize the Earth's umbra and penumbra in the sky
ResourceFunction["LunarEclipseStarChart"][] generates a star chart showing the current position of the Earth's umbra and penumbra. | |
ResourceFunction["LunarEclipseStarChart"][date] generates a star chart showing the position of the Earth's umbra and penumbra on the specified date. |
| "AdditionalElements" | {} | additional graphical elements to include |
| AstroGridLines | Quantity[1,"AngularDegrees"] | coordinate grid lines to draw |
| AstroProjection | "Stereographic" | projection to use |
| AstroRange | Quantity[2,"AngularDegrees"] | area of the sky to include |
| AstroReferenceFrame | {"Equatorial", date} | observation data (frame, date, location, …) |
| "PenumbraStyle" | Directive[Orange,EdgeForm[Gray],Opacity[.15]] | style to use for the penumbra |
| "ShadowEnlargementFactor" | 1.01 | shadow enlargement factor |
| "UmbraStyle" | Directive[Red,EdgeForm[Gray],Opacity[.15]] | style to use for the umbra |
Plot the penumbra and umbra against the current sky:
| In[1]:= |
| Out[1]= |  |
Plot the penumbra and umbra against the sky for the lunar eclipse on March 14, 2025:
| In[2]:= |
| Out[2]= | 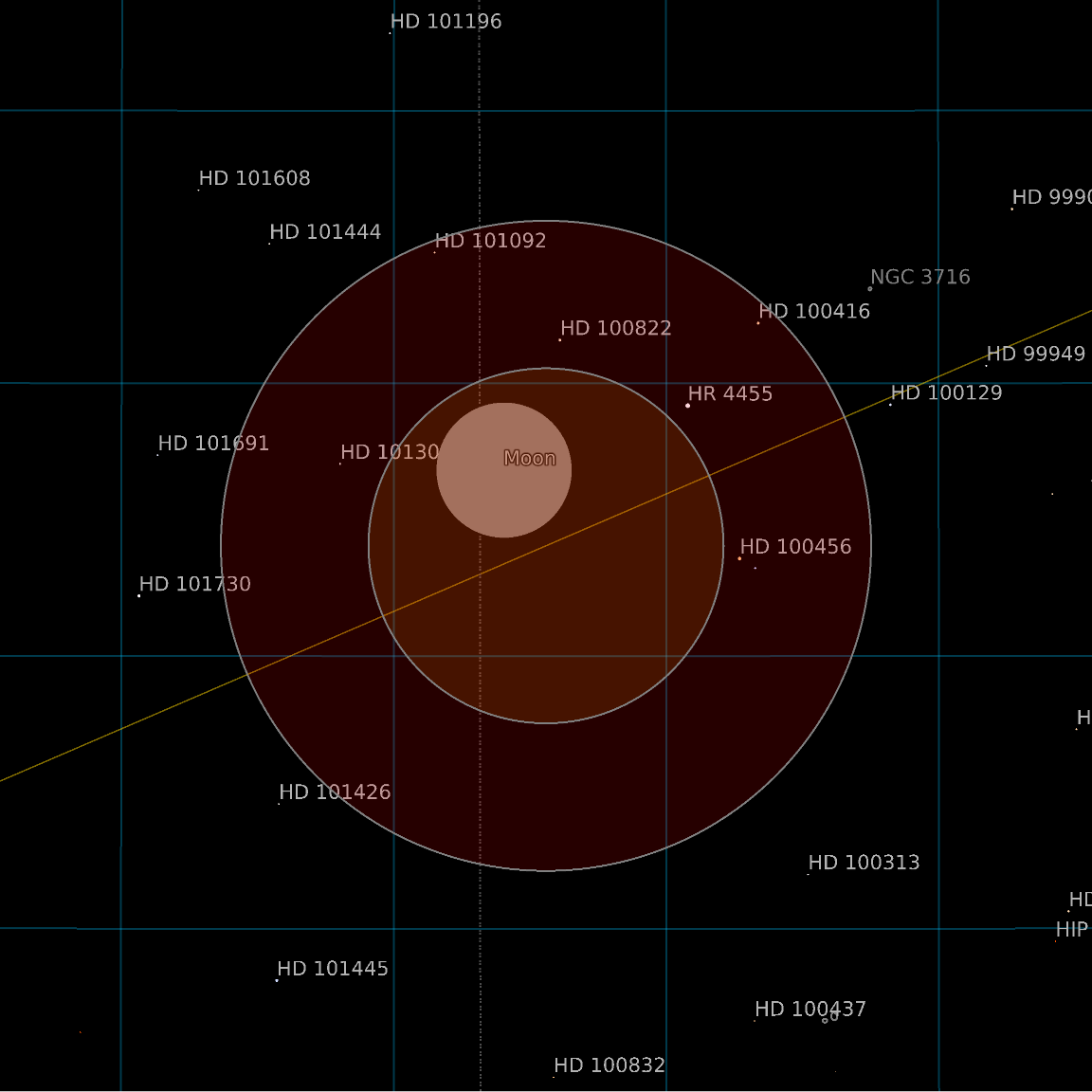 |
Partial lunar eclipses begin when the Moon just touches the umbra:
| In[3]:= |
| Out[3]= |  |
Partial lunar eclipses end when the Moon just touches the umbra:
| In[4]:= |
| Out[4]= | 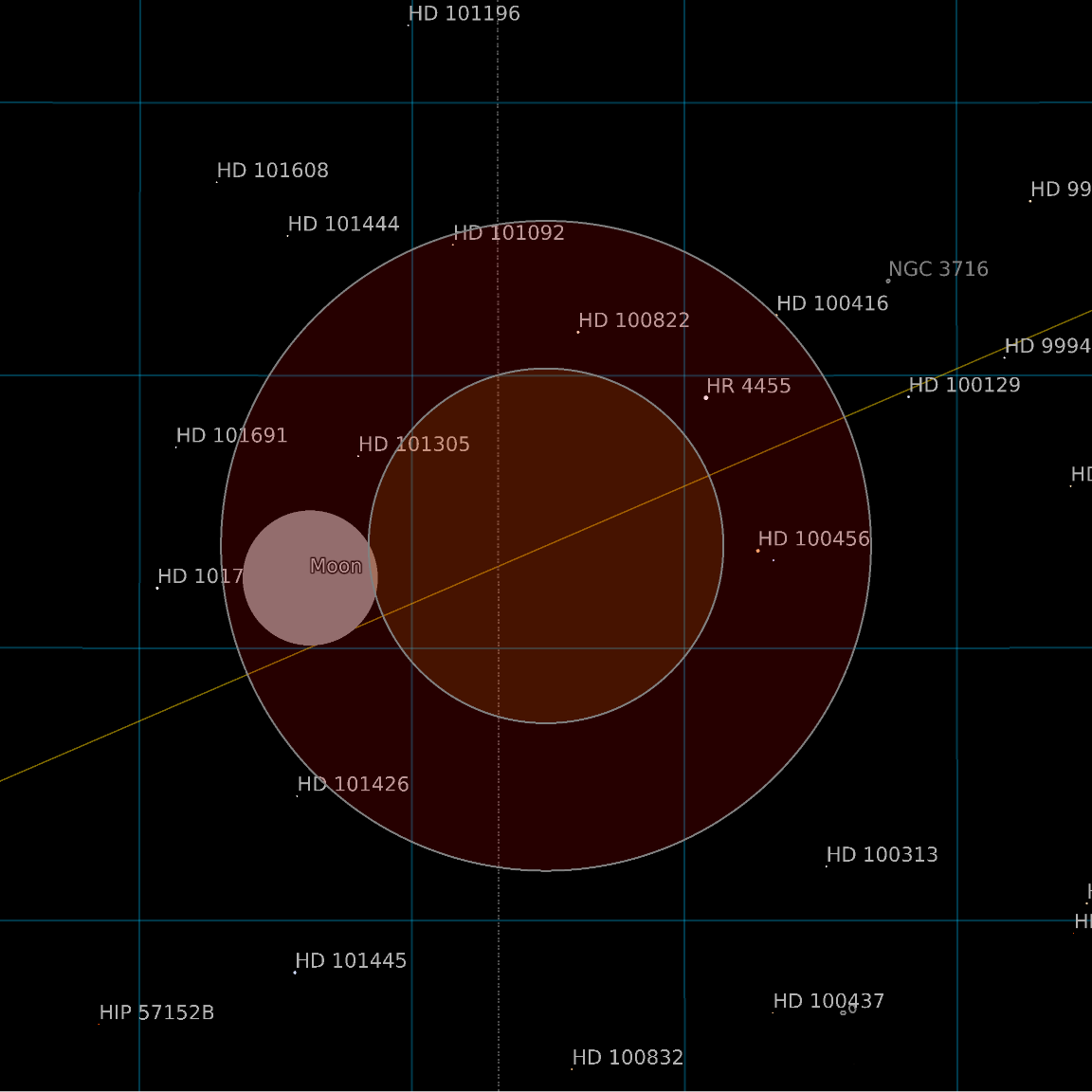 |
Lunar eclipses start the total phase when the entire Moon enters the umbra:
| In[5]:= |
| Out[5]= | 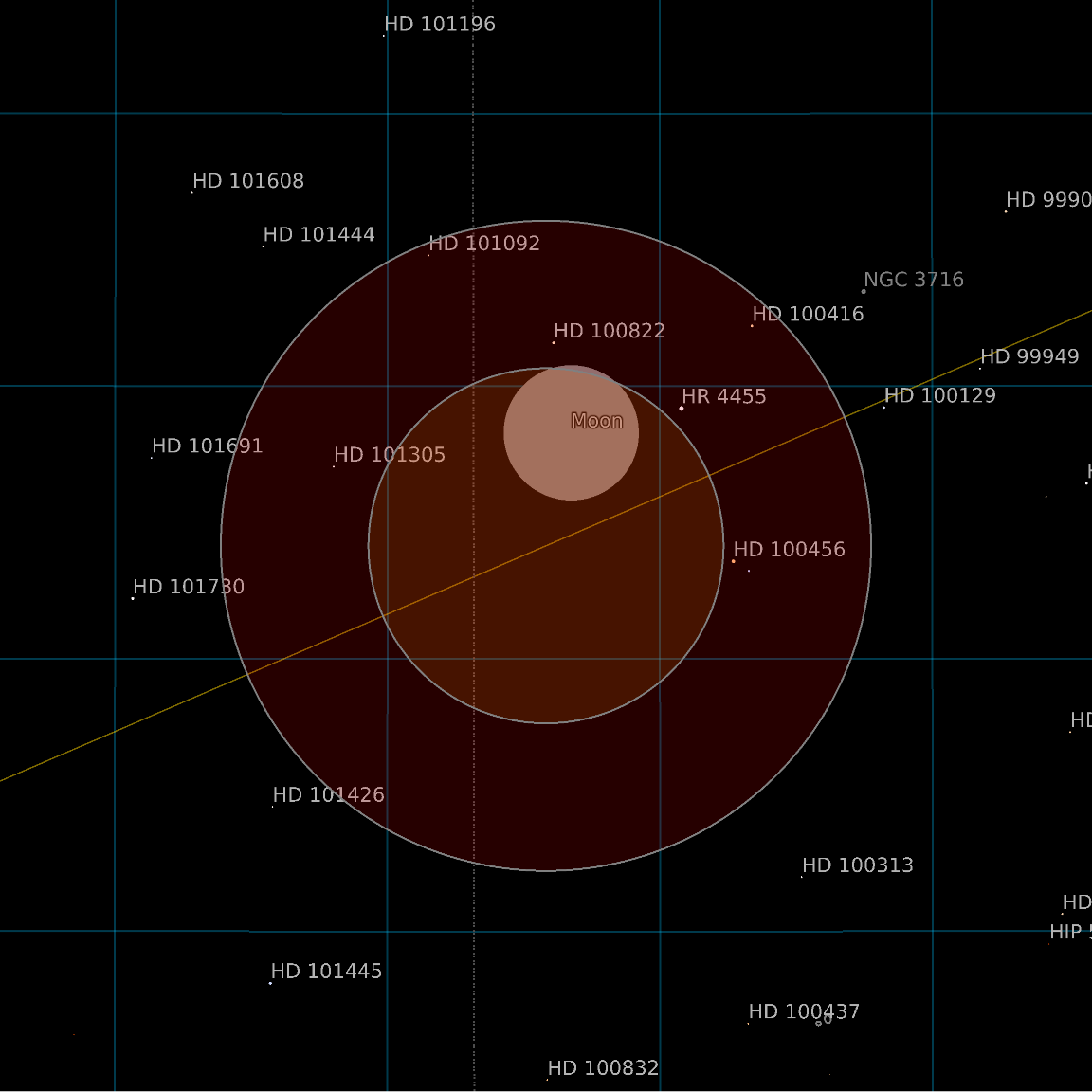 |
Lunar eclipses end the total phase when the Moon starts to exit the umbra:
| In[6]:= |
| Out[6]= | 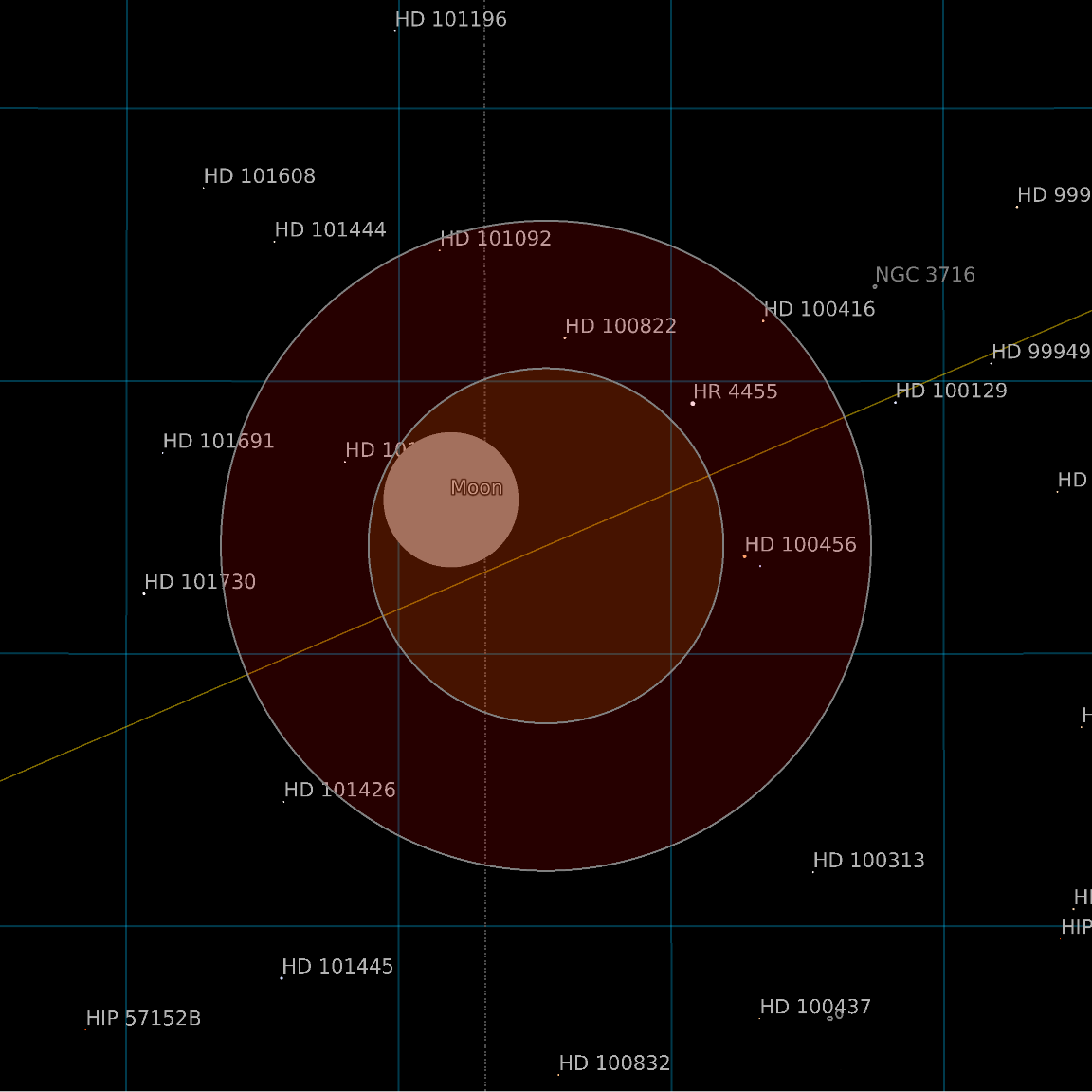 |
Add any additional graphics primitives, such as text, as additional elements to the scene:
| In[7]:= |
| Out[7]= |
| In[8]:= | ![ResourceFunction["LunarEclipseStarChart"][eclipse, "AdditionalElements" -> {Text[
Style[DateString[eclipse] <> " GMT", White, 14], ImageScaled[{.5, .9}]]}]](https://www.wolframcloud.com/obj/resourcesystem/images/e3b/e3baa959-2920-4623-9b56-d76b09578200/6caebdb3870f6100.png) |
| Out[8]= | 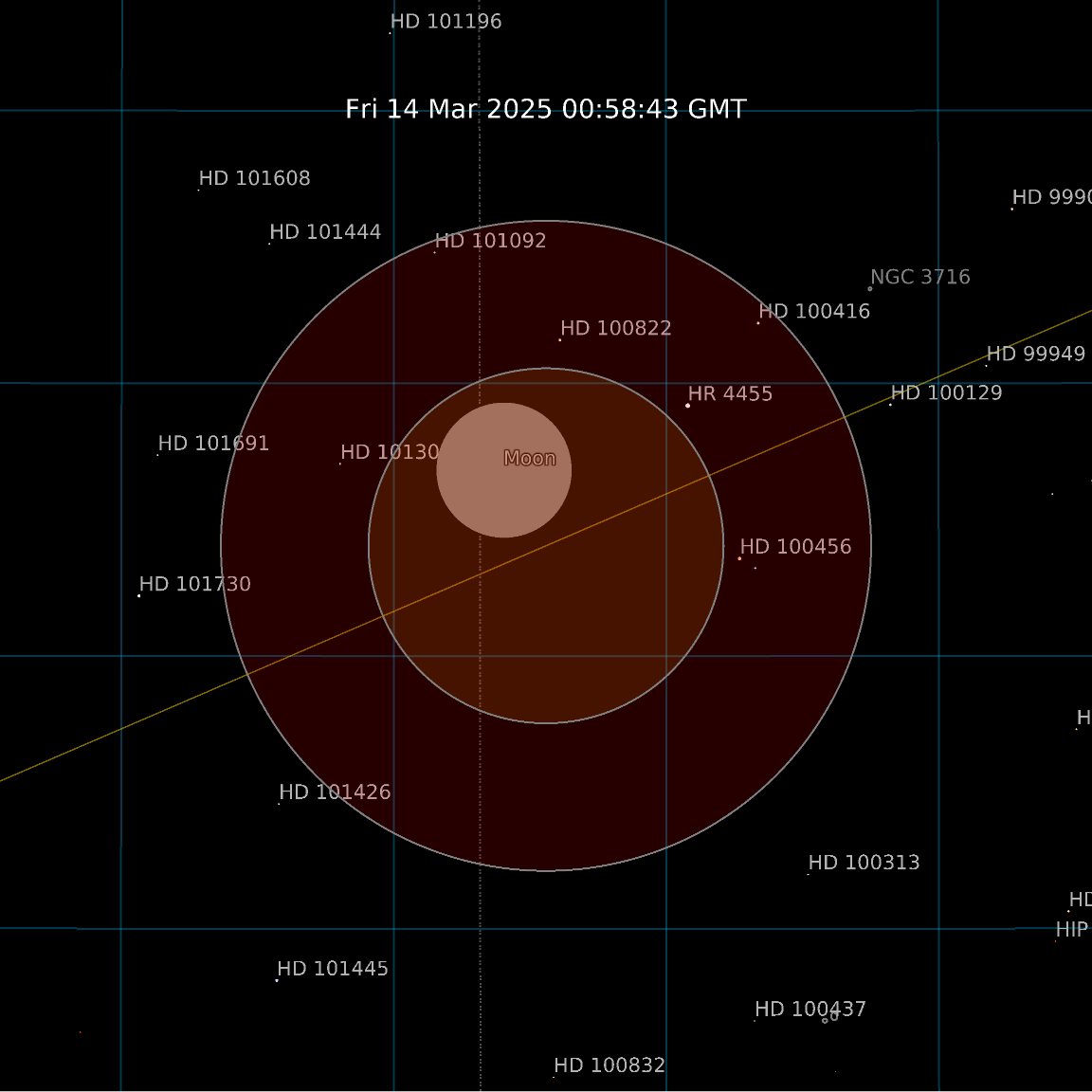 |
Retrieve the dates of various phases of an eclipse:
| In[9]:= |
| In[10]:= |
| In[11]:= |
| In[12]:= |
| In[13]:= |
Compute the angular radius of the Moon for the eclipse date:
| In[14]:= | ![moonRadiusRadians = QuantityMagnitude[
Entity["PlanetaryMoon", "Moon"][
Dated["AngularRadiusFromEarth", eclipseMax]], "Radians"];](https://www.wolframcloud.com/obj/resourcesystem/images/e3b/e3baa959-2920-4623-9b56-d76b09578200/4b8337a5f405068d.png) |
Draw white circles showing the position of the Moon at each date and time:
| In[15]:= | ![ResourceFunction["LunarEclipseStarChart"][eclipse, AstroBackground -> AstroStyling[{"BlackSky", "ShowSolarSystemObjects" -> False}], "AdditionalElements" -> {White,
Circle[AstroPosition["Moon", eclipsePartialStart], moonRadiusRadians],
Circle[AstroPosition["Moon", eclipseStart], moonRadiusRadians], Circle[AstroPosition["Moon", eclipseMax], moonRadiusRadians], Circle[AstroPosition["Moon", eclipseEnd], moonRadiusRadians],
Circle[AstroPosition["Moon", eclipsePartialEnd], moonRadiusRadians]}]](https://www.wolframcloud.com/obj/resourcesystem/images/e3b/e3baa959-2920-4623-9b56-d76b09578200/4a1ed46ec83cd6e6.png) |
| Out[15]= |  |
Change the style of the penumbra disk:
| In[16]:= |
| Out[16]= |  |
Change the style of the umbra disk:
| In[17]:= |
| Out[17]= |  |
Due to unpredictable atmospheric effects, a scaling factor is applied to the apparent radius of the Earth's shadow:
| In[18]:= |
| Out[18]= | 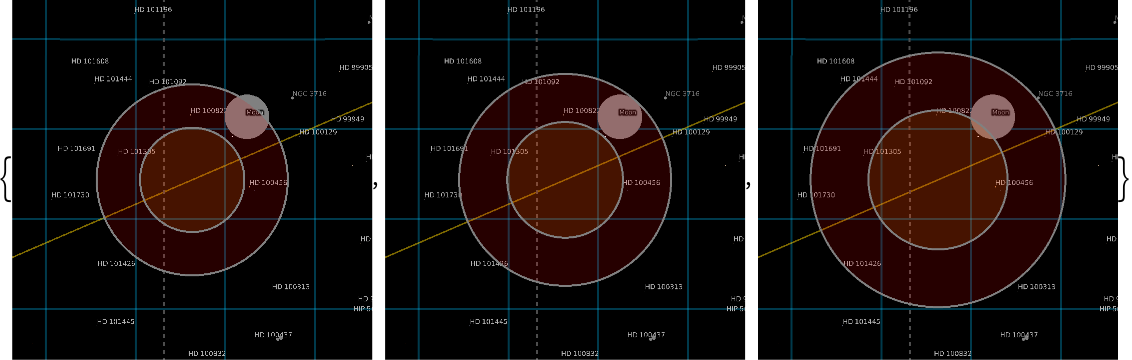 |
LunarEclipse timings are not as precise as SolarEclipse so contact points may not be exact:
| In[19]:= |
| Out[19]= |  |
Manually putting in the expected time (as found at https://www.timeanddate.com/eclipse/lunar/2025-march-14) provides better results:
| In[20]:= |
| Out[20]= |  |
Wolfram Language 14.0 (January 2024) or above
This work is licensed under a Creative Commons Attribution 4.0 International License