Function Repository Resource:

Immanant

Source Notebook

Compute the immanant of a square matrix associated with an integer partition

Contributed by: Jan Mangaldan

ResourceFunction["Immanant"][p,m]

gives the immanant of the square matrix m associated with the integer partition p.

Details

ResourceFunction["Immanant"] works with both numeric and symbolic matrices.

The immanant of an n×n matrix m associated with the integer partition p is given by

, where χ^(p)(σ) is the character of the symmetric group corresponding to p and the P_n are the permutations of n elements.

The immanant is a generalization of the determinant and the permanent of a square matrix.

If m has dimensions n×n, then p must be a weakly decreasing list of positive integers that sum to n.

The immanant is a polynomial of degree n in its entries.

Examples

Basic Examples (1)

Immanants of a 2×2 symbolic matrix:

In[1]:=

$ResourceFunction["Immanant"][{1, 1}, \!$\* TagBox[ RowBox[{"(", "", GridBox[{ { SubscriptBox["a", RowBox[{"1", ",", "1"}]], SubscriptBox["a", RowBox[{"1", ",", "2"}]]}, { SubscriptBox["a", RowBox[{"2", ",", "1"}]], SubscriptBox["a", RowBox[{"2", ",", "2"}]]} }, GridBoxAlignment->{"Columns" -> {{Left}}, "ColumnsIndexed" -> {}, "Rows" -> {{Baseline}}, "RowsIndexed" -> {}}, GridBoxSpacings->{"Columns" -> { Offset[ 0.27999999999999997`], { Offset[0.7]}, Offset[0.27999999999999997`]}, "ColumnsIndexed" -> {}, "Rows" -> { Offset[0.2], { Offset[0.4]}, Offset[0.2]}, "RowsIndexed" -> {}}], "", ")"}], Function[BoxForm`e$, MatrixForm[BoxForm`e$]]]$]$

Out[1]=

In[2]:=

$ResourceFunction["Immanant"][{2}, \!$\* TagBox[ RowBox[{"(", "", GridBox[{ { SubscriptBox["a", RowBox[{"1", ",", "1"}]], SubscriptBox["a", RowBox[{"1", ",", "2"}]]}, { SubscriptBox["a", RowBox[{"2", ",", "1"}]], SubscriptBox["a", RowBox[{"2", ",", "2"}]]} }, GridBoxAlignment->{"Columns" -> {{Left}}, "ColumnsIndexed" -> {}, "Rows" -> {{Baseline}}, "RowsIndexed" -> {}}, GridBoxSpacings->{"Columns" -> { Offset[ 0.27999999999999997`], { Offset[0.7]}, Offset[0.27999999999999997`]}, "ColumnsIndexed" -> {}, "Rows" -> { Offset[0.2], { Offset[0.4]}, Offset[0.2]}, "RowsIndexed" -> {}}], "", ")"}], Function[BoxForm`e$, MatrixForm[BoxForm`e$]]]$]$

Out[2]=

Scope (2)

All immanants of a 3×3 symbolic matrix:

In[3]:=

$ResourceFunction["Immanant"][#, \!$\* TagBox[ RowBox[{"(", "", GridBox[{ { SubscriptBox["a", RowBox[{"1", ",", "1"}]], SubscriptBox["a", RowBox[{"1", ",", "2"}]], SubscriptBox["a", RowBox[{"1", ",", "3"}]]}, { SubscriptBox["a", RowBox[{"2", ",", "1"}]], SubscriptBox["a", RowBox[{"2", ",", "2"}]], SubscriptBox["a", RowBox[{"2", ",", "3"}]]}, { SubscriptBox["a", RowBox[{"3", ",", "1"}]], SubscriptBox["a", RowBox[{"3", ",", "2"}]], SubscriptBox["a", RowBox[{"3", ",", "3"}]]} }, GridBoxAlignment->{"Columns" -> {{Left}}, "ColumnsIndexed" -> {}, "Rows" -> {{Baseline}}, "RowsIndexed" -> {}}, GridBoxSpacings->{"Columns" -> { Offset[ 0.27999999999999997`], { Offset[0.7]}, Offset[0.27999999999999997`]}, "ColumnsIndexed" -> {}, "Rows" -> { Offset[0.2], { Offset[0.4]}, Offset[0.2]}, "RowsIndexed" -> {}}], "", ")"}], Function[BoxForm`e$, MatrixForm[BoxForm`e$]]]$] & /@ IntegerPartitions[3]$

Out[3]=

Use exact arithmetic to compute the immanant:

In[4]:=

In[5]:=

Out[5]=

Use machine arithmetic:

In[6]:=

Out[6]=

Use 24-digit precision arithmetic:

In[7]:=

Out[7]=

Applications (3)

Two graphs:

In[8]:=

Out[8]=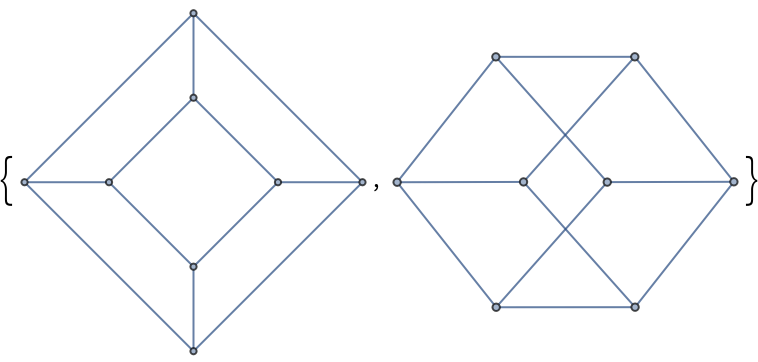

The immanantal polynomial of a graph is the immanant of id x-m, where m is the corresponding adjacency matrix and id is the identity matrix of appropriate size.

Prove that two graphs are isomorphic by showing that all their corresponding immanantal polynomials are identical:

In[9]:=

n = VertexCount[g];
mg = AdjacencyMatrix[g];
mh = AdjacencyMatrix[h];

In[10]:=

Out[10]=

This is consistent with the result of IsomorphicGraphQ:

In[11]:=

Out[11]=

Properties and Relations (3)

The determinant is the immanant corresponding to the integer partition (1,1,…):

In[12]:=

Out[13]=

The permanent is the immanant corresponding to the integer partition (n):

In[14]:=

Out[15]=

Immanants are invariant under a symmetric permutation of rows and columns:

In[16]:=

n = 5;
m = Array[C, {n, n}];
{partition, permutation} = {RandomChoice[IntegerPartitions[n]], RandomSample[Range[n]]}

Out[18]=

In[19]:=

Out[19]=

Possible Issues (2)

Immanant evaluates only if the integer partition p is a weakly decreasing list of positive integers:

In[20]:=

In[21]:=

Out[21]=

In[22]:=

Out[22]=

In general, computing the immanant becomes slow even at modest dimension:

In[23]:=

Out[23]=

In[24]:=

Out[24]=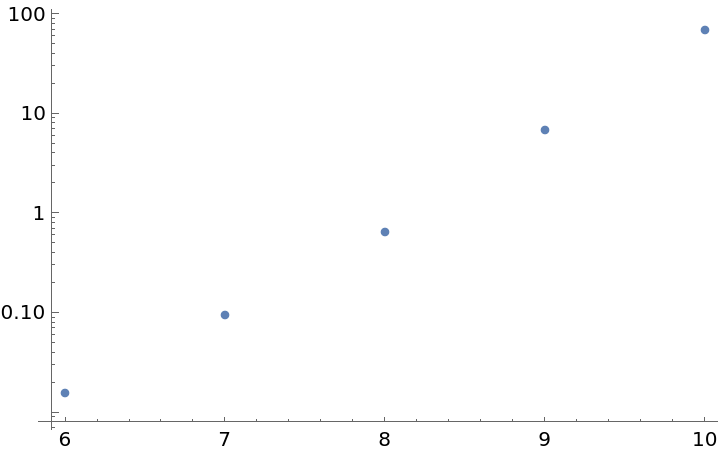

Neat Examples (1)

Verify an identity for the immanant corresponding to the partition (3, 1, 1, …) according to Merris and Watkins (see citation in Source Metadata below):

In[25]:=

Out[26]=

In[27]:=

$ResourceFunction["Immanant"][part, mat] == \!$ \*UnderoverscriptBox[\(\[Sum]$, $i = 1$, $n$]$ \*UnderoverscriptBox[\(\[Sum]$, $j = 1$, $n$]Boole[ 1 <= i < j <= n] Permanent[ mat[$[$${i, j}, {i, j}$$]$]] Det[ Map[Delete[#, {{i}, {j}}] &, mat, {0, 1}]]\)\) - \!$ \*UnderoverscriptBox[\(\[Sum]$, $i = 1$, $n$]$mat[\([$$i, i$$]$] Det[Drop[mat, {i}, {i}]]\)\) + Det[mat] // Expand$

Out[27]=

Version History

1.0.0 – 24 January 2022

Source Metadata

Citation:
- Hartmann, W., "On the complexity of immanants." Linear and Multilinear Algebra, vol. 18, no. 2, 127–140, 1985. DOI: 10.1080/03081088508817680
- Merris R., Watkins W., "Inequalities and identities for generalized matrix functions." Linear Algebra and its Applications, vol. 64, 223–242, 1985. DOI: 10.1016/0024-3795(85)90279-4

Related Resources

Author Notes

Parts of the implementation are adapted from the GroupMath package by Renato Fonseca.

License Information

This work is licensed under a Creative Commons Attribution 4.0 International License

Wolfram Function Repository

Immanant

Details