Wolfram Function Repository
Instant-use add-on functions for the Wolfram Language
Function Repository Resource:
Get the three mixtilinear incircles of a triangle
ResourceFunction["MixtilinearIncircles"][{p1,p2,p3}] gives the three mixtilinear incircles for a triangle with vertices p1,p2 and p3. | |
ResourceFunction["MixtilinearIncircles"][{p1,p2,p3},property] returns additional related geometric objects of the mixtilinear incircles for the given property. | |
ResourceFunction["MixtilinearIncircles"][{p1,p2,p3},{prop1,…}] returns a list of properties. |
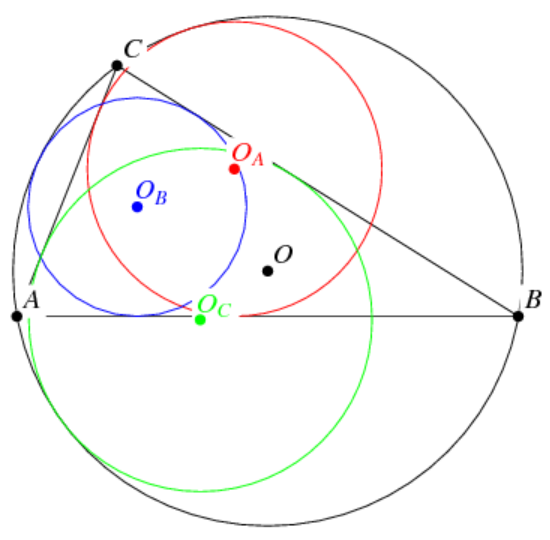
| "Circles" | the mixtilinear incircles of a triangle |
| "MixtilinearIncircles" | same as "Circles" |
| "MixtilinearIncenters" | the centers of mixtilinear incircles of a triangle |
| "MixtilinearInradii" | the radii of mixtilinear incircles of a triangle |
| "MixtilinearTriangle" | the triangle connecting the three mixtilinear incenters |
| "MixtilinearCircle" | the circumcircle of the mixtilinear triangle |
| "MixtilinearRadicalAxes" | the radical axes of pairs of the mixtilinear incircles |
| "MixtilinearRadicalCenter" | the intersection of the radical axes |
| "ContactsOnCirumcircle" | the contacts between mixtilinear incircles and circumcircle |
| "OverlappingInversions" | combination of circle inversion and reflection along the angle bisector |
| "X56" | the concurrence of lines joining vertices and contacts on the circumcircle |
| All | an association including all properties given above |
Find the three mixtilinear incircles for a reference triangle:
| In[1]:= |
| Out[1]= |
An equivalent specification:
| In[2]:= |
| Out[2]= |
Find a list of properties for a triangle:
| In[3]:= |
| Out[3]= |
Visualize the three mixtilinear circles along with the reference triangle:
| In[4]:= | ![tri = Triangle[{{0, 0}, {1.2, 4}, {5, 0.5}}];
Graphics[{
{Opacity[0.2], Orange, tri},
{Opacity[0.4], ResourceFunction["MixtilinearIncircles"][tri]},
{Dashed, TriangleConstruct[tri, "Circumcircle"]}
}] // Framed](https://www.wolframcloud.com/obj/resourcesystem/images/de6/de672aa0-29a5-4c72-a11f-2b2c05a82cd0/623478b1db1c3c81.png) |
| Out[4]= |  |
MixtilinearIncircles works with Triangle objects:
| In[5]:= |
| Out[5]= |
Find the mixtilinear incircles for several triangles:
| In[6]:= | ![triList = Triangle[{
{{0, 0}, {1.2, 4}, {5, 0.5}},
{{0.5, -0.5}, {1.2, 3}, {5, 0}}
}];
ResourceFunction["MixtilinearIncircles"][triList]](https://www.wolframcloud.com/obj/resourcesystem/images/de6/de672aa0-29a5-4c72-a11f-2b2c05a82cd0/69b009211e17e708.png) |
| Out[6]= |
In the leftmost diagram, the overlapping inversion for vertex A={0,0} uses circle inversion at A with power ![]() and then applies the reflection transformation about the angular bisector of A. This operation sends the mixtilinear incircle and circumcircle contact point (black) to the blue point, which is the contact point between A-excircle and side BC:
and then applies the reflection transformation about the angular bisector of A. This operation sends the mixtilinear incircle and circumcircle contact point (black) to the blue point, which is the contact point between A-excircle and side BC:
| In[7]:= |
| In[8]:= | ![(* Evaluate this cell to get the example input *) CloudGet["https://www.wolframcloud.com/obj/fdb3bc3e-7f28-4063-9f95-a7023cb6f158"]](https://www.wolframcloud.com/obj/resourcesystem/images/de6/de672aa0-29a5-4c72-a11f-2b2c05a82cd0/0c80f13e55076977.png) |
| Out[8]= | 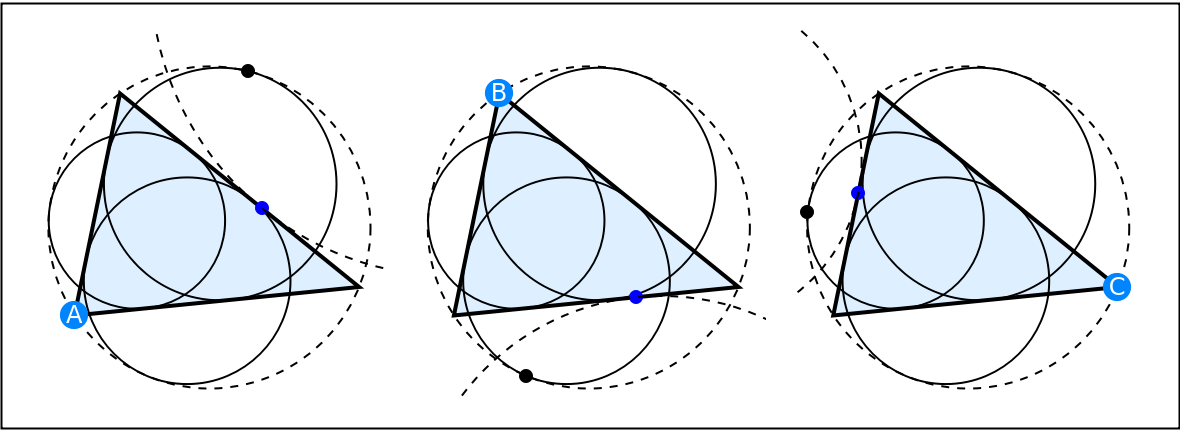 |
Therefore, the lines connecting A to the blue point and A to the black point are isogonal conjugate with respect to the angle bisector of A. Similar results apply to B and C.
The isogonal conjugacy also relates the Nagel point (brown) and the Kimberling center X56 (blue). The latter is the concurrence of the lines joining the vertex and the corresponding mixtilinear incircle-to-circumcircle contact point:
| In[9]:= | ![(* Evaluate this cell to get the example input *) CloudGet["https://www.wolframcloud.com/obj/64ad8262-ae16-4e3a-96f8-8c77c7cc9251"]](https://www.wolframcloud.com/obj/resourcesystem/images/de6/de672aa0-29a5-4c72-a11f-2b2c05a82cd0/07f75df10eee81e9.png) |
| Out[9]= | 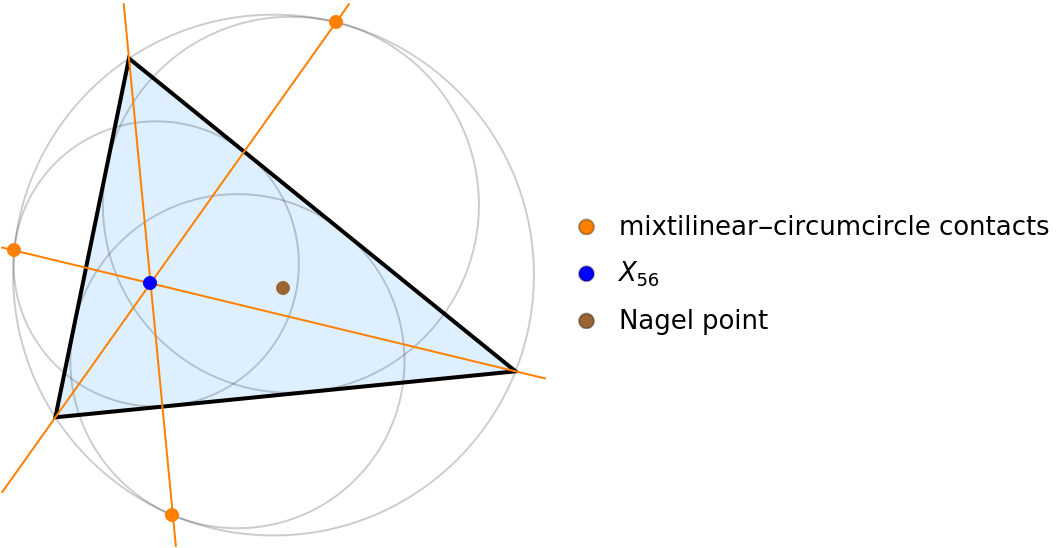 |
Given triangle ABC, the overlapping inversion at A sends the incenter to the A-excenter. Similar results apply to B and C:
| In[10]:= | ![tri = {{0, 0}, {0.8, 3.9}, {5, 0.5}};
{TriangleConstruct[tri, {"Excenter", tri[[1]]}],
ResourceFunction["MixtilinearIncircles"][tri, "OverlappingInversions"][[1]][TriangleConstruct[tri, "Incenter"]]}](https://www.wolframcloud.com/obj/resourcesystem/images/de6/de672aa0-29a5-4c72-a11f-2b2c05a82cd0/031b063e701749a8.png) |
| Out[10]= |
Display all available information from MixtilinearIncircles in a dataset:
| In[11]:= |
| Out[11]= |  |
For a given triangle, the point X56 (blue), mixtilinear radical center (red), incenter (orange) and circumcenter (black) are collinear:
| In[12]:= | ![tri = {{0, 0}, {0.8, 4}, {5, .5}};
circumCen = TriangleConstruct[tri, "Circumcenter"];
inCen = TriangleConstruct[tri, "Incenter"];
x56 = ResourceFunction["MixtilinearIncircles"][tri, "X56"];
mrc = ResourceFunction["MixtilinearIncircles"][tri, "MixtilinearRadicalCenter"];](https://www.wolframcloud.com/obj/resourcesystem/images/de6/de672aa0-29a5-4c72-a11f-2b2c05a82cd0/5361f4a03d2a6ef2.png) |
Show the collinearity:
| In[13]:= |
| Out[13]= |
| In[14]:= |
| Out[14]= |
Visualize the points and the line passing the four points:
| In[15]:= | ![Legended[Graphics[{
{LightBlue, EdgeForm[Thick], Triangle[tri]},
{Dashed, Opacity[0.5], InfiniteLine[{inCen[[1]], circumCen[[1]]}]},
{Opacity[0.2], TriangleConstruct[tri, "Circumcircle"], ResourceFunction["MixtilinearIncircles"][tri]},
PointSize[Large], {Blue, x56}, {Red, mrc}, {Orange, inCen}, {Black,
circumCen}
}],
PointLegend[{Blue, Red, Orange, Black}, {"\!\(\*SubscriptBox[\(X\), \(56\)]\)", "mixtilinear radical center", "incenter", "circumcenter"}, LegendMarkers -> ConstantArray[Graphics[Disk[]], 4]]]](https://www.wolframcloud.com/obj/resourcesystem/images/de6/de672aa0-29a5-4c72-a11f-2b2c05a82cd0/3277ee4ff80ee4b9.png) |
| Out[15]= | 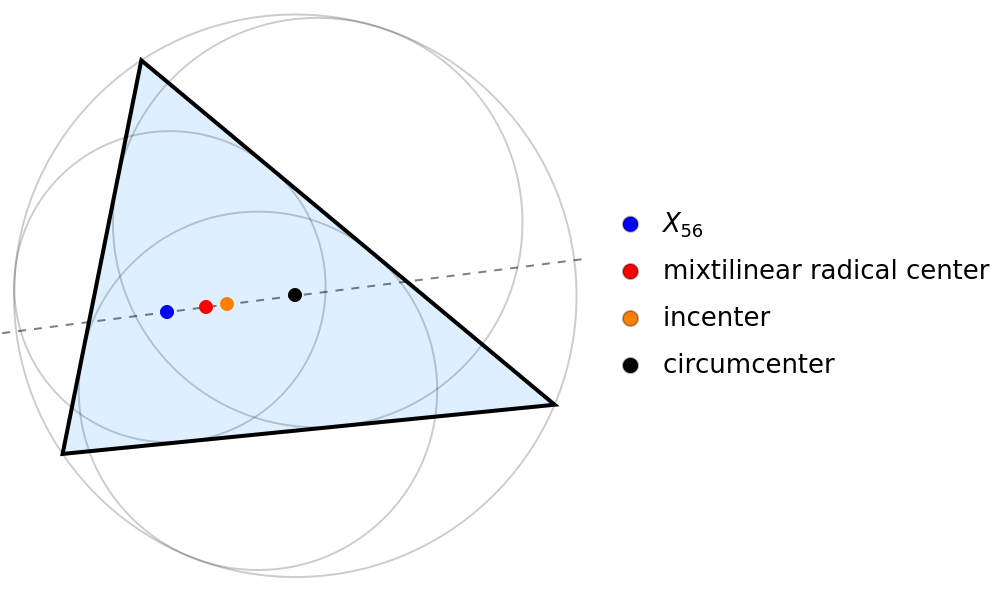 |
This work is licensed under a Creative Commons Attribution 4.0 International License