Wolfram Function Repository

Instant-use add-on functions for the Wolfram Language

Function Repository Resource:

 CausalConnectionGraph

Source Notebook

Generate a graph giving the relations between regions of causally equivalent events in a causal graph

Contributed by: Stephen Wolfram with Jonathan Gorard and Max Piskunov

ResourceFunction["CausalConnectionGraph"][cgf,ti,tf]

generates a graph of relations between causally equivalent regions that are detected at step ti in the causal graph generated by cgf, as determined by outcomes at step tf.

ResourceFunction["CausalConnectionGraph"][cgf,{ti1,ti2},{tf1,tf2}]

considers regions detected between steps ti1 and ti2, with outcomes determined by looking at steps tf1 through tf2.

ResourceFunction["CausalConnectionGraph"][cg,{vi1,…},{vf1,…}]

generates the causal connection graph from the causal graph cg by considering causally equivalent regions among the event nodes vik, as determined by looking at the event nodes vfk.

ResourceFunction["CausalConnectionGraph"][c,i,f,"Full"]

gives the full causal connection graph for every event, not aggregating causally equivalent events.

Details and Options

If the future light cone of A contains the future light cone of B, then there is a directed edge from A to B in the resulting graph.
If the future light cone of A intersects the future light cone of B, but neither contains the other, then there is an undirected edge between A and B in the resulting graph.
Typical forms for the causal graph generator include:
ResourceFunction[“SubstitutionSystemCausalGraph”][rules,init, #] &string substitution system
ResourceFunction[“WolframModel”][rules,init, #, “CausalGraph”] &Wolfram model
ResourceFunction["CausalConnectionGraph"] takes the same options as Graph.

Examples

Basic Examples (2) 

Generate a causal graph:

In[1]:=
Graph[ResourceFunction[ "WolframModel"][{{1, 2}, {2, 3}} -> {{2, 3}, {3, 1}, {4, 1}}, Automatic, 9, "LayeredCausalGraph"], VertexLabels -> Automatic]
Out[1]=

Find the causal connection graph for events at step 3 (there are just two "subuniverses" in this case):

In[2]:=
Graph[ResourceFunction["CausalConnectionGraph"][ ResourceFunction[ "WolframModel"][{{1, 2}, {2, 3}} -> {{2, 3}, {3, 1}, {4, 1}}, Automatic, #, "LayeredCausalGraph"] &, 3, 9], VertexLabels -> Automatic]
Out[2]=

Find the corresponding result for events at step 5:

In[3]:=
Graph[ResourceFunction["CausalConnectionGraph"][ ResourceFunction[ "WolframModel"][{{1, 2}, {2, 3}} -> {{2, 3}, {3, 1}, {4, 1}}, Automatic, #, "LayeredCausalGraph"] &, 5, 11], VertexLabels -> Automatic]
Out[3]=

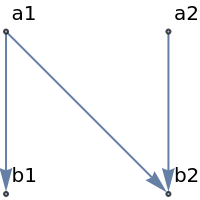
Generate the causal connection graph for a “black hole”, where the future of a1 contains the future of a2, but not the other way around:

In[4]:=
Graph[{a1 -> b1, a1 -> b2, a2 -> b2}, VertexLabels -> Automatic, ImageSize -> 100]
Out[4]=
In[5]:=
ResourceFunction["CausalConnectionGraph"][%, {a1, a2}, {b1, b2}, ImageSize -> 200, VertexLabels -> Automatic]
Out[5]=

Scope (2) 

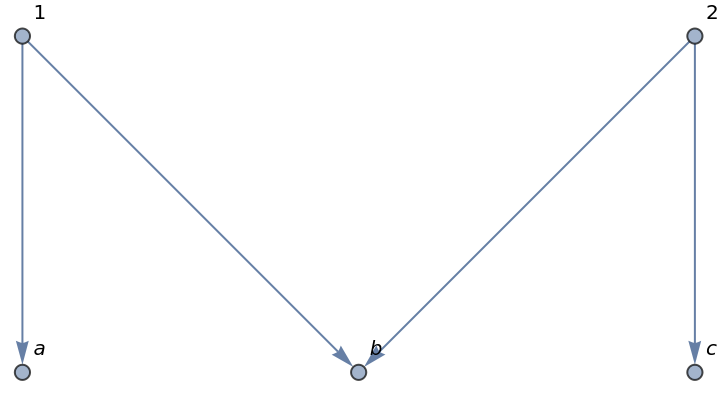
Cases with undirected edges:

In[6]:=
Graph[{1 -> a, 1 -> b, 2 -> b, 2 -> c}, VertexLabels -> Automatic]
Out[6]=
In[7]:=
ResourceFunction[ "CausalConnectionGraph"][%, {1, 2}, {a, b, c}, "Full", VertexLabels -> Automatic]
Out[7]=

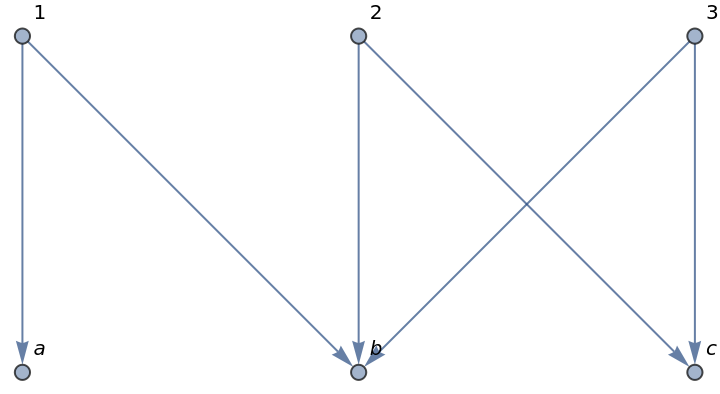
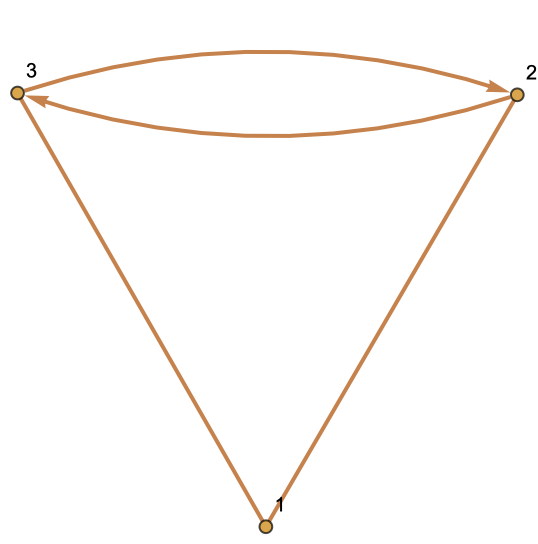
Another example:

In[8]:=
Graph[{1 -> a, 1 -> b, 2 -> b, 2 -> c, 3 -> b, 3 -> c}, VertexLabels -> Automatic]
Out[8]=
In[9]:=
ResourceFunction[ "CausalConnectionGraph"][%, {1, 2, 3}, {a, b, c}, "Full", VertexLabels -> Automatic]
Out[9]=

Version History

  • 1.0.0 – 20 May 2020

Related Resources

License Information