Wolfram Function Repository

Instant-use add-on functions for the Wolfram Language

Function Repository Resource:

 DepthFirstSearch

Source Notebook

Search through a multiway space to find special termination points

Contributed by: Bradley Klee

ResourceFunction["DepthFirstSearch"][graph,init,solutionQ]

performs a depth-first backtracking search from init through the nodes of graph until a terminal state is found to satisfy solutionQ.

ResourceFunction["DepthFirstSearch"][stateUpdate,init,levelData,solutionQ]

searches from init through levelData for a terminal state which satisfies solutionQ, using stateUpdate to generate successive states and backtracking as necessary.

ResourceFunction["DepthFirstSearch"][iterator,init,solutionQ]

builds the search space iteratively from init by applying iterator until a terminal state is found to satisfy solutionQ.

ResourceFunction["DepthFirstSearch"][…,solutionQ,n]

continues the search through the first result, attempting to find up to n distinct results which satisfy solutionQ.

ResourceFunction["DepthFirstSearch"][…,solutionQ,All]

returns all terminal states which satisfy solutionQ.

ResourceFunction["DepthFirstSearch"][…,n,d]

bounds overly deep searches by backtracking whenever the depth equals d.

ResourceFunction["DepthFirstSearch"][…,True]

returns an Association containing all results and search path data under keys "Results" and "Edges" respectively.

Details

Breadth-first and depth-first searches are two similar methods for brute-force solving problems of combinatorial enumeration.
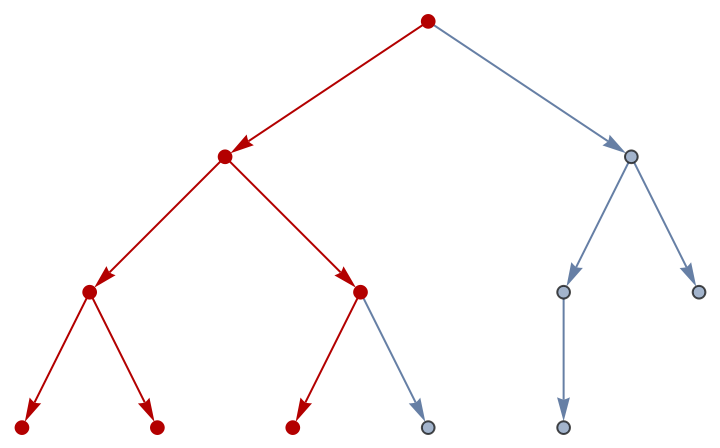
A depth-first search starts at a node, and traverses from child to grandchild downward until either a solution is found, or can be shown not to exist. It will then backtrack up one level, taking the next child at that level and again proceeding downward. Whenever a given level is exhausted of possibilities it goes up a level and over to the next child.
Breadth-first searches in contrast proceed horizontally, visiting all children before going to grandchildren.
This ResourceFunction["DepthFirstSearch"] may be used effectively when only one valid solution is needed; otherwise, a breadth-first search using something like NestWhile can often get the desired results in less time. The reason is that depth-first search incurs an extra cost when backtracking, whereas breadth-first search does not need to backtrack.
ResourceFunction["DepthFirstSearch"] includes a usage that operates on directed graphs. This particular usage compares well with the System function DepthFirstScan, and can be used to obtain similar outputs (see "Properties and Relations" section below).
When traversing an input graph, the algorithm simply follows directed edges immediately to terminal nodes, backtracks to branch points, and continues to take new paths until a solution is found. In practice, this can be done by keeping a path history as a memory stack.
The two primary methods generate partial search graphs, rather than requiring a complete search graph as input. Generation of a search space is done using a state update function, either stateUpdate or iterator.
Function stateUpdate takes an input state as a first argument and draws a second argument from levelData. The list levelData is partitioned into sub-lists containing state differentials as items. An input state at level t is then combined with a differential from the (t+1)th sub-list of levelData to obtain the next state. If the input state is inconsistent with the next differential state from levelData, stateUpdate will return Nothing. This is a failure signal, which causes the algorithm to keep searching for a valid solution. Valid solutions are obtained by combining one differential from each level of levelData, and they must also satisfy the test solutionQ.
Similarly, when a state is input to an iterator, the return is a list of candidate states or an empty list. The empty list is a termination condition, which passes the candidate solution to solutionQ. If the state satisfies solutionQ it will be returned as a positive result. If the state does not satisfy solutionQ, it is ignored and the search continues. As opposed to the method using levelData, enumerating the search space via an iterator allows solutions to be found at any depth.
The test solutionQ should be a function of one variable. Either it takes the name of a terminal vertex on an input graph, or it takes a terminal state created via stateUpdate or iterator. In fact, states generated by stateUpdate or iterator can be thought of as nodes on a search graph.
No two backtracking problems are exactly alike, and results can vary based on ordering of candidate states. Optimizations can often be found by including heuristic-based state selection in either stateUpdate or iterator.

Examples

Basic Examples (3) 

Find a terminal leaf on a binary search tree:

In[1]:=
ResourceFunction["DepthFirstSearch"][ KaryTree[12, DirectedEdges -> True], 1, (True &)]
Out[1]=

Find all terminal leafs on a binary search tree:

In[2]:=
ResourceFunction["DepthFirstSearch"][ KaryTree[12, DirectedEdges -> True], 1, (True &), All]
Out[2]=

Depict the search up to three leafs:

In[3]:=
HighlightGraph[KaryTree[12, DirectedEdges -> True], Graph[ ResourceFunction["DepthFirstSearch"][ KaryTree[12, DirectedEdges -> True], 1, (True &), 3, True]["Edges"]]]
Out[3]=

Find a partition of the first seven integers into two sets with equal sums:

In[4]:=
ResourceFunction["DepthFirstSearch"][ Function[MapThread[Append, {#1, #2}] /. {0 -> Nothing}], {{}, {}}, IdentityMatrix[2] # & /@ Range[7], SameQ @@ (Total /@ #) &]
Out[4]=

Find another solution to the same problem:

In[5]:=
ResourceFunction["DepthFirstSearch"][ Function[MapThread[Append, {#1, #2}] /. {0 -> Nothing}], {{}, {}}, IdentityMatrix[2] # & /@ Range[7], SameQ @@ (Total /@ #) &, 2]
Out[5]=

Find all solutions:

In[6]:=
ResourceFunction["DepthFirstSearch"][ Function[MapThread[Append, {#1, #2}] /. {0 -> Nothing}], {{}, {}}, IdentityMatrix[2] # & /@ Range[7], SameQ @@ (Total /@ #) &, All]
Out[6]=

Find a Hamiltonian path along the edges of a cube:

In[7]:=
ResourceFunction["DepthFirstSearch"][ Function[{state}, If[SameQ[#, {}], {}, Append[state, #]] & /@ Complement[ VertexOutComponent[ PolyhedronData["Cube", "Skeleton"], Last[state], {1}], state]], {1}, And[Length[#] == 8, GraphDistance[ PolyhedronData["Cube", "Skeleton"], First[#], Last[#]] == 1] &]
Out[7]=

Scope (2) 

Depict a search for the deepest leaf of a random TreeGraph:

In[8]:=
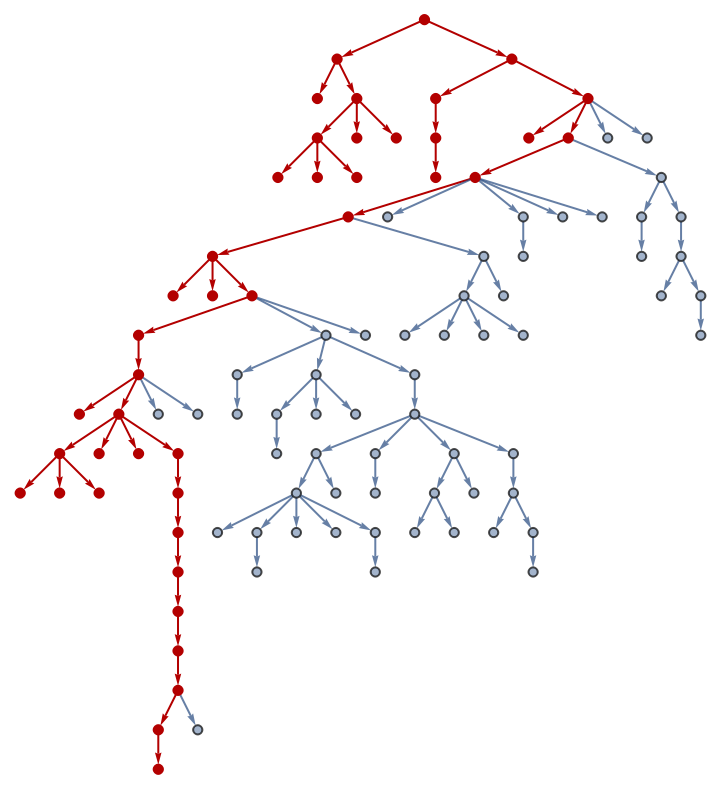
With[{t0 = (SeedRandom[123324]; RandomTree[100]), g0 = (SeedRandom[123324]; IndexGraph[ TreeGraph[RandomTree[100]]])}, HighlightGraph[g0, Graph[ResourceFunction["DepthFirstSearch"][g0, 100, SameQ[GraphDistance[g0, 100, #], TreeDepth[t0]] &, 1, True]["Edges"]]]]
Out[8]=

Find and depict 20 results at depth less than or equal to 10:

In[9]:=
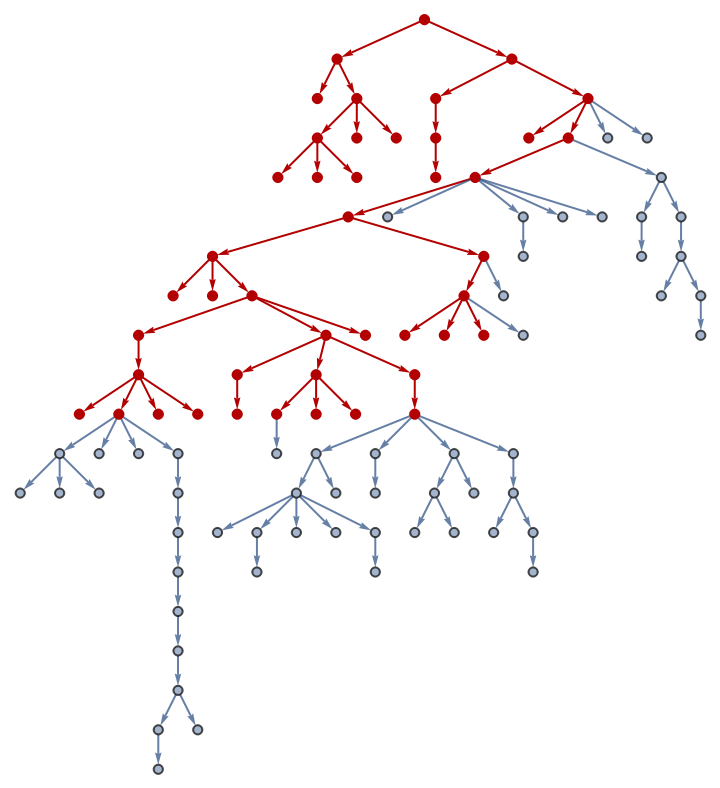
With[{t0 = (SeedRandom[123324]; RandomTree[100]), g0 = (SeedRandom[123324]; IndexGraph[ TreeGraph[RandomTree[100]]])}, HighlightGraph[g0, Graph[ResourceFunction["DepthFirstSearch"][g0, 100, True &, 20, 10, True]["Edges"]]]]
Out[9]=

Properties and Relations (2) 

Highlight a search Graph according to its progress in finding All results:

In[10]:=
Module[{g0 = (SeedRandom[123324]; IndexGraph[ TreeGraph[RandomTree[100]], VertexSize -> Small, VertexStyle -> Directive[LightGray, EdgeForm[Gray]], EdgeStyle -> Directive[Thick, Arrowheads[0.025]]]), leafCount, progress}, leafCount = CountsBy[VertexList[g0], VertexOutDegree[g0, #] &][0]; progress = Map[ResourceFunction["DepthFirstSearch"][g0, 100, (True &), #, True] &, Range[leafCount]]; HighlightGraph[g0, MapThread[Style[#1, #2] &, {Prepend[Complement @@ Reverse[#] & /@ Partition[ #["Edges"] & /@ progress, 2, 1], progress[[1]]["Edges"]] , Darker@Hue[#/(leafCount + 5) ] & /@ Range[leafCount]}]]]
Out[10]=

Compare with DepthFirstScan:

In[11]:=
Module[{g0 = (SeedRandom[123324]; IndexGraph[ TreeGraph[RandomTree[100]], VertexSize -> Small, VertexStyle -> Directive[LightGray, EdgeForm[Gray]], EdgeStyle -> Directive[Thick, Arrowheads[0.025]]]), leafCount, progress, ind = 1}, leafCount = CountsBy[VertexList[g0], VertexOutDegree[g0, #] &][0]; progress = Reap[DepthFirstScan[g0, 100, {"PrevisitVertex" -> ((Sow[# -> ind++]) &)}]][[2, 1]]; HighlightGraph[g0, Reverse@MapThread[ Style[DirectedEdge @@@ Partition[#1, 2, 1], #2] &, {FindShortestPath[g0, 100, #] & /@ SortBy[Select[ VertexList[g0], VertexOutDegree[g0, #] == 0 &], # /. progress &] , Darker@Hue[#/(leafCount + 5) ] & /@ Range[leafCount]}]]]
Out[11]=

List all possible partitions of integer 10 into three lesser integers:

In[12]:=
ResourceFunction["DepthFirstSearch"][ Function[With[{tot = #1[[2]] + #2}, If[tot <= 10, Append[#1[[1]], #2] -> tot, Nothing]]], {} -> 0, ConstantArray[Range[8], 3], Last[#] == 10 &, All]
Out[12]=

Another way to solve the same problem:

In[13]:=
ResourceFunction["DepthFirstSearch"][ Function[{state}, With[{ tot = Total[state[[1]]], len = Length[state[[1]]]}, If[len == 3, {}, Map[Append[state[[1]], #] -> (state[[2]] + #) &, Range[1, (10 - tot) - (3 - (len + 1))]]]]], {} -> 0, Last[#] == 10 &, All]
Out[13]=

Prove non-minimality of the first method:

In[14]:=
With[{ e1 = ResourceFunction["DepthFirstSearch"][ Function[With[{tot = #1[[2]] + #2}, If[tot <= 10, Append[#1[[1]], #2] -> tot, Nothing]]], {} -> 0, ConstantArray[Range[8], 3], Last[#] == 10 &, All, True]["Edges"], e2 = ResourceFunction["DepthFirstSearch"][ Function[{state}, With[{ tot = Total[state[[1]]], len = Length[state[[1]]]}, If[len == 3, {}, Map[Append[state[[1]], #] -> (state[[2]] + #) &, Range[1, (10 - tot) - (3 - (len + 1))]]]]], {} -> 0, Last[#] == 10 &, All, True]["Edges"]}, And[UnsameQ[e1, e2], SubsetQ[e1, e2]]]
Out[14]=

Possible Issues (3) 

Undirected graphs have no terminal nodes, so are disallowed:

In[15]:=
TimeConstrained[ ResourceFunction["DepthFirstSearch"][CycleGraph[4], 1, True &, All], 5]
Out[15]=

If the search space is cyclic, the search can possibly hang:

In[16]:=
TimeConstrained[ ResourceFunction["DepthFirstSearch"][Function[{n}, If[IntegerQ[n], {n/2, 3 n + 1}, {}]], 1, True &, All], 5]
Out[16]=

Introducing a cut-off limits the number of loops a search can go through:

In[17]:=
Grid[Partition[ Graph[ResourceFunction["DepthFirstSearch"][ Function[{n}, If[IntegerQ[n], {n/2, 3 n + 1}, {}]], 1, True &, All, #, True]["Edges"], ImageSize -> 120] & /@ Range[12], 4], Spacings -> {2, 2}, Frame -> All, FrameStyle -> LightGray]
Out[17]=

To find all relevant results, it may be necessary to search from multiple initial conditions:

In[18]:=
With[{g1 = (SeedRandom[2414323]; Graph[ResourceFunction["ToDirectedAcyclicGraph" ][#, VertexList[#][[{1, 2}]]], VertexCoordinates -> Automatic, GraphLayout -> "LayeredDigraphEmbedding", AspectRatio -> 2/3] &[ WeaklyConnectedGraphComponents[ RandomGraph[{300, 350}]][[1]]])}, HighlightGraph[g1, { Style[Complement[#[[1]], #[[2]]], Blue], Style[Complement[#[[2]], #[[1]]], Darker@Green], Style[Intersection[#[[2]], #[[1]]], Blend[{Blue, Green}]]}] &@( ResourceFunction["DepthFirstSearch"][g1, #, True &, All, True][ "Edges"] & /@ {1, 23})]
Out[18]=

Neat Examples (4) 

Find a 10×10 periodic pattern to be consistent with five binary templates:

In[19]:=
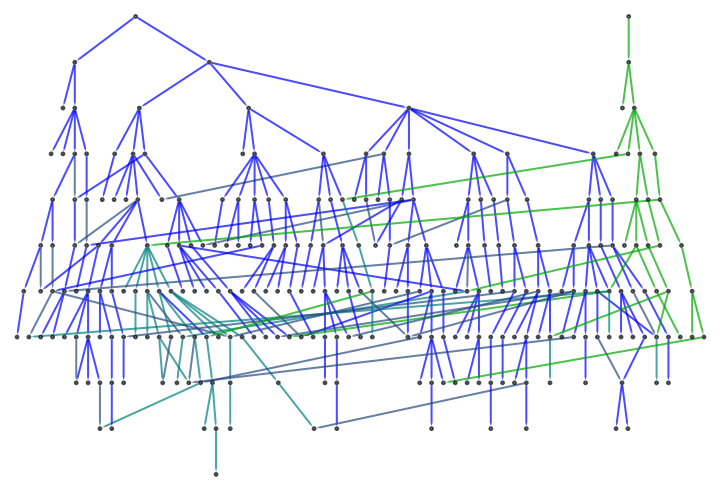
With[{periodicTemplates = {{{1, 1, 1}, {1, 0, 1}, {1, 1, 1}}, {{1, 1, 0}, {0, 1, 1}, {1, 1, 1}}, {{1, 0, 1}, {1, 1, 1}, {1, 1, 0}}, {{0, 1, 1}, {1, 1, 1}, {1, 0, 1}}, {{1, 1, 1}, {1, 1, 0}, {0, 1, 1}}}, templateExpand = Function[{template, size}, With[{colLen = Part[size, 2] + Part[ Dimensions[template], 2] - 1}, Catenate[ Outer[ Function[{row, col}, Part[ RotateRight[ Map[RotateRight[#, col]& , Join[ Map[PadRight[#, colLen, Blank[]]& , template], Table[ ConstantArray[ Blank[], colLen], {Part[size, 1] - 1}]]], row], Span[-Part[size, 1], -1], Span[-Part[size, 2], -1]]], Range[0, Part[size, 1] + Part[ Dimensions[template], 1] - 2], Range[0, Part[size, 2] + Part[ Dimensions[template], 2] - 2], 1]]]], rowsCombine = Function[{r1, r2}, Catch[ MapThread[ Function[{x, y}, Switch[{x, y}, { Verbatim[ Blank[]], Blank[]}, y, { Blank[], Verbatim[ Blank[]]}, x, { Blank[], Blank[]}, If[x === y, x, Throw[Nothing]]]], {r1, r2}]]], size = 10}, Labeled[ArrayPlot[Partition[ ResourceFunction["DepthFirstSearch"][rowsCombine, ConstantArray[_, size^2], Reverse[Union[#] ] & /@ Transpose[(Catenate /@ templateExpand[#, {size, size}] ) & /@ periodicTemplates], True &], size]], Row[ArrayPlot[#, ImageSize -> 40] & /@ periodicTemplates, Spacer[5]], Spacings -> {1, 1}]]
Out[19]=

Highlight the depth-first, single-result search as a subgraph of the comprehensive search graph:

In[20]:=
Module[{periodicTemplates = {{{1, 1, 1}, {1, 0, 1}, {1, 1, 1}}, {{1, 1, 0}, {0, 1, 1}, {1, 1, 1}}, {{1, 0, 1}, {1, 1, 1}, {1, 1, 0}}, {{ 0, 1, 1}, {1, 1, 1}, {1, 0, 1}}, {{1, 1, 1}, {1, 1, 0}, {0, 1, 1}}}, templateExpand = Function[{template, size}, With[{colLen = Part[size, 2] + Part[ Dimensions[template], 2] - 1}, Catenate[ Outer[ Function[{row, col}, Part[ RotateRight[ Map[RotateRight[#, col]& , Join[ Map[PadRight[#, colLen, Blank[]]& , template], Table[ ConstantArray[ Blank[], colLen], {Part[size, 1] - 1}]]], row], Span[-Part[size, 1], -1], Span[-Part[size, 2], -1]]], Range[0, Part[size, 1] + Part[ Dimensions[template], 1] - 2], Range[0, Part[size, 2] + Part[ Dimensions[template], 2] - 2], 1]]]], rowsCombine = Function[{r1, r2}, Catch[ MapThread[ Function[{x, y}, Switch[{x, y}, { Verbatim[ Blank[]], Blank[]}, y, { Blank[], Verbatim[ Blank[]]}, x, { Blank[], Blank[]}, If[x === y, x, Throw[Nothing]]]], {r1, r2}]]], size = 10, init, levelData}, init = ConstantArray[_, size^2]; levelData = Reverse[Union[#]] & /@ Transpose[ (Catenate /@ templateExpand[#, {size, size}] ) & /@ periodicTemplates]; With[{ g1 = Graph[ResourceFunction["DepthFirstSearch"][ rowsCombine, init, levelData, True &, All, True]["Edges"], GraphLayout -> "LayeredDigraphEmbedding", ImageSize -> 600, AspectRatio -> 2/3, VertexSize -> 1/4], g2 = Graph[ResourceFunction["DepthFirstSearch"][rowsCombine, init, levelData, True &, 1, True]["Edges"]] }, HighlightGraph[ VertexReplace[g1, vert_ :> (vert /. {Verbatim[_] -> x})], VertexReplace[g2, vert_ :> (vert /. {Verbatim[_] -> x})]]]]
Out[20]=

Find and depict a symmetric arrangement of 8 non-attacking queens on a standard chess board:

In[21]:=
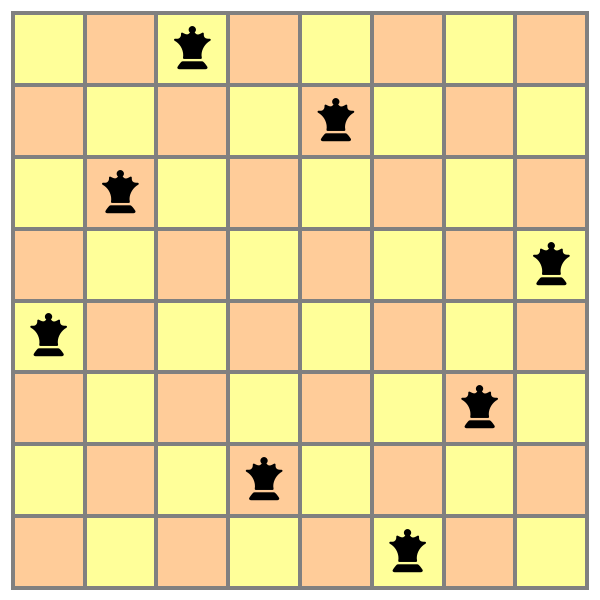
With[{rowsCombine = Function[{r1, r2}, Catch[ MapThread[ Function[{x, y}, Switch[{x, y}, { Verbatim[ Blank[]], Blank[]}, y, { Blank[], Verbatim[ Blank[]]}, x, { Blank[], Blank[]}, If[x === y, x, Throw[Nothing]]]], {r1, r2}]]], queenCoversData = Function[{size}, Table[ Flatten[ ReplacePart[ Table[ If[ Or[i == k, j == l, i + j == k + l, i - j == k - l], 0, Blank[]], {i, Part[size, 1]}, {j, Part[size, 2]}], {k, l} -> 1]], {k, Part[size, 1]}, {l, Part[size, 2]}]], queensDepict = ResourceFunction["CharacterArrayPlot"][ 2 Partition[#, 8] + Table[ Mod[i + j, 2], {i, 8}, {j, 8}], ColorRules -> {Pattern[x, Blank[]] :> <|0 -> Lighter[Yellow, 0.6], 1 -> Lighter[Orange, 0.6]|>[ Mod[x, 2]]}, "CharacterRules" -> {1 -> "", 0 -> "", Pattern[x, Blank[]] :> FromCharacterCode[9819]}, "CharacterStyleRules" -> {Pattern[x, Blank[]] :> {20, Black}}, MeshStyle -> Directive[Gray, Thick], ImageSize -> 300]& }, queensDepict[ ResourceFunction["DepthFirstSearch"][ rowsCombine, ConstantArray[_, 64], queenCoversData[{8, 8}], SameQ[Partition[#, 8], Reverse /@ Reverse[Partition[#, 8]]] &]]]
Out[21]=

Find and depict a Knight's tour around a 5×5 board:

In[22]:=
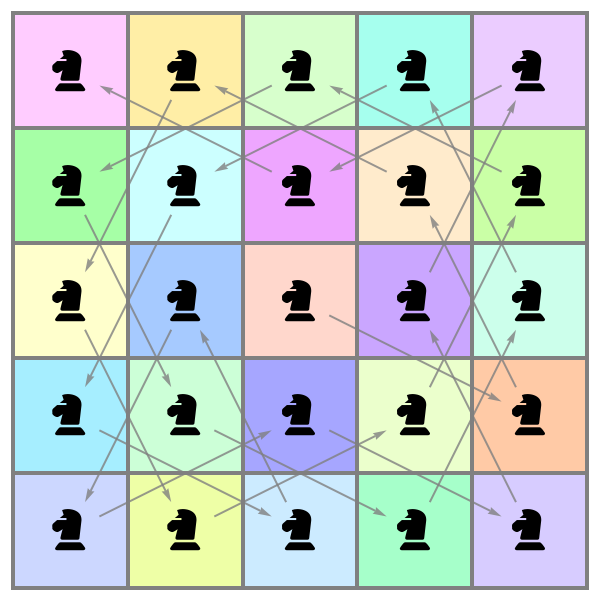
With[{moves = {{-2, -1}, {-2, 1}, {-1, -2}, {-1, 2}, {1, -2}, {1, 2}, {2, -1}, {2, 1}}, iterateWalk = Function[{board, moves}, With[{max = Max[board], pos = Part[ Position[board, Max[board]], 1]}, Map[ReplacePart[board, # -> max + 1]& , Select[ Map[pos + #& , RandomSample[moves]], If[ Apply[And, Thread[ Inequality[ Dimensions[board], GreaterEqual, #, Greater, {0, 0}]]], Part[board, Apply[Sequence, #]] == 0, False]& ]]]], knightsDepict = Show[{ (ResourceFunction["CharacterArrayPlot"][#, ColorRules -> {Pattern[x, Blank[]] :> (If[Mod[x, 2] == 0, Lighter[#, 0.65], Lighter[#, 0.8]]& )[ Hue[x/30]]}, "CharacterRules" -> {Pattern[x, Blank[]] :> ""}, MeshStyle -> Directive[Gray, Thick], ImageSize -> 300]& )[#], Function[{sol}, (Graph[ EdgeList[#], VertexShape -> Style[ FromCharacterCode[9822], Black, 20], VertexCoordinates -> Map[# -> Reverse[{-1, 1} #]& , VertexList[#]], VertexSize -> 1/2, PerformanceGoal -> "Quality", EdgeStyle -> Directive[ Opacity[0.8, Gray]]]& )[ PathGraph[ Map[Part[ Position[sol, #], 1]& , Range[25]], DirectedEdges -> True]]][#]}]& }, knightsDepict@ResourceFunction["DepthFirstSearch"][ Function[iterateWalk[#, moves]], ReplacePart[ConstantArray[0, {5, 5}], {3, 3} -> 1], Max[#] == 25 &, 1]]
Out[22]=

Search for a corner-to-corner path across a RandomSierpinskiMaze:

In[23]:=
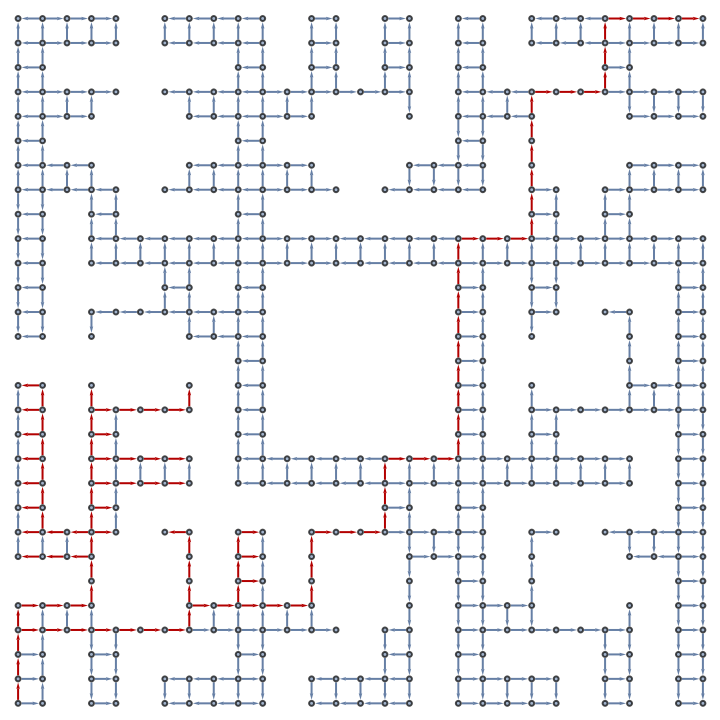
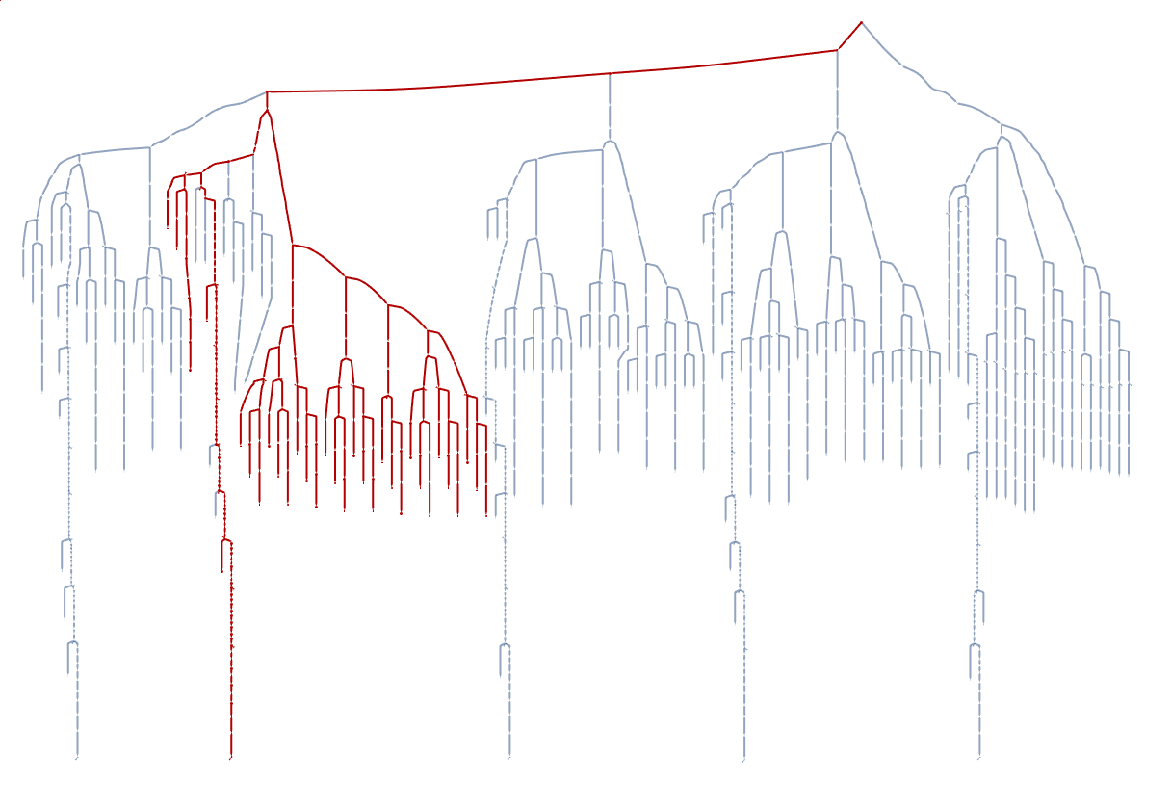
With[{g1 = (SeedRandom["mazeTest"]; ResourceFunction["ToDirectedAcyclicGraph"][ ResourceFunction["RandomSierpinskiMaze"][2, AdjacencyGraph], {{1, 1}}])}, Graph[HighlightGraph[g1, ResourceFunction["DepthFirstSearch"][g1, {1, 1}, SameQ @@ # &, True]["Edges"] ], VertexCoordinates -> (# -> # & /@ VertexList[g1])]]
Out[23]=

Optimize the search by introducing a "North-first" heuristic:

In[24]:=
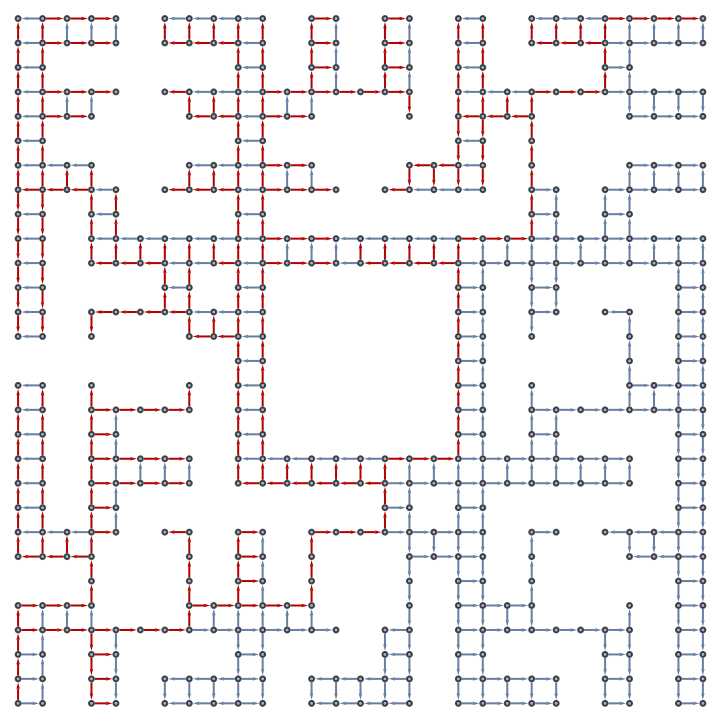
With[{g1 = (SeedRandom["mazeTest"]; ResourceFunction["ToDirectedAcyclicGraph"][ ResourceFunction["RandomSierpinskiMaze"][ 2, AdjacencyGraph], {{1, 1}}])}, Graph[HighlightGraph[g1, ResourceFunction["DepthFirstSearch"][ Association[# -> SortBy[ Cases[EdgeList[g1], DirectedEdge[#, x_] :> x], {-#[[2]], -#[[1]]} &] & /@ Sort[VertexList[g1]]], {1, 1}, SameQ @@ # &, True]["Edges"]], VertexCoordinates -> (# -> # & /@ VertexList[g1])]]
Out[24]=

Publisher

Brad Klee

Version History

  • 1.0.0 – 25 July 2022

Related Resources

License Information