Wolfram Function Repository
Instant-use add-on functions for the Wolfram Language
Function Repository Resource:
Find explicit sets of rules for computational systems
ResourceFunction["ComputationalSystemRules"][sys] returns an explicit set of rules for the computational system sys. |
| CellularAutomaton[spec] | cellular automaton |
| TuringMachine[spec] | Turing machine |
| SubstitutionSystem[spec] | substitution system |
| BooleanFunction[spec] | Boolean function |
Get the explicit set of rules for a cellular automaton:
| In[1]:= |
|
| Out[1]= |
|
Evolution of the system specified by the explicit rules:
| In[2]:= |
|
| Out[2]= |

|
Compare with the canonical representation of the same system:
| In[3]:= |
|
| Out[3]= |

|
Explicit rules for a Turing machine:
| In[4]:= |
|
| Out[4]= |
|
Both representations yield the same evolution:
| In[5]:= |
|
| Out[5]= |

|
Boolean function in two variables:
| In[6]:= |
|
| Out[6]= |
|
| In[7]:= |
|
| Out[7]= |

|
String substitution system:
| In[8]:= |
|
| In[9]:= |
|
| Out[9]= |
|
An evolution step:
| In[10]:= |
|
| Out[10]= |
|
| In[11]:= |
|
| Out[11]= |
|
| In[12]:= |
|
| Out[12]= |
|
Various forms of cellular automata, including elementary rules:
| In[13]:= |
|
| Out[13]= |
|
Multi-color rules:
| In[14]:= |
|
| Out[14]= |
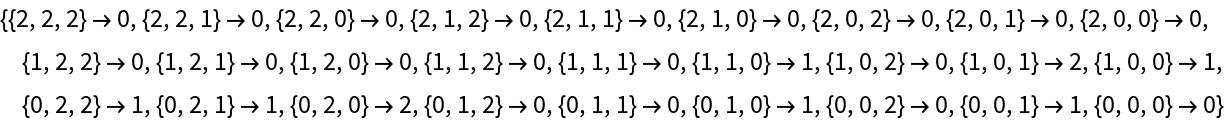
|
Neighborhood rules:
| In[15]:= |
|
| Out[15]= |
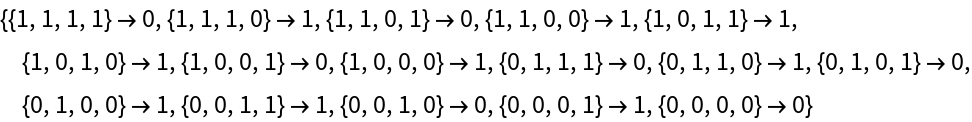
|
Rules specified using an association:
| In[16]:= |
|
| Out[16]= |
|
| In[17]:= |
|
| Out[17]= |
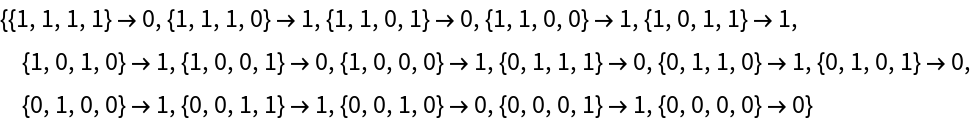
|
Turing machine rule 2506:
| In[18]:= |
|
| Out[18]= |
|
Turing machine with more than two colors:
| In[19]:= |
|
| Out[19]= |
|
| In[20]:= |
![ResourceFunction["ComputationalSystemRules"][
TuringMachine[{{1, 2} -> {1, 1, -1}, {1, 1} -> {1, 2, -1}, {1, 0} -> {2, 1, 1}, {2, 2} -> {1, 0, 1}, {2, 1} -> {2, 2, 1}, {2, 0} -> {1, 2, -1}}]]](https://www.wolframcloud.com/obj/resourcesystem/images/da0/da0ee8f1-f382-403d-8c98-6a51594024c4/76c7629edeba0a52.png)
|
| Out[20]= |
|
ComputationalSystemRules does not parse system specifications beyond those acceptable to RulePlot:
| In[21]:= |
|
| In[22]:= |
|
| Out[22]= |
|
| In[23]:= |
|
| Out[23]= |
|
Use a system that can be handled by RulePlot:
| In[24]:= |
|
| In[25]:= |
|
| Out[25]= |
|
| In[26]:= |
|
| Out[26]= |

|
ComputationalSystemRules does not handle totalistic cellular automata:
| In[27]:= |
|
| Out[27]= |
|
This work is licensed under a Creative Commons Attribution 4.0 International License