Wolfram Function Repository
Instant-use add-on functions for the Wolfram Language
Function Repository Resource:
Produce causal graphs by dynamically triangulating a flat (Minkowski) spacetime
ResourceFunction["FlatSpacetimeTriangulation"][dim,meas] produces a dynamical triangulation of a flat (Minkowski) spacetime of dimension (dim-1)+1 into simplices with maximum measure (e.g. area, volume, etc.) meas. | |
ResourceFunction["FlatSpacetimeTriangulation"][dim,meas,"prop"] gives the property "prop" for the specified flat (Minkowski) spacetime triangulation. |
| "CausalGraphFull" | full causal partial-order graph (before transitive reduction) |
| "CausalGraph" | transitively reduced causal partial-order graph |
| "TriangulatedCausalGraphFull" | full causal partial-order graph using only triangulation edges (before transitive reduction) |
| "TriangulatedCausalGraph" | transitively reduced triangulated causal partial-order graph |
| "Points" | plot of the points in the triangulation (without causal edges) |
| "PointsList" | list of spacetime coordinates of all points in the triangulation |
| "PointsCount" | number of points in the triangulation |
| "Dimensions" | number of dimensions in the continuum spacetime approximation |
| "TriangulatedEdgeList" | list of (undirected) edges that appear in the triangulation of the spacetime surface |
| "TriangulatedEdgeCount" | number of (undirected) edges that appear in the triangulation of the spacetime surface |
| "MaximumCellMeasure" | maximum measure (e.g. area, volume, etc.) meas of the simplices appearing in the triangulation |
| "TotalEdgeCount" | total number of causal edges (before transitive reduction) |
| "ReducedEdgeCount" | number of transitively reduced causal edges |
| "TotalTriangulatedEdgeCount" | total number of causal edges that are also triangulation edges (before transitive reduction) |
| "ReducedTriangulatedEdgeCount" | number of transitively reduced causal edges that are also triangulation edges |
| "PureCausalGraphFull" | full causal partial-order graph (before transitive reduction) with vertex coordinate information removed |
| "PureCausalGraph" | transitively reduced causal partial-order graph with vertex coordinate information removed |
| "PureTriangulatedCausalGraphFull" | full causal partial-order graph using only triangulation edges (before transitive reduction) with vertex coordinate information removed |
| "PureTriangulatedCausalGraph" | transitively reduced triangulated causal partial-order graph with vertex coordinate information removed |
| "MeshRegion" | mesh region corresponding to the triangulated spacetime surface |
| "MeshConnectivityGraph" | connectivity graph of the mesh region corresponding to the triangulated spacetime surface |
| "Properties" | list of properties |
Produce a triangulation of a 1+1-dimensional flat (Minkowski) spacetime into simplices of measure (area) up to 0.05:
| In[1]:= |
|
| Out[1]= |
|
Show the causal graph:
| In[2]:= |
|
| Out[2]= |
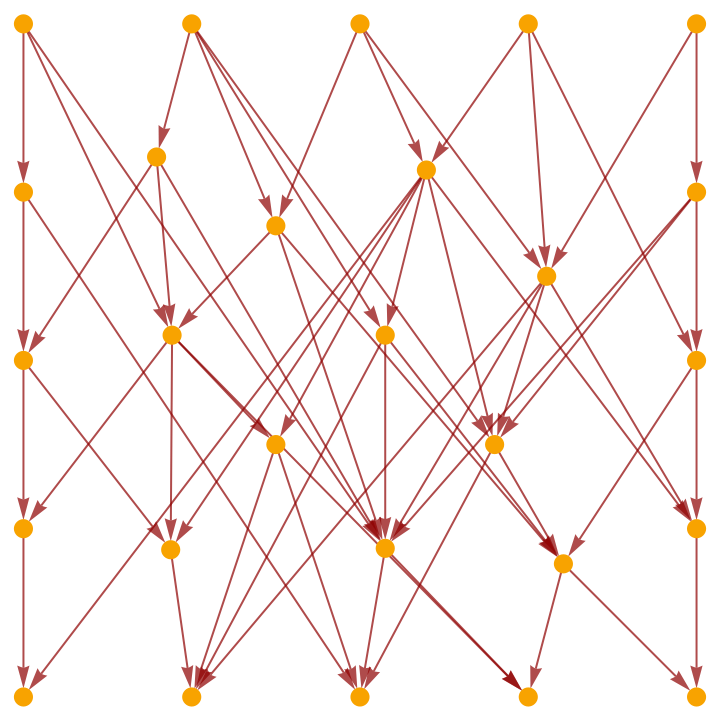
|
Show the full causal graph (without transitive reduction):
| In[3]:= |
|
| Out[3]= |

|
Show the causal graph using only triangulation edges:
| In[4]:= |
|
| Out[4]= |
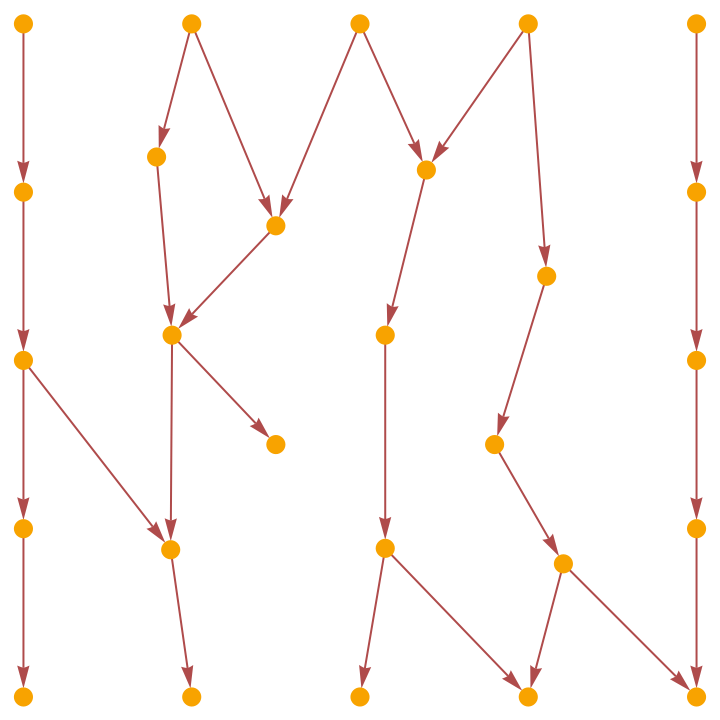
|
Produce a triangulation of a 1+1-dimensional flat (Minkowski) spacetime into smaller simplices of measure (area) up to 0.01 instead:
| In[5]:= |
|
| Out[5]= |
|
Show the causal graph:
| In[6]:= |
|
| Out[6]= |
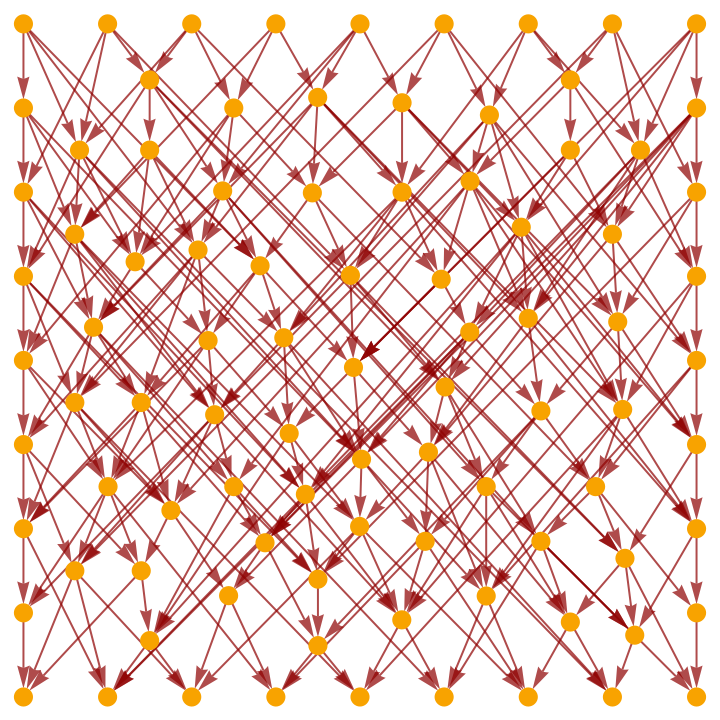
|
Show the mesh region corresponding to the triangulated spacetime surface:
| In[7]:= |
|
| Out[7]= |

|
Show the connectivity graph of this mesh region:
| In[8]:= |
|
| Out[8]= |

|
Show the full triangulated causal graph (without transitive reduction):
| In[9]:= |
|
| Out[9]= |
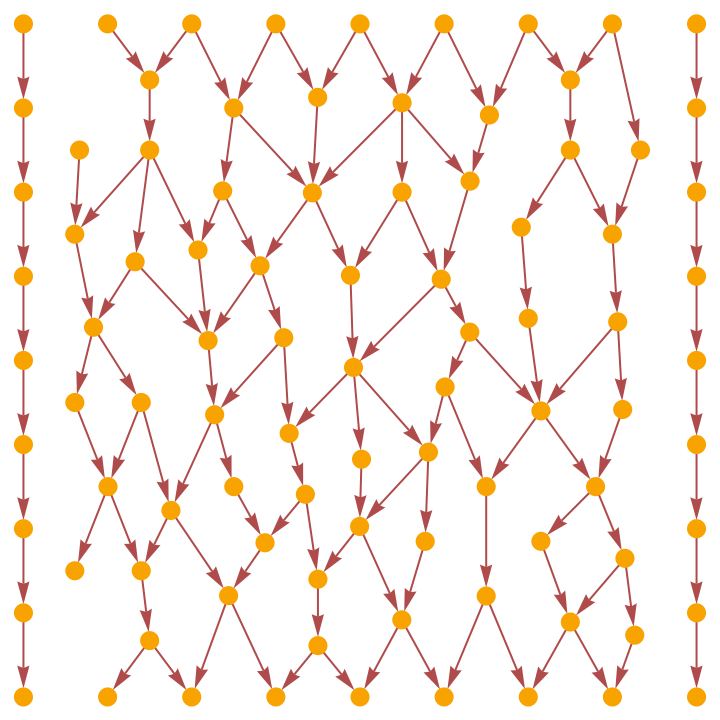
|
Produce a triangulation of a 2+1-dimensional flat (Minkowski) spacetime into simplices of measure (volume) up to 1:
| In[10]:= |
|
| Out[10]= |

|
Show the causal graph:
| In[11]:= |
|
| Out[11]= |
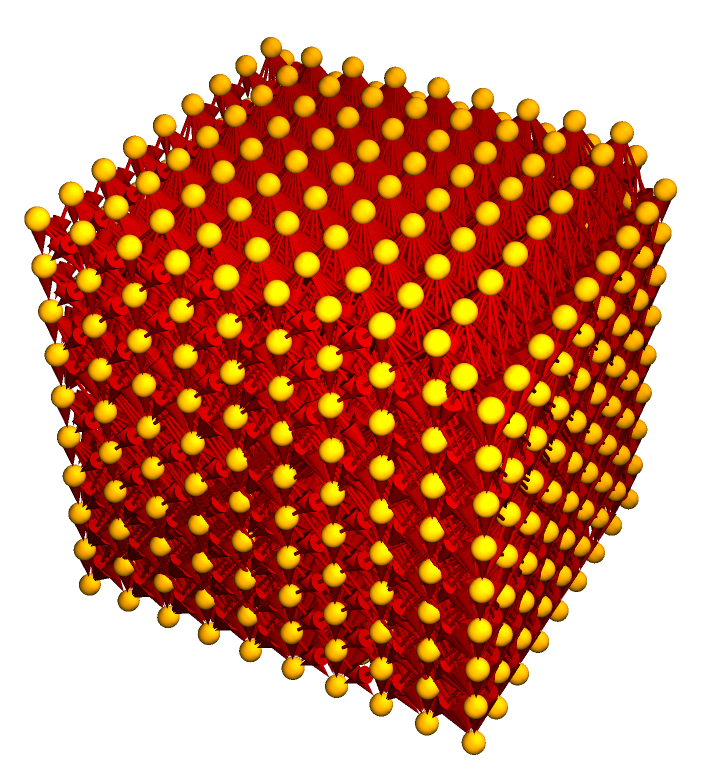
|
Show the pure causal graph (with vertex coordinate information removed):
| In[12]:= |
|
| Out[12]= |
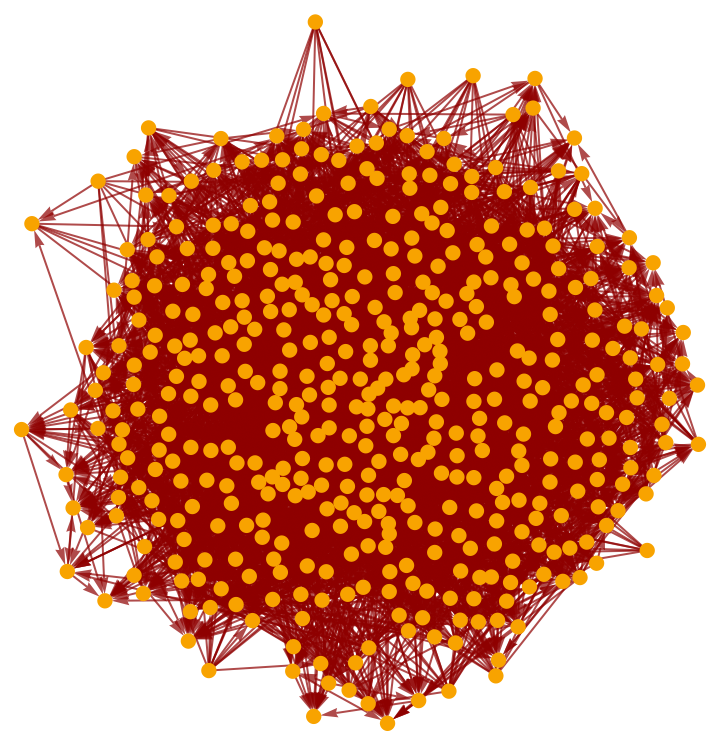
|
Show only the pure triangulated causal graph (with vertex coordinate information removed):
| In[13]:= |
|
| Out[13]= |
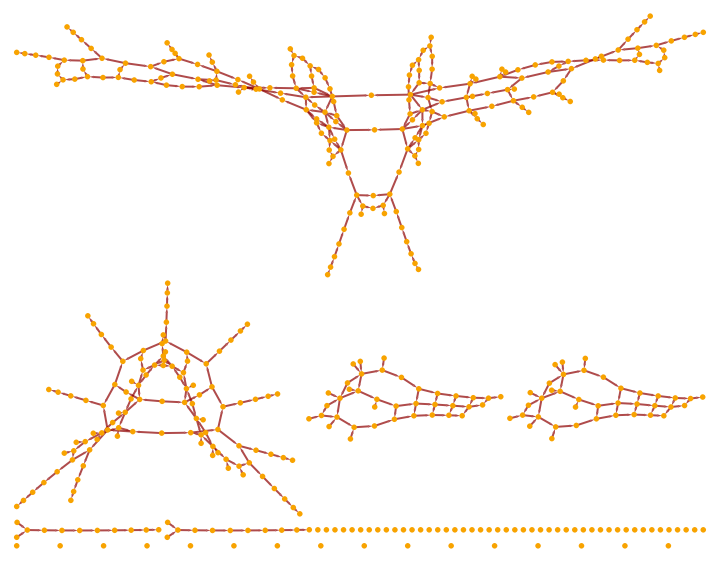
|
Triangulations can be produced for 0+1-dimensional spacetimes:
| In[14]:= |
|
| Out[14]= |
|
Show the pure causal graph:
| In[15]:= |
|
| Out[15]= |

|
Produce a triangulation of a 1+1-dimensional spacetime:
| In[16]:= |
|
| Out[16]= |
|
Show the pure causal graph:
| In[17]:= |
|
| Out[17]= |

|
Produce a triangulation of a 2+1-dimensional spacetime:
| In[18]:= |
|
| Out[18]= |

|
Show the pure causal graph:
| In[19]:= |
|
| Out[19]= |
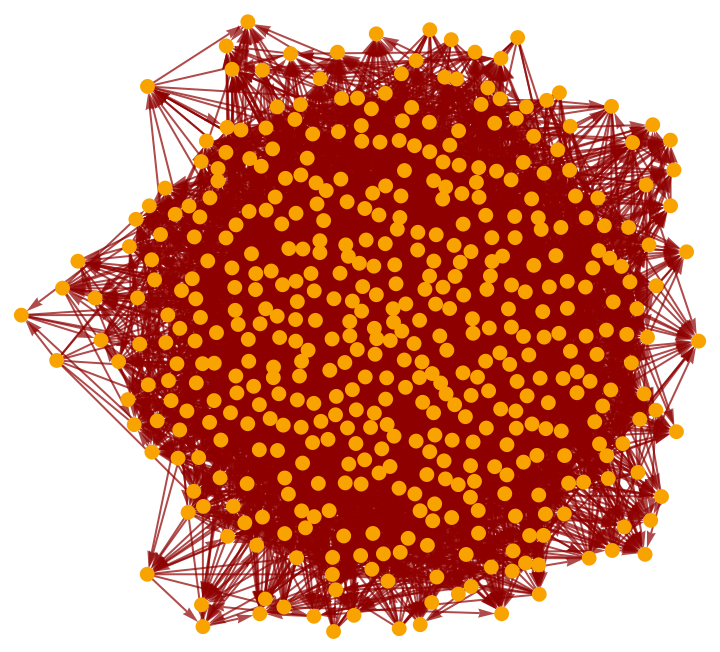
|
Properties can be requested directly from FlatSpacetimeTriangulation:
| In[20]:= |
|
| Out[20]= |
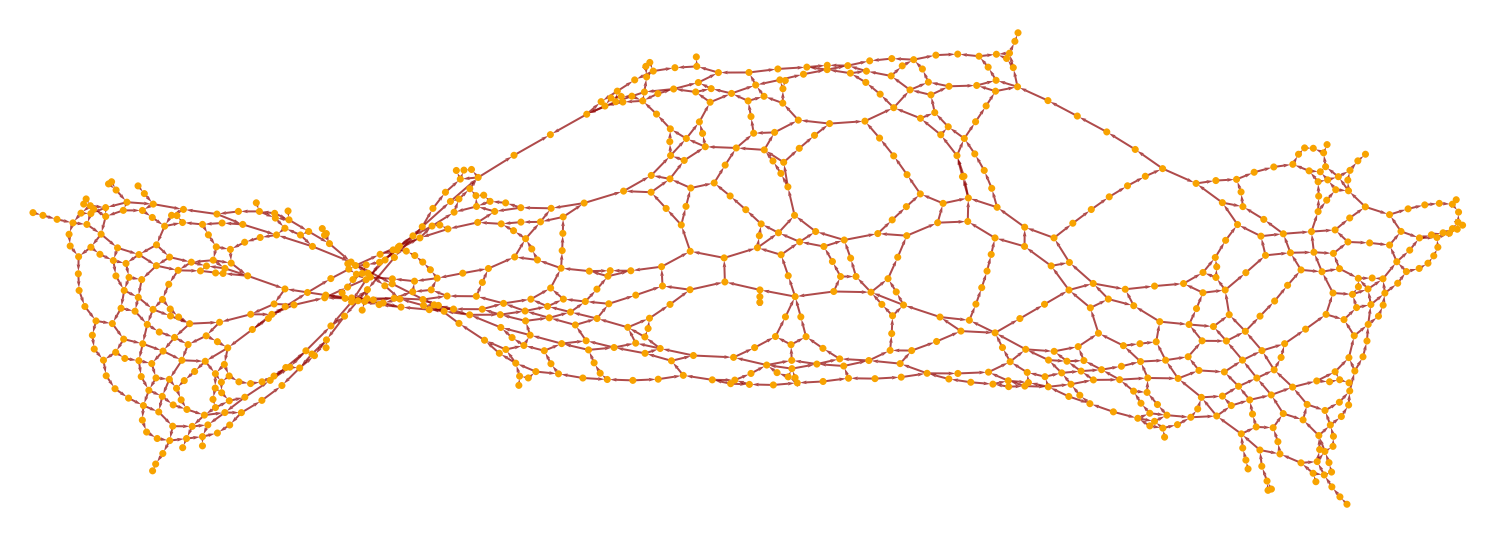
|
Produce a triangulation of a 1+1-dimensional flat (Minkowski) spacetime into simplices of measure (area) up to 0.005:
| In[21]:= |
|
| Out[21]= |
|
Show the complete list of properties:
| In[22]:= |
|
| Out[22]= |

|
Show the full causal graph:
| In[23]:= |
|
| Out[23]= |

|
Show the transitively-reduced causal graph:
| In[24]:= |
|
| Out[24]= |
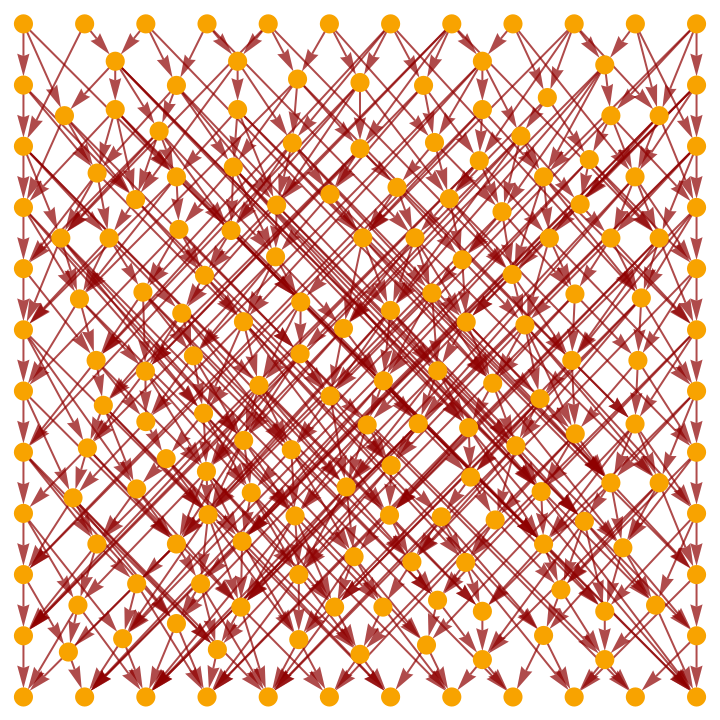
|
Show the full causal graph using only triangulation edges:
| In[25]:= |
|
| Out[25]= |
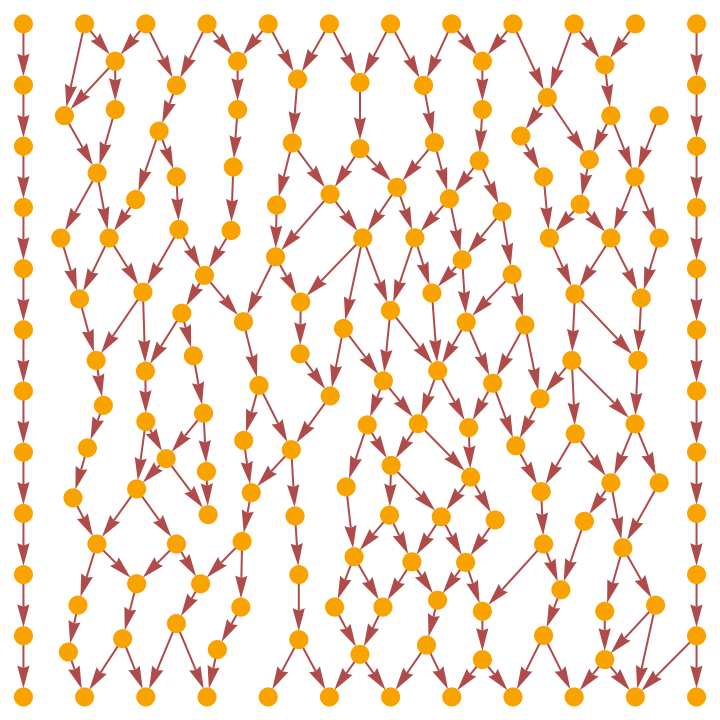
|
Show the transitively-reduced causal graph using only triangulation edges:
| In[26]:= |
|
| Out[26]= |
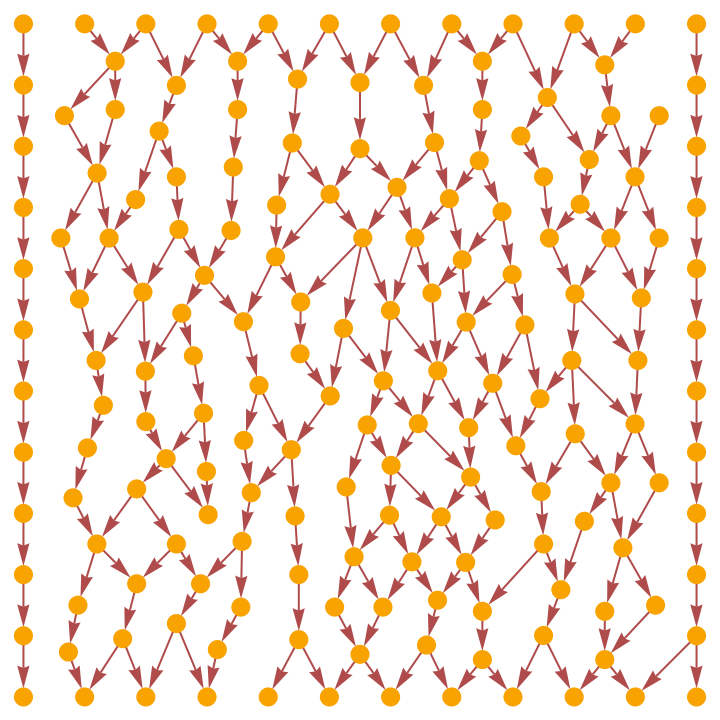
|
Plot the positions of the points in the triangulation only (without causal edges):
| In[27]:= |
|
| Out[27]= |

|
Show a complete list of spacetime coordinates for the points in the triangulation (the last coordinate is always the time coordinate):
| In[28]:= |
|
| Out[28]= |

|
Show the number of points in the triangulation:
| In[29]:= |
|
| Out[29]= |
|
Show the number of dimensions in the background spacetime:
| In[30]:= |
|
| Out[30]= |
|
Show the first 50 (undirected) edges in the triangulation of the spacetime surface:
| In[31]:= |
|
| Out[31]= |

|
Show the total number of (undirected) edges in the triangulation of the spacetime surface:
| In[32]:= |
|
| Out[32]= |
|
Show the maximum measure (in this case, area) of the simplices in the triangulation:
| In[33]:= |
|
| Out[33]= |
|
Show the total number of causal edges:
| In[34]:= |
|
| Out[34]= |
|
Show the number of causal edges after transitive reduction:
| In[35]:= |
|
| Out[35]= |
|
Show the total number of causal edges appearing in the triangulation:
| In[36]:= |
|
| Out[36]= |
|
Show the number of causal edges appearing in the triangulation after transitive reduction:
| In[37]:= |
|
| Out[37]= |
|
Show the pure full causal graph (with vertex coordinate information removed):
| In[38]:= |
|
| Out[38]= |
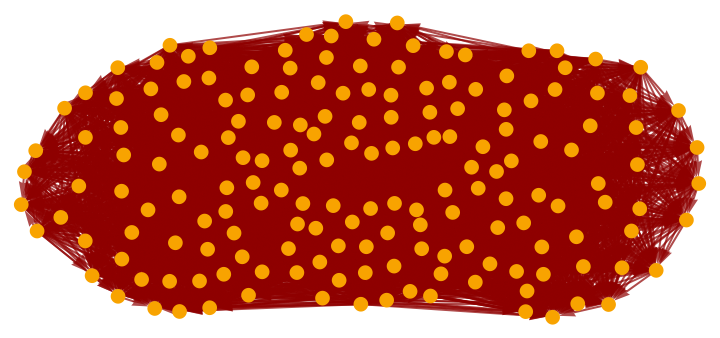
|
Show the pure transitively-reduced causal graph (with vertex coordinate information removed):
| In[39]:= |
|
| Out[39]= |

|
Show the pure full causal graph using only triangulation edges (with vertex coordinate information removed):
| In[40]:= |
|
| Out[40]= |
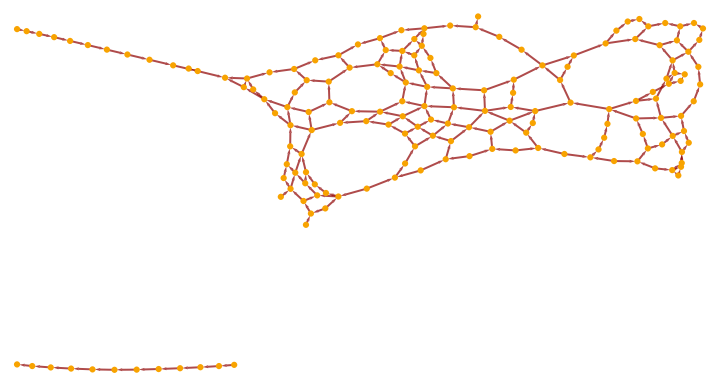
|
Show the pure transitively-reduced causal graph using only triangulation edges (with vertex coordinate information removed):
| In[41]:= |
|
| Out[41]= |
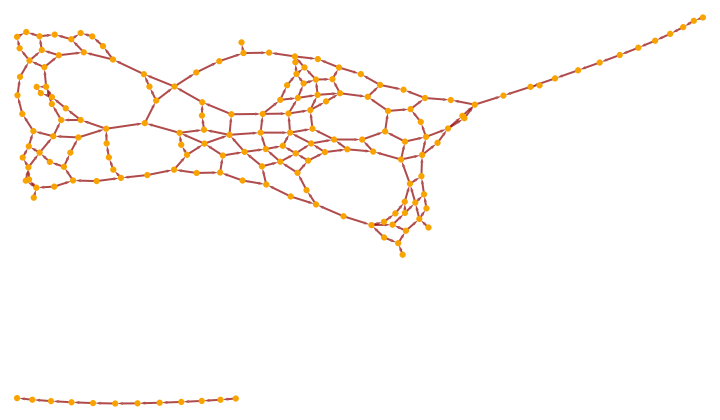
|
Show the mesh region corresponding to the triangulated spacetime surface:
| In[42]:= |
|
| Out[42]= |

|
Show the connectivity graph of this mesh region:
| In[43]:= |
|
| Out[43]= |

|
This work is licensed under a Creative Commons Attribution 4.0 International License