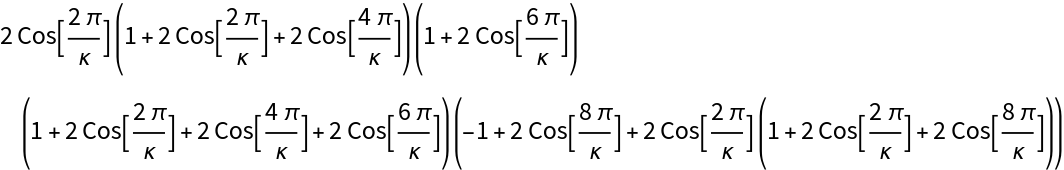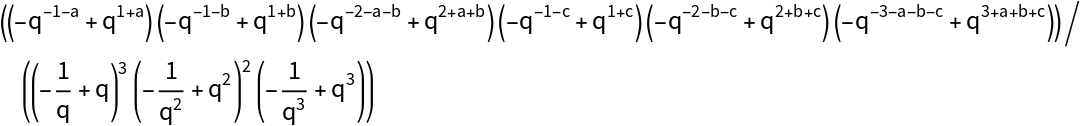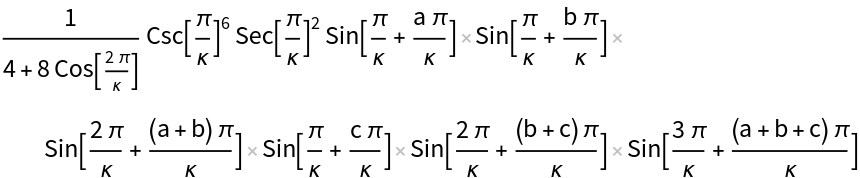Details
The Weyl dimension formula involves the product over all the positive
roots of the inner products between them and the highest weight shifted by the Weyl vector.
The collection of inner products entering the Weyl dimension formula can be encoded by labels attached to the vertices of the periodic quiver of roots.
For simply-laced Lie algebras (i.e., the ADE cases) the periodic quiver of roots is deduced from the adjacency matrix of the Dynkin diagram and from the matrices that describe the fusion algebra of SU(2) at an appropriate level. For non-simply-laced cases the calculation is similar but it involves specific scaling factors for the Coxeter orbits of short and long roots.
Standard notations for classical groups and their Lie algebras:
| Ar, r >= 1 | also called su(r+1), the Lie algebras of the special unitary groups |
| Dr, r >= 3 | also called so(2r), the Lie algebras of the special orthogonal groups (even case) |
| Br, r >= 2 | also called so(2r+1), the Lie algebras of the special orthogonal groups (odd case) |
| Cr, r >=2 | also called sp(r) or usp(2r), the Lie algebras of the (compact) symplectic groups |
| E6, E7, E8, G2, F4 | exceptional simple Lie groups. |
The argument string of the function ResourceFunction["LieIrrepDimension"] refers to one of the names that appears in the previous table, for instance "A5", "D10", "G2", or "E6".
The argument ruplet is the list of components of the highest weight in the basis of fundamental weights. It specifies the chosen irreducible representation. The components can be formal symbols, or non-negative integers.
The length of ruplet must match the rank of the chosen Lie algebra.
The ordering of fundamental weights in the list of components ruplet is determined by the ordering of vertices of the associated Dynkin diagram or by the list of simple roots.This ordering is standard (from left to right) for Ar. The two special simple roots of Dr are the last two. The special simple root in E6, E7, or E8, is the last one. Non simply-laced cases: For Br, the last root to the right is the unique short simple root. For G2, the short simple root is also to the right. For Cr, the short roots (all the simple roots but one) are to the left. For F4 there should be no ambiguity. The ordering can also be inferred from the dimensions of fundamental representations.
The input pattern
ResourceFunction["LieIrrepDimension"][
ruplet] assumes that the Lie algebra is of type Ar, in which case the dimension of an irreducible representation specified by the list
ruplet of components (
xj) is given by the following expression:
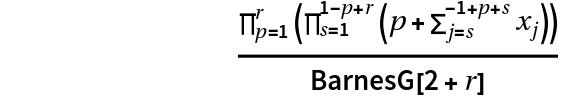
.
If one uses the pattern LieIrrepDimension["alg", ruplet, "Classical"], the function resource is calculated from the Weyl dimension formula by constructing the quiver of roots. In the Ar case, for any choice of the rank r, one has LieIrrepDimension["Ar", ruplet,"Classical"] = LieIrrepDimension[ruplet] but these two calls use different internal methods.
LieIrrepDimension["alg", ruplet, "Quantum",q] calculates the q-dimension (quantum dimension) and uses the same algorithm as in the classical case, but the inner products associated with the vertices of the periodic quiver of roots are calculated in terms of q-numbers.
The results obtained by calling DimensionIrrepLie["alg", ruplet, "Quantum",q], DimensionIrrepLie["alg", ruplet, "Quantum",q,Y], LieIrrepDimension["alg", ruplet, "Quantum",q,"QPoch"], or LieIrrepDimension["alg", ruplet, "Quantum",q,"()"], are mathematically equal, but formally distinct. One has Y[n,q] = Subscript[(n),q]= (q^n-q^(-n))/(q-q^(-1)).
The classical dimension (the usual dimension LieIrrepDimension["alg", ruplet,"Classical"]) is recovered from the quantum dimension LieIrrepDimension["alg", ruplet,"Quantum", q] when q goes to 1.
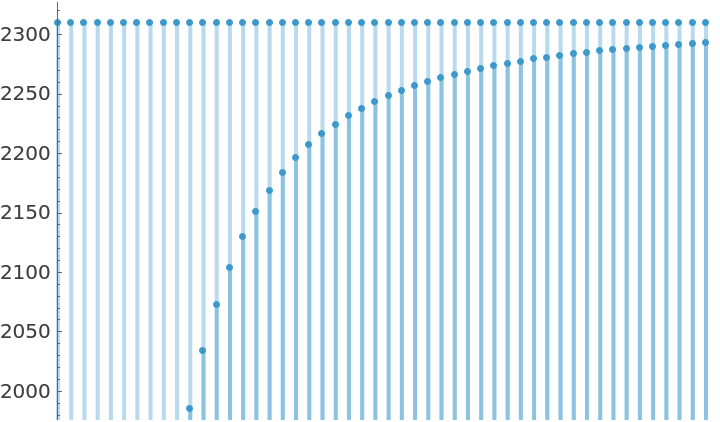
When q is a root of unity, namely q = Exp[I Pi/κ], with κ a non-negative integer, it is usually better to call LieIrrepDimension[string, ruplet, "RootOfUnity",κ] because the associated code tries to express the result as a simplified trigonometric expression (the simplification may be slow). For a given Lie algebra, the integer κ should be large enough for the chosen irrep specified by ruplet to exist (see an illustration of this phenomena in the section Applications).
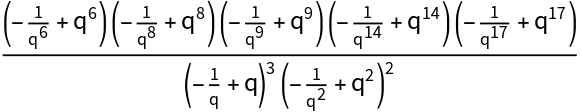
![]() :
:![]() :
:![(* Evaluate this cell to get the example input *) CloudGet["https://www.wolframcloud.com/obj/60f1ea8e-4c12-4e9b-8f7f-85098df2e62d"]](https://www.wolframcloud.com/obj/resourcesystem/images/d2c/d2cd8833-2137-48db-a319-a190d4d684f5/20bf58a4ddebefa6.png)
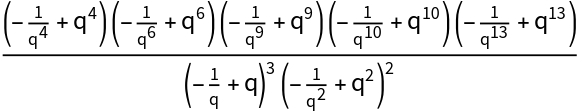
![]()
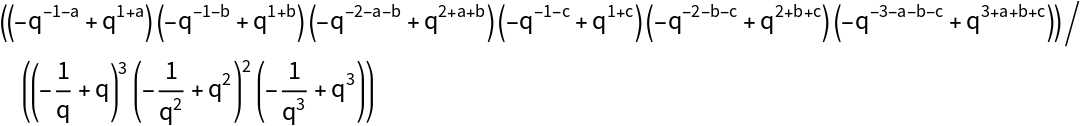
![Limit[ResourceFunction["LieIrrepDimension"]["A3", {a, b, c}, "Quantum",
q], q -> 1] == ResourceFunction["LieIrrepDimension"]["A3", {a, b, c}, "Classical"]](https://www.wolframcloud.com/obj/resourcesystem/images/d2c/d2cd8833-2137-48db-a319-a190d4d684f5/5a63d97baf59b1cb.png)
![ResourceFunction["LieIrrepDimension"] ["A2", {2, 5}, "RootOfUnity", \[Kappa]] == ResourceFunction["LieIrrepDimension"] ["A2", {2, 5}, "Quantum", Exp[I Pi/\[Kappa]]] // Simplify](https://www.wolframcloud.com/obj/resourcesystem/images/d2c/d2cd8833-2137-48db-a319-a190d4d684f5/750634d5d130cf71.png)
![Table[With[{r = rval}, ResourceFunction["LieIrrepDimension"][
Table[Subscript[x, j], {j, 1, r} ]] == \!\(
\*UnderoverscriptBox[\(\[Product]\), \(p = 1\), \(r\)]\((
\*UnderoverscriptBox[\(\[Product]\), \(s = 1\), \(1 - p + r\)]\((p +
\*UnderoverscriptBox[\(\[Sum]\), \(j = s\), \(\(-1\) + p + s\)]
\*SubscriptBox[\(x\), \(j\)])\))\)\)/BarnesG[2 + r]], {rval, 1, 7}]](https://www.wolframcloud.com/obj/resourcesystem/images/d2c/d2cd8833-2137-48db-a319-a190d4d684f5/4b7d750e6c8d357a.png)
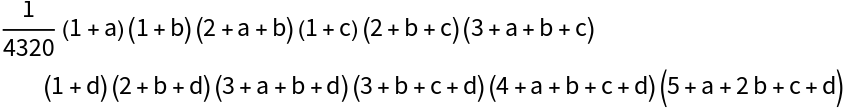
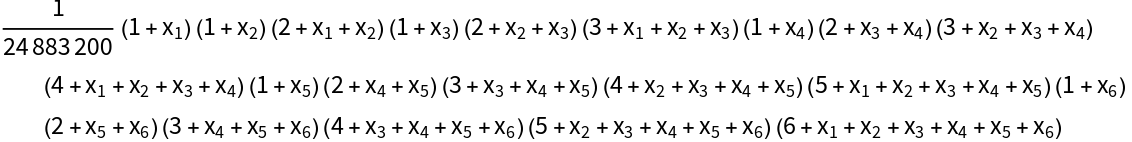
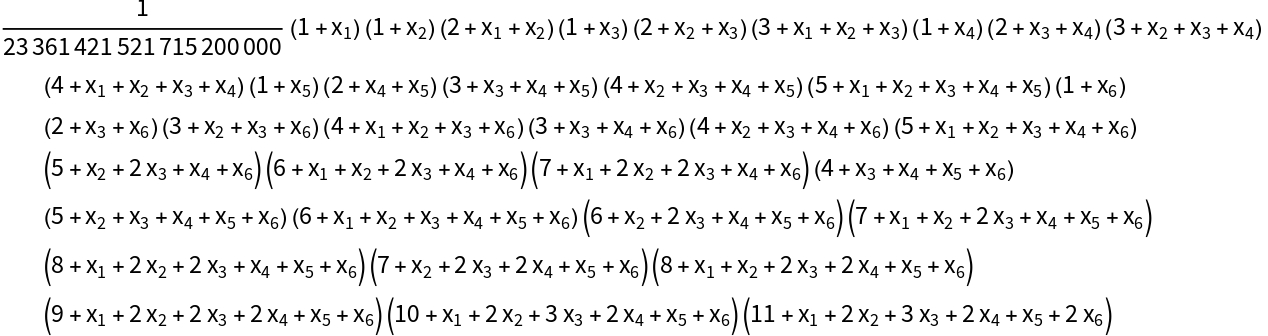
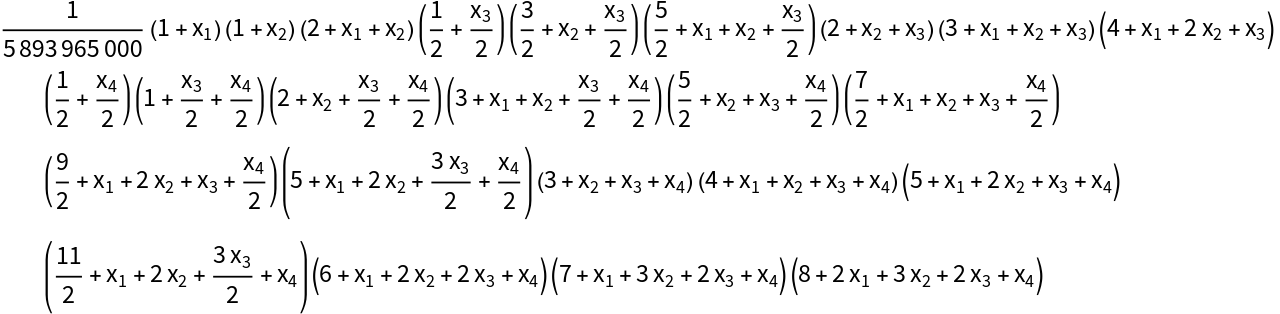
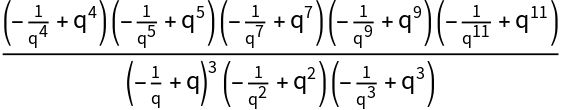
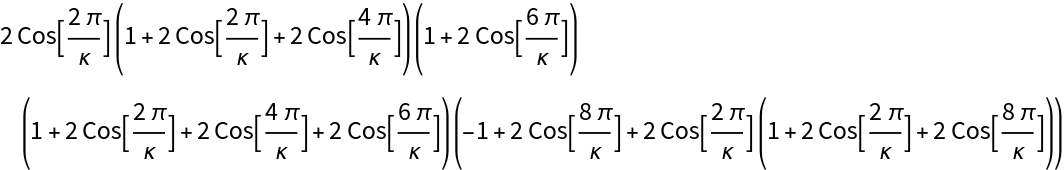
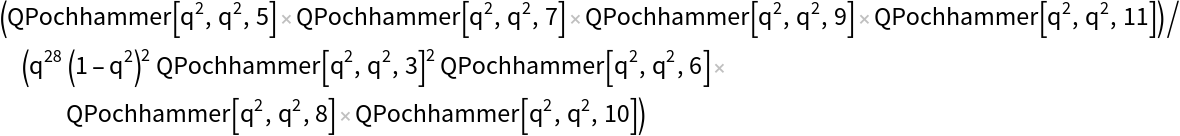
![integrableirrepsA[r_, k_] := Flatten[Apply[Table, Module[{a, li1 = Append[
Table[ToExpression[StringJoin[ToString[a], ToString[j]]], {j, r, 1, -1}], 0], li}, li = Prepend[li1, k]; Sequence[
Prepend[Table[{li[[j]], 0, li[[j - 1]]}, {j, 2, r + 1}], Drop[li1 - RotateLeft[li1], -1]]]]], r - 1]](https://www.wolframcloud.com/obj/resourcesystem/images/d2c/d2cd8833-2137-48db-a319-a190d4d684f5/475ab6960998ff23.png)