Details and Options
Given positive integers
a,b such that
a>b and a semiprime
N, we may compute a factor,
q, of
N by creating the sequence
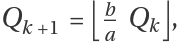
where
Q0=N. The sequence terminates if
Qk<2, in which case the method has failed for the
a/b-rational base representation. Otherwise, the sequence terminates if
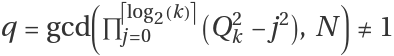
, in which case we have found a factor,
q, of
N.
Similar to Fermat's factorisation algorithm, which factors
N=p q quickly when
p is close to

,
ResourceFunction["FactorSemiprime"] will factor
N=p q quickly when
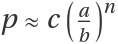
, with
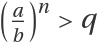
and
a,b are exhaustively searchable.
Similar to trial division, which tests successive odd integers for divisibility, ResourceFunction["FactorSemiprime"] exhaustively tests each possible a/b-rational base representation of p in lexicographic order. That is, a/b=2,3,4,3/2,5,6,5/2,4/3,7,5/3,…
However, unlike trial division, for a single
a/b, if
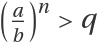
, then
ResourceFunction["FactorSemiprime"] will obtain the factor
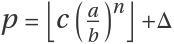
, for all
c∈ℕ and for all
Δ∈ℕ such that
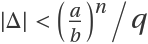
.
Much like other existing algorithms for integer factorisation, it is exceedingly unlikely that ResourceFunction["FactorSemiprime"] will quickly factor an arbitrary, large semiprime.
![ResourceFunction["FactorSemiprime"][
4035594397856978730116340001934921254572690987592701065254660135262792660067506541986580659177825246436531145839296242103812804324377528485848154088536008235413752938842227921141307849016281927942876956586098725341320205397768504290230954934143147130959878277148868527735858143934651684443466139855810555747255305233037482909186346108248405004315340601559] // RepeatedTiming](https://www.wolframcloud.com/obj/resourcesystem/images/d1b/d1b9a471-38b3-4f13-9efe-da5c7a75aa35/362d0299e168110a.png)

![SeedRandom[123456789];
q = RandomPrime[{2^131, 2^132}]
SeedRandom[];](https://www.wolframcloud.com/obj/resourcesystem/images/d1b/d1b9a471-38b3-4f13-9efe-da5c7a75aa35/5964ae3f33ee4595.png)
![p = NextPrime[(5/3)^555]
\[ScriptCapitalN] = p q
ResourceFunction["FactorSemiprime"][\[ScriptCapitalN]]](https://www.wolframcloud.com/obj/resourcesystem/images/d1b/d1b9a471-38b3-4f13-9efe-da5c7a75aa35/7299a54c623c8e9c.png)

![]() :
:![\[CapitalDelta] = Floor[(5/3)^555/q]
p = NextPrime[10001000100010003 (5/3)^555 - \[CapitalDelta]]
\[ScriptCapitalN]min = p q
ResourceFunction["FactorSemiprime"][\[ScriptCapitalN]min]](https://www.wolframcloud.com/obj/resourcesystem/images/d1b/d1b9a471-38b3-4f13-9efe-da5c7a75aa35/66e597ef6a7f7b42.png)

![\[CapitalDelta] = Floor[(5/3)^555/q]
p = NextPrime[10001000100010003 (5/3)^555 + \[CapitalDelta]]
\[ScriptCapitalN]max = p q
ResourceFunction["FactorSemiprime"][\[ScriptCapitalN]max]](https://www.wolframcloud.com/obj/resourcesystem/images/d1b/d1b9a471-38b3-4f13-9efe-da5c7a75aa35/7be593be1936ef00.png)

![ResourceFunction["FactorSemiprime"][
13070989587597546374716464770975785289589280708760293515652989663172886876841898461676231357599040014559104151905105163940698243537183737604630731215233980419718036692731072871532417578375227977581, "InitialBase" -> 278] // RepeatedTiming](https://www.wolframcloud.com/obj/resourcesystem/images/d1b/d1b9a471-38b3-4f13-9efe-da5c7a75aa35/581f320949e57ff2.png)
![ResourceFunction[
"FactorSemiprime"][2140324650240744961264423072839333563008614715144755017797754920881418023447140136643345519095804679610992851872470914587687396261921557363047454770520805119056493106687691590019759405693457452230589325976697471681738069364894699871578494975937497937, "SpecificBase" -> 913934318098202395814582302506729464949125254254317321565736649/
186798340046549841436465142394030629044917061492763974301888031]](https://www.wolframcloud.com/obj/resourcesystem/images/d1b/d1b9a471-38b3-4f13-9efe-da5c7a75aa35/3775b42b1af82e1b.png)
![NextPrime[100!]
NextPrime[334!]
% %% // ResourceFunction["FactorSemiprime"] // Timing](https://www.wolframcloud.com/obj/resourcesystem/images/d1b/d1b9a471-38b3-4f13-9efe-da5c7a75aa35/7651decdd5c41d0f.png)

