Function Repository Resource:

ListToCompleteBinaryTree

Convert a list into a complete binary tree

Contributed by: Shenghui Yang

ResourceFunction["ListToCompleteBinaryTree"][list]

arrange the elements from list row-wise in a binary tree which is complete except for the last row.

Details and Options

ListToCompleteBinaryTree returns a Tree object.

A binary tree is a hierarchical data structure in which each node has at most two children, referred to as the left child and the right child.

A complete binary tree (CBT) is a special type of binary tree where all the levels of the tree are filled completely except the lowest level nodes which are filled from as left as possible.

A CBT of height h has at least 2^h nodes and at most 2^h+1-1 nodes.

ListToCompleteBinaryTree accepts the same options as Tree.

Examples

Basic Examples (1)

Arrange 20 elements on a complete binary tree:

In[1]:=

Out[1]=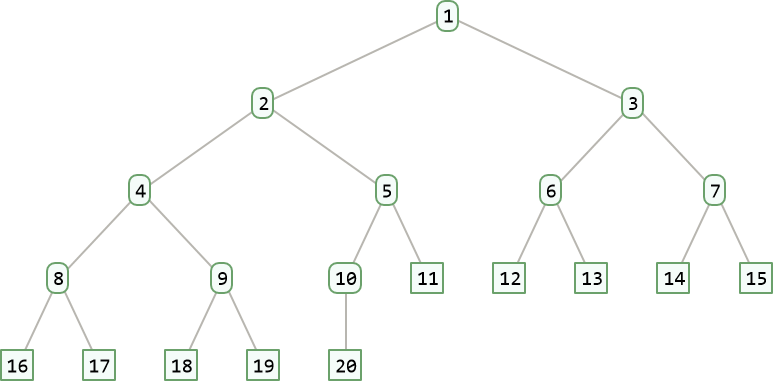

Options (2)

ListToBinaryTree accepts the same options as Tree:

In[2]:=

Out[2]=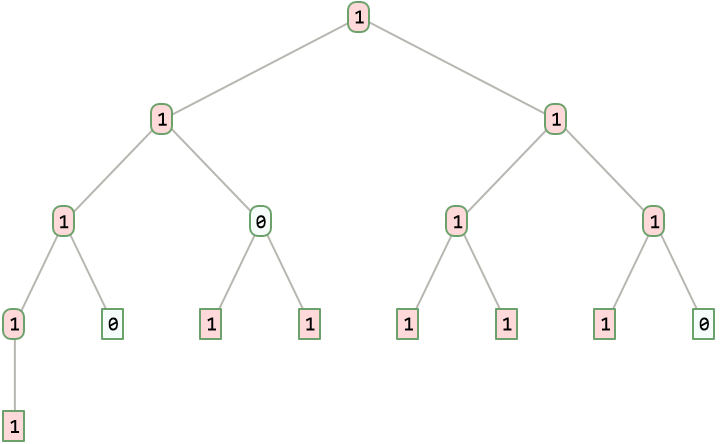

ListToBinaryTree accepts multiple options:

In[3]:=

ResourceFunction["ListToCompleteBinaryTree"][RandomInteger[{0, 1}, 36],
TreeElementShape -> All -> Graphics[{RGBColor["#101820"], Disk[{0, 1}, 1]}],
TreeElementSize -> All -> Scaled[0.12],
TreeElementLabelFunction -> All -> (Placed[
Style[#, 18, Bold, FontFamily -> "Courier", RGBColor["#F0EDCC"]],
Center] &)
]

Out[3]=

Properties and Relations (2)

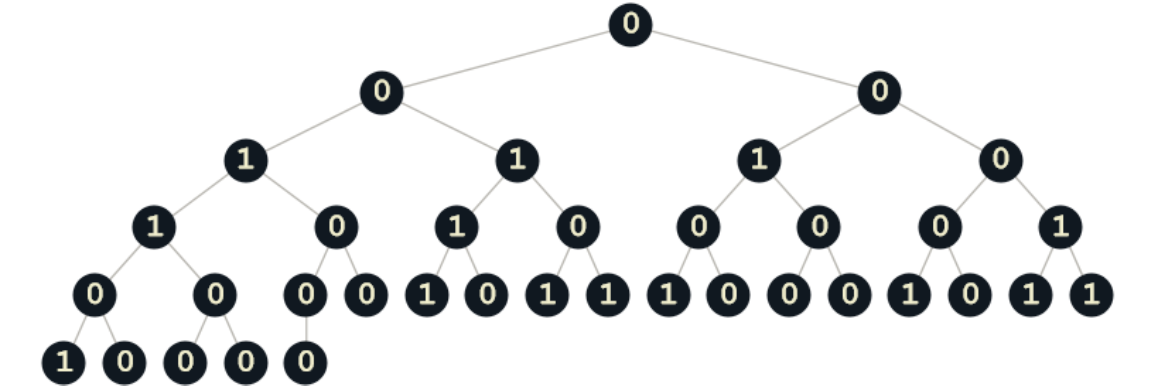A complete binary tree of height h has at least 2^h nodes and at most 2^h+1-1 nodes. For instance when h=4:

In[4]:=

Out[4]=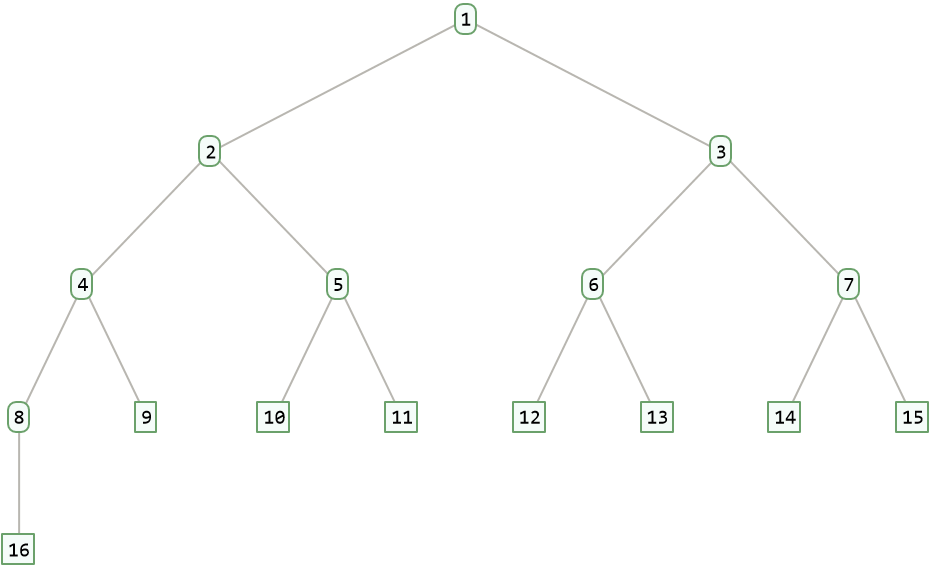

In[5]:=

Out[5]=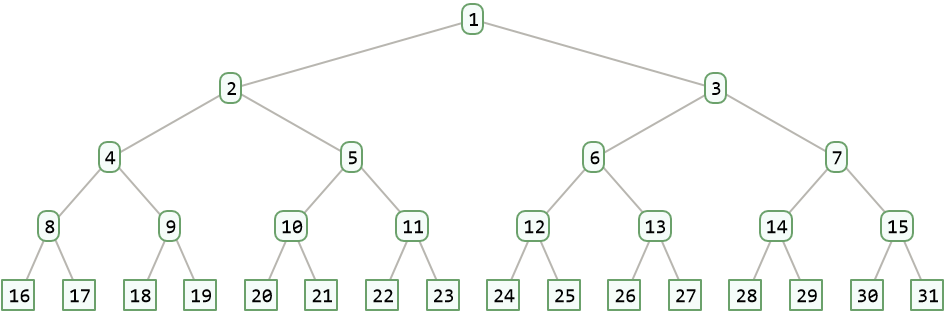

The height of the tree are the same for both complete binary trees:

In[6]:=

Out[6]=

A complete binary tree of 2^k-1 nodes is the same as complete Kary tree with (k-1) 2's:

In[7]:=

In[8]:=

Out[8]=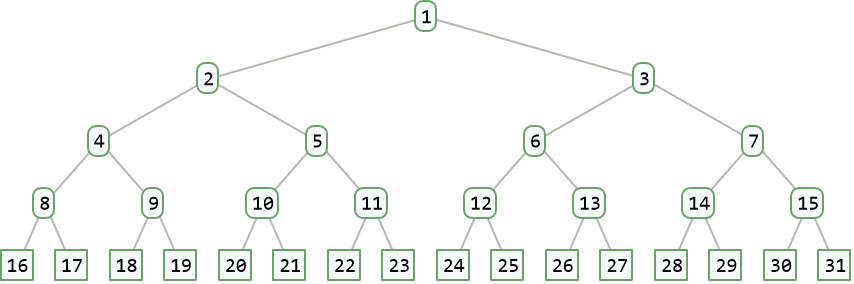

In[9]:=

Out[9]=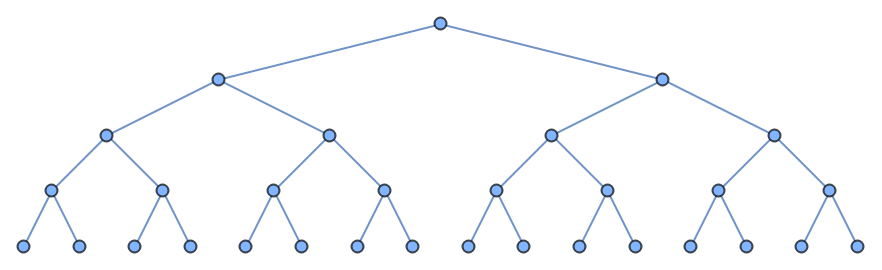

Possible Issues (1)

The length of the input must be at least one. Otherwise the function returns unevaluated:

In[10]:=

Out[10]=

Neat Examples (3)

Complete binary tree with 2ⁿ-1 nodes has beautiful "RadialEmbedding" configuration:

In[11]:=

Out[11]=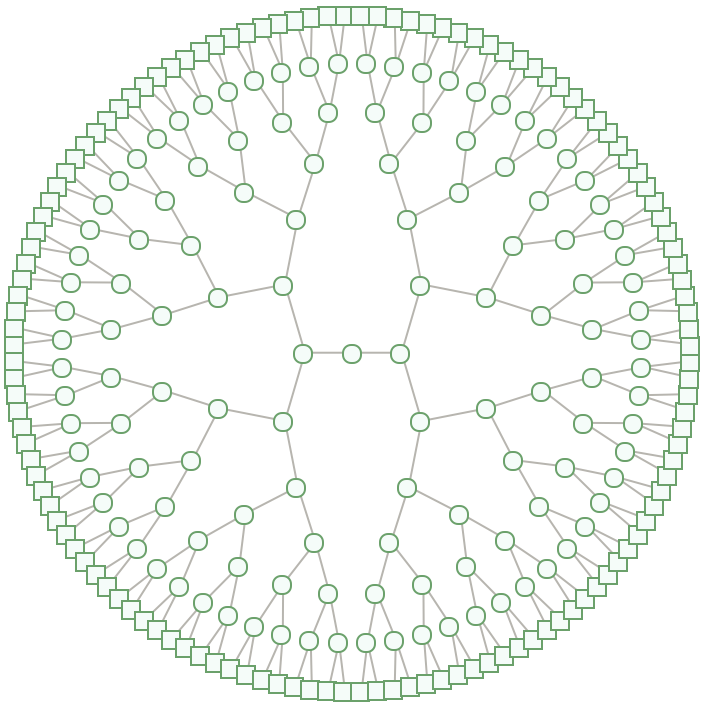

Use binary expansion of n as input to create a complete binary tree and then read those bits in pre-order (OEIS A380856):

In[12]:=

Out[12]=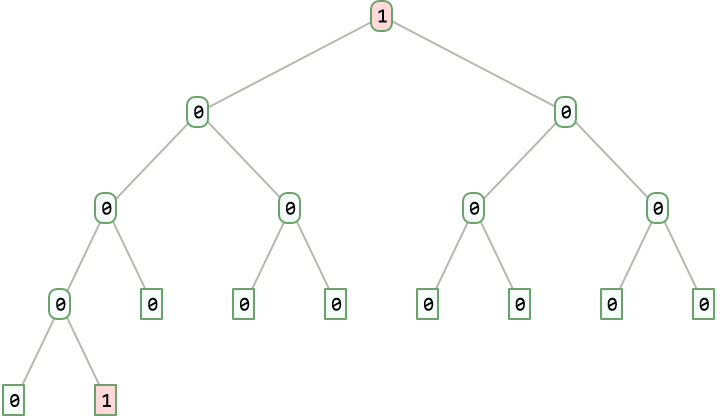

Specify TreeTraversalOrder to implement pre-order traversal:

In[13]:=

Out[13]=

The new number and its associated complete binary tree:

In[14]:=

Out[14]=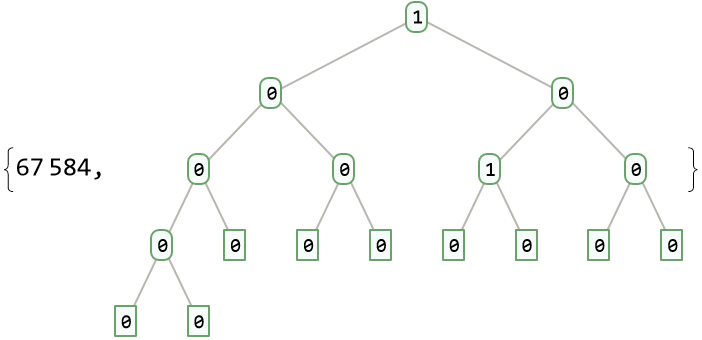

Every integer is associated with a permutation group using the operation from OEIS A380856:

In[15]:=

$permGroup[n_Integer] := Module[{bits, len, perm}, bits = IntegerDigits[n, 2]; len = Length[bits]; perm = Reap[TreeScan[Sow, ResourceFunction["ListToCompleteBinaryTree"][Range[len]], TreeTraversalOrder -> {"DepthFirst", "TopDown", "LeftRight"}]][[ 2, 1]]; PermutationGroup[{FindPermutation[perm]}] ]$