Basic Examples (2)
Expand a simple quadratic polynomial:
Expand a simple rational function:
Scope (5)
Complex-conjugate factorization of a real quadratic:
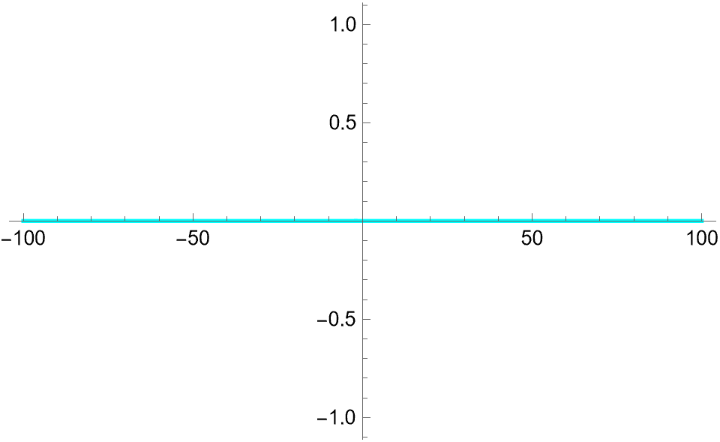
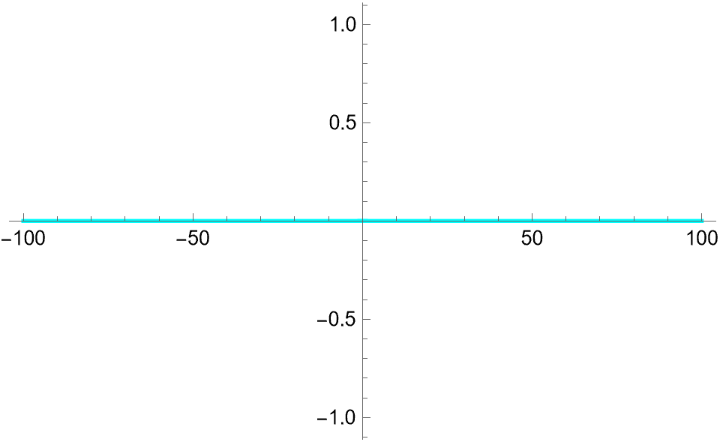
Verify that the expansion correctly represents the original function in the real line:
Branch-corrected expansion near a real root:
On the principal branch, when x>2 the factor 1-x/2 is negative real, each Log contributes πⅈ. LogAffineExpand automatically inserts a compensating piecewise constant term -2πⅈ so the result is exactly equal to the original input on the principal branch.
A similar branch correction for a simple rational function:
Expansion for a rational input - zeros minus poles, with sign and branch corrections:
Verify that the result is correct:
Root objects may appear in the result:
Use ToRadicals to express using radicals (may not work always):
Root objects in the expansion of a rational function:
Applications (3)
The canonical form of Log[polynomial] or Log[rational] is helpful for various symbolic and numeric computations.
Sum can compute faster with the affine expansion:
Integrate can compute faster with the affine expansion:
Conversion of a Log[polynomial] or Log[rational] expression to generalized polylogarithm form becomes straightforward through the affine expansion:
Properties and Relations (3)
PowerExpand applies identities like Log(ab)=Log(a)+Log(b) under generic assumptions and without managing branches, so it may stop at non-affine factors and either omit necessary 2πⅈ corrections or emit complex corrections:
LogAffineExpand always expands into affine factors and simplified 2πⅈ corrections:
Similarly for rational expressions:
Possible Issues (2)
For LogAffineExpand to work all constants appearing in the expression should be real and numeric. It won't work for symbolic or complex parameters:
LogAffineExpand gives an expansion which is guaranteed to be correct for real x only. It may not be valid for complex x:
Neat Examples (6)
Expansion of a high degree polynomial:
Builds a polynomial as ten times six factors. LogAffineExpand reduces its log to a constant plus one affine log per factor, inserting a piecewise 2πⅈ term for principal-branch correctness:
For a polynomial with repeated roots, the multiplicities reflect in the coefficients of the affine-log factors:
For real quadratics with negative discriminant, the two affine-log terms are complex conjugates. Their imaginary parts cancel for real x, so the result is purely real with no branch correction needed:
On rationals like (x^2-1)/(x-1)=1+x, the expansion cancels the common factor and reduces to Log[1+x] (up to the usual constant/branch bookkeeping):
For a random 3 x 3 integer matrix, LogAffineExpand rewrites Log[Det[I-xA]] as a constant plus one affine log per eigenvalue, adding a piecewise 2πⅈ term for principal-branch correctness on the real line. Nice for spectral checks and trace expansions:

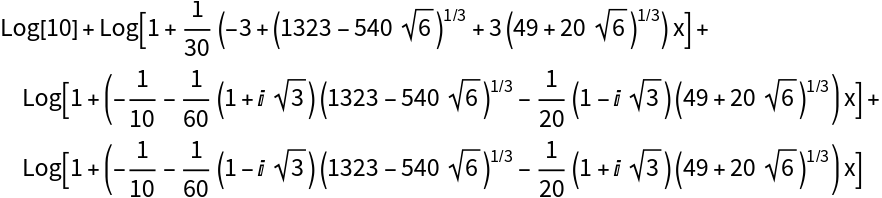

![AbsoluteTiming[
Sum[#, {x, 1, k}] & /@ ResourceFunction["LogAffineExpand"][
Log[(x^12 + 6 x^10 - 3 x + 10)/((x^2 - 2) (x^3 + 3 x + 1) (x^9 + 1))], x]][[1]]](https://www.wolframcloud.com/obj/resourcesystem/images/d0e/d0eb5e44-5a3e-439d-a7ca-590b34e84b3d/649bea2ada818883.png)
![AbsoluteTiming[
Integrate[#, x] & /@ ResourceFunction["LogAffineExpand"][
Log[(x^12 + 6 x^10 - 3 x + 10)/((x^2 - 2) (x^3 + 3 x + 1) (x^9 + 1))], x]][[1]]](https://www.wolframcloud.com/obj/resourcesystem/images/d0e/d0eb5e44-5a3e-439d-a7ca-590b34e84b3d/4b919b74889918ee.png)

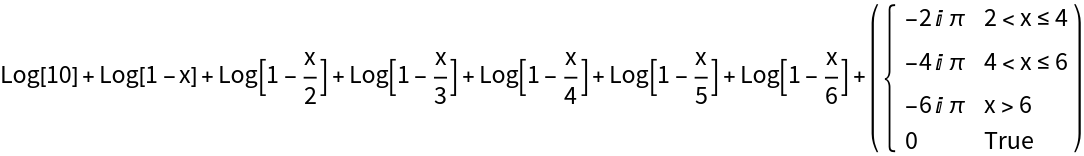
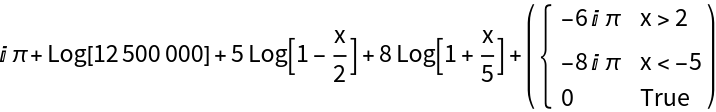
![SeedRandom[1];
A = RandomInteger[{-10, 10}, {3, 3}];
lam = Eigenvalues[A];](https://www.wolframcloud.com/obj/resourcesystem/images/d0e/d0eb5e44-5a3e-439d-a7ca-590b34e84b3d/0a03911dc6c8147e.png)