Wolfram Function Repository
Instant-use add-on functions for the Wolfram Language
Function Repository Resource:
Reach a goal number using given numbers and simple operands
ResourceFunction["KryptoGame"][numbers,goal] with basic operands, reach goal using all numbers. |
Reach a goal number of 11 with the values (2,3,5):
| In[1]:= |
| Out[1]= |
Reach a goal number of 11 with the values (2,3,5,8):
| In[2]:= |
| Out[2]= |
Compare to ResourceFunction Game24Solutions:
| In[3]:= |
| Out[3]= |
Reach a goal number of 16:
| In[4]:= |
| Out[4]= |
Convert the result to a computable form:
| In[5]:= |
| Out[5]= |
Reach a goal number of 7 with the values (2,5,8,13,21):
| In[6]:= |
| Out[6]= |  |
Some combinations are very tricky:
| In[7]:= |
| Out[7]= |
Repeated numbers are supported:
| In[8]:= |
| Out[8]= |
Some number sets reach the goal in many ways:
| In[9]:= |
| Out[9]= | 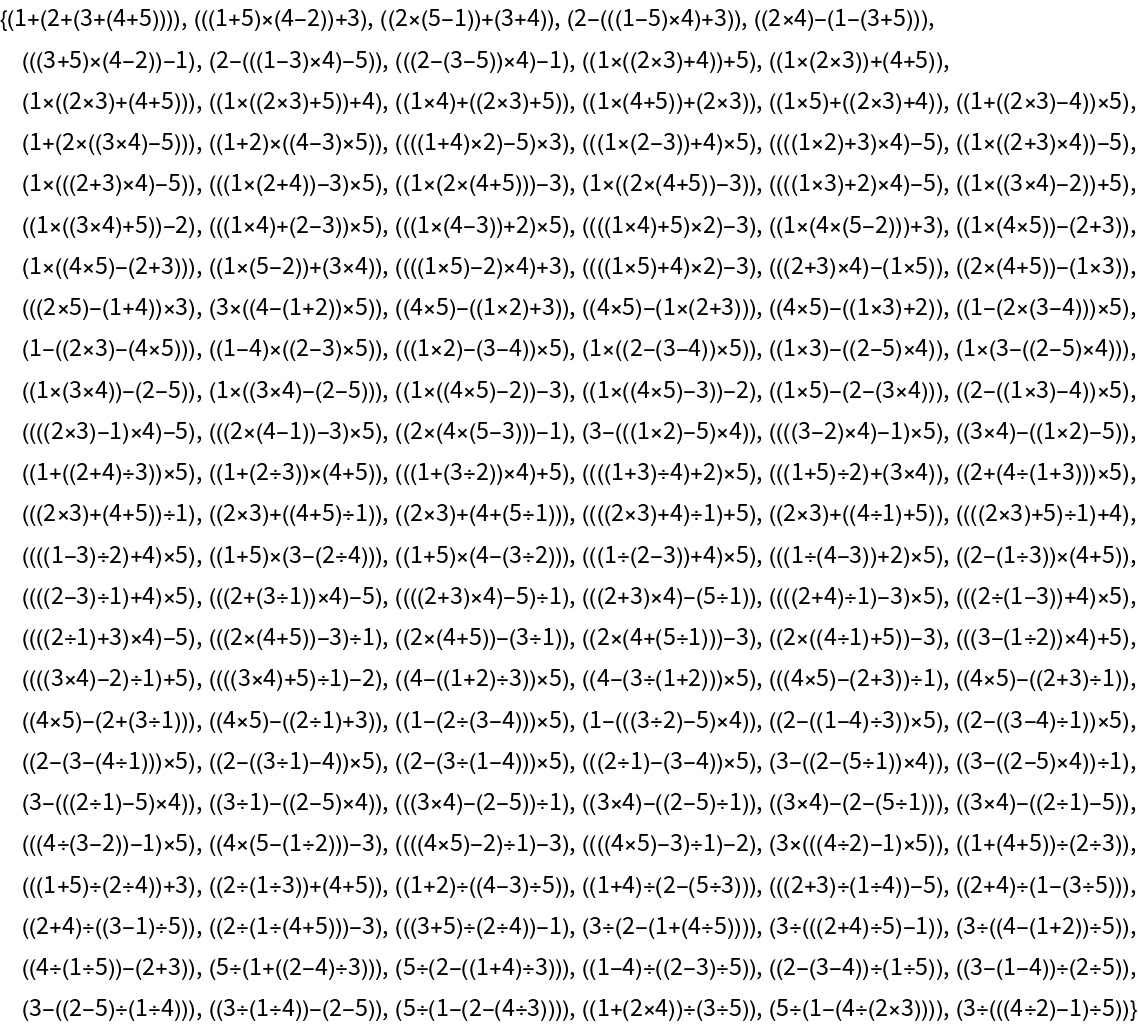 |
Only sets of 3, 4 or 5 numbers are allowed:
| In[10]:= |
| Out[10]= |
With three numbers, many goal numbers cannot be reached:
| In[11]:= |
| Out[11]= |  |
With four numbers, many more goal numbers can be reached:
| In[12]:= |
| Out[12]= | 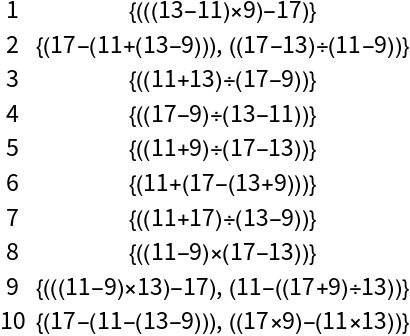 |
With five numbers, most goal numbers can be reached in many ways, but the solutions may be difficult:
| In[13]:= | ![Text@Grid[
Prepend[Table[
With[{res = ResourceFunction["KryptoGame"][{11, 17, 9, 13, 22}, k]}, {k, Length[res], First[res], Last[res]}], {k, 1, 10}], {"goal", "solutions", "simplest", "hardest"}], Frame -> All]](https://www.wolframcloud.com/obj/resourcesystem/images/d0c/d0ce04d1-1555-453e-a613-b6c60c91f0a2/18da0089a9c4461e.png) |
| Out[13]= |  |
A set of digits with ten unique solutions:
| In[14]:= |
| Out[14]= |  |
Wolfram Language 14.0 (January 2024) or above
This work is licensed under a Creative Commons Attribution 4.0 International License