Wolfram Function Repository
Instant-use add-on functions for the Wolfram Language
Function Repository Resource:
Create a pyritohedron
ResourceFunction["Pyritohedron"][h] returns a pyritohedron with displacement parameter h, represented as a Polyhedron object. |
A pyritohedron:
| In[1]:= |
|
| Out[1]= |

|
Surface area and volume of a pyritohedron:
| In[2]:= |
|
| Out[2]= |
|
Moment of inertia matrix for a pyritohedron:
| In[3]:= |
|
| Out[3]= |
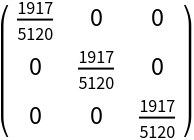
|
Pyritohedron[] is equivalent to Pyritohedron[1/2]:
| In[4]:= |
|
| Out[4]= |
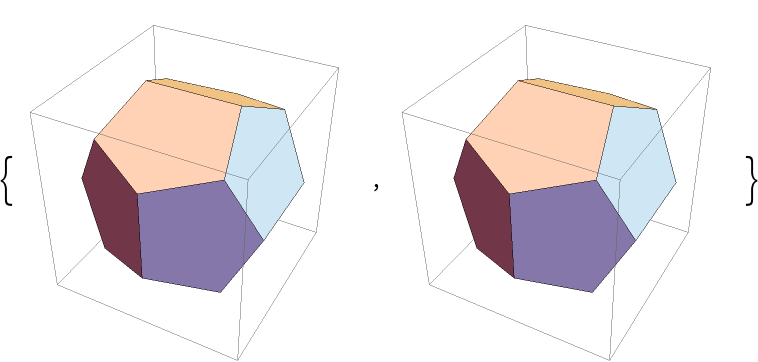
|
Pyritohedron[1/GoldenRatio] is equivalent to a regular dodecahedron:
| In[5]:= |
![{Graphics3D[ResourceFunction["Pyritohedron"][1/GoldenRatio]], Graphics3D[
Quiet@TransformedRegion[Dodecahedron[], AffineTransform[
EulerMatrix[{\[Pi]/2, -ArcCos[2/Sqrt[5] Sin[(2 \[Pi])/5]], 0}]/
GoldenRatio]]]}](https://www.wolframcloud.com/obj/resourcesystem/images/cdb/cdbc9b2e-0f8f-447b-85bb-703d39338fc6/0fa0efb1ff024b96.png)
|
| Out[5]= |
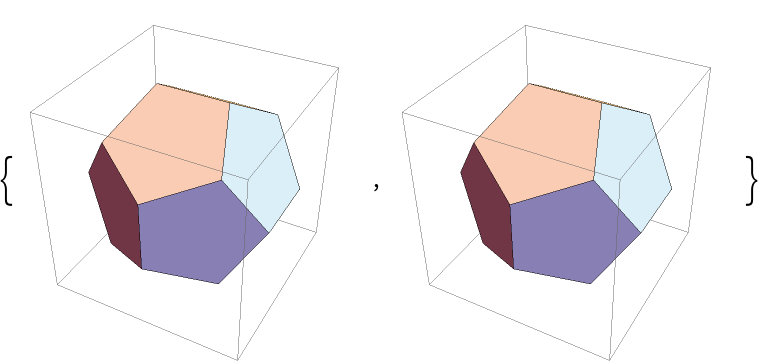
|
A pyritohedron is self-dual:
| In[6]:= |
![With[{h = 1/2}, Graphics3D[{ResourceFunction["Pyritohedron"][h], TransformedRegion[ResourceFunction["Pyritohedron"][h], RotationTransform[\[Pi]/2, {0, 0, 1}]]}]]](https://www.wolframcloud.com/obj/resourcesystem/images/cdb/cdbc9b2e-0f8f-447b-85bb-703d39338fc6/43c7be74012a2ca9.png)
|
| Out[6]= |

|
Show the effect of varying the displacement:
| In[7]:= |
|
| Out[7]= |
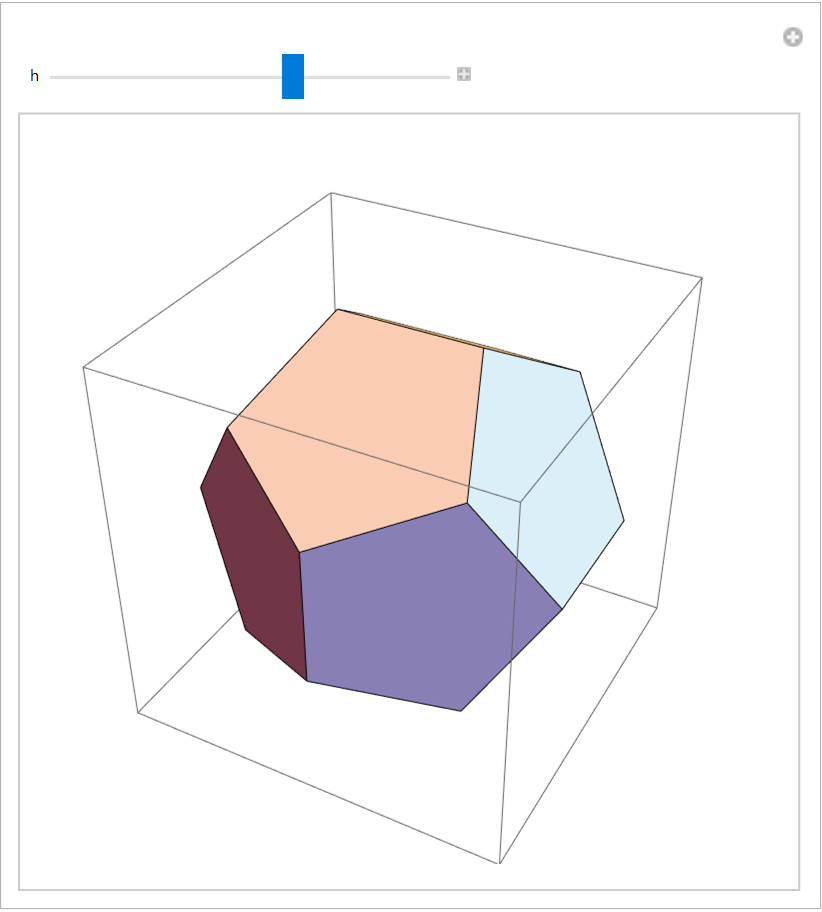
|
This work is licensed under a Creative Commons Attribution 4.0 International License