Basic Examples (2) 

Compute the pooled variance of two lists of data, one of which has three values and variance of 4, and the other of which has four values and a variance of 15:

In[1]:=

Out[1]=

Compute the pooled variance of symbolic data, assuming that the elements of the data are real:

In[2]:=

Out[2]=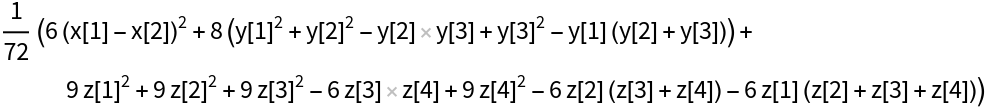

Scope (3) 

PooledVariance can work on collections of any finite length:

In[3]:=

Out[3]=

PooledVariance can work on complex values:

In[4]:=

Out[4]=

PooledVariance can work on symbolic values:

In[5]:=

Out[5]=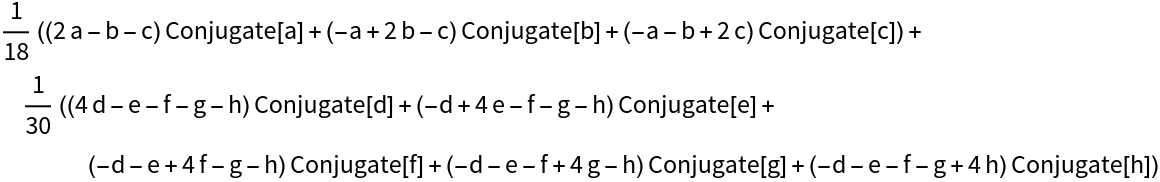

Applications (1) 

Compute Hedge’s g statistic, which makes use of the square root of a pooled variance to measure the effect size for the difference between means:

In[6]:=

Out[6]=

Properties and Relations (2) 

One can compute the pooled standard deviation by taking the square root of the pooled variance:

In[7]:=

Out[7]=

The same value can also be computed using the resource function PooledStandardDeviation:

In[8]:=

Out[8]=

The pooled variance of a collection is not the same as the variance of the flattened collection, even if the lengths of all the elements of the collection are the same:

In[9]:=

Out[9]=

Possible Issues (1) 

PooledVariance will not evaluate unless each inner list has a length greater than 1:

In[10]:=

Out[10]=