Wolfram Function Repository
Instant-use add-on functions for the Wolfram Language
Function Repository Resource:
Construct the intersection graph of intervals
ResourceFunction["IntervalGraph"][{interval1,interval2,…}] constructs the interval Graph defined by the intervali. |
The interval Graph of three intervals, two of which are overlapping:
| In[1]:= |
| Out[1]= |  |
Graphs returned by IntervalGraph are chordal and perfect:
| In[2]:= | ![ResourceFunction[
"IntervalGraph"][{Interval[{1, 6}], Interval[{2, 4}], Interval[{3, 11}], Interval[{5, 10}], Interval[{7, 8}], Interval[{9, 13}], Interval[{12, 14}]}, VertexLabels -> "Name", GraphLayout -> "CircularEmbedding"]](https://www.wolframcloud.com/obj/resourcesystem/images/caf/caf0e510-49b9-4c68-8da7-43c92f5f54a5/114609987a31d186.png) |
| Out[2]= | 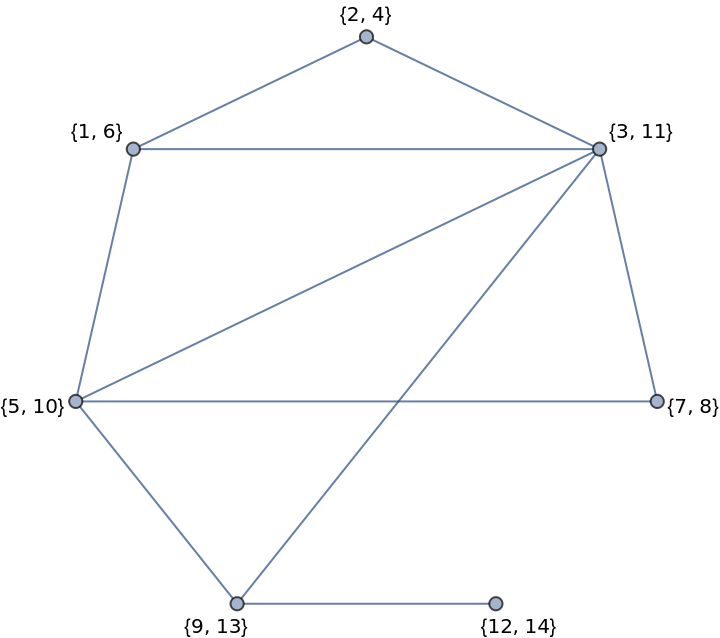 |
| In[3]:= |
| Out[3]= |
Star graphs can be constructed as interval graphs:
| In[4]:= |
| In[5]:= |
| Out[5]= | 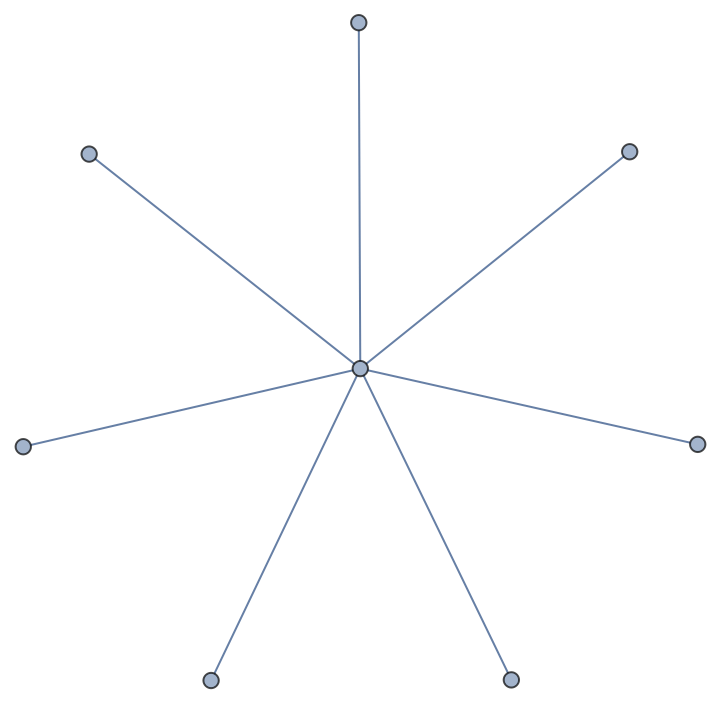 |
| In[6]:= |
| Out[6]= | 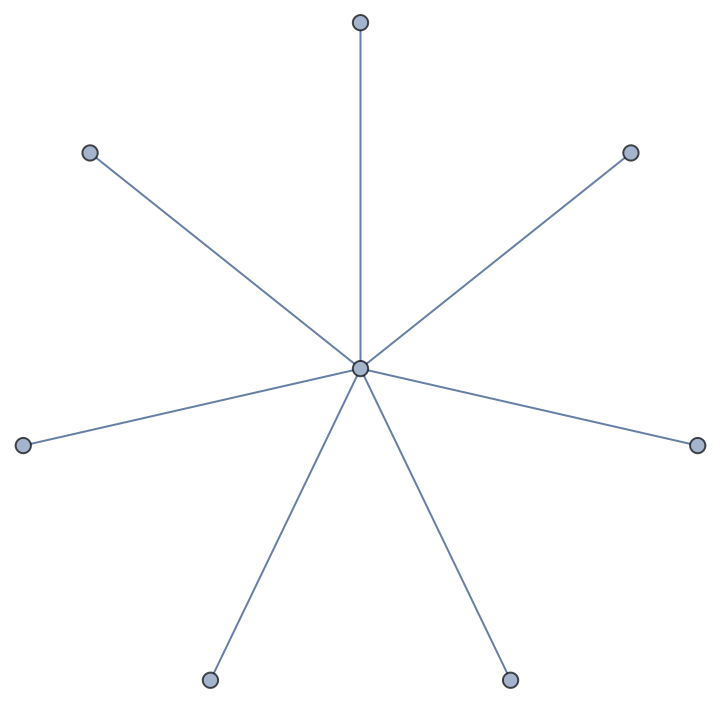 |
This work is licensed under a Creative Commons Attribution 4.0 International License