Wolfram Function Repository
Instant-use add-on functions for the Wolfram Language
Function Repository Resource:
Count the number of pairs of out-of-order elements in a permutation
ResourceFunction["InversionCount"][p] counts the number of inversions in permutation p. |
InversionCount gives the number of pairs of elements that must be reversed to bring the permutation to canonical order:
| In[1]:= |
| Out[1]= |
| In[2]:= |
| Out[2]= |
| In[3]:= |
| Out[3]= |
The number of inversions in a permutation of size n ranges from 0 to ![]() :
:
| In[4]:= |
| In[5]:= |
| Out[5]= |
| In[6]:= |
| Out[6]= |
The largest inversion count comes from the reverse of the identity permutation:
| In[7]:= |
| Out[7]= |
There are an average of n(n-l)/4 inversions per permutation:
| In[8]:= |
| In[9]:= |
| In[10]:= |
| Out[10]= |
| In[11]:= |
| In[12]:= |
| Out[12]= | 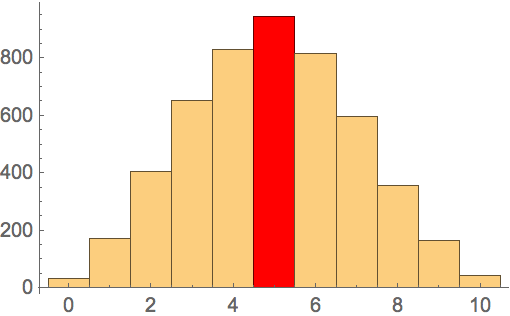 |
The number of inversions in a permutation is equal to that of its inverse:
| In[13]:= |
| Out[13]= |
| In[14]:= |
| Out[14]= |
The number of permutations of length n with major index k and inversion count i is the same as the number of permutations of length n with major index i and inversion count k:
| In[15]:= |
| In[16]:= |
| In[17]:= | ![Length[Select[
p, (ResourceFunction["PermutationMajorIndex"][#] == k && ResourceFunction["InversionCount"][#] == i) &]] === Length[Select[
p, (ResourceFunction["PermutationMajorIndex"][#] == i && ResourceFunction["InversionCount"][#] == k) &]]](https://www.wolframcloud.com/obj/resourcesystem/images/ca7/ca7aa9f9-58cf-419a-910c-14bc677fda29/56b53b31f86562de.png) |
| Out[17]= |
The number of inversions is a sum of elements of the inversion vector:
| In[18]:= |
| Out[18]= |
| In[19]:= |
| Out[19]= |
| In[20]:= |
| Out[20]= |
| In[21]:= |
| Out[21]= |
The number of inversions in a permutation is equal to the number of edges in its permutation graph:
| In[22]:= |
| Out[22]= |
| In[23]:= |
| Out[23]= |
The number of n permutations with k inversions is given by the resource function PermutationCountByInversions:
| In[24]:= |
| In[25]:= |
| Out[25]= |
| In[26]:= |
| Out[26]= |
| In[27]:= |
| Out[27]= |
This work is licensed under a Creative Commons Attribution 4.0 International License