Wolfram Function Repository

Instant-use add-on functions for the Wolfram Language

Function Repository Resource:

 VennGraphPlot

Source Notebook

Visualize the intersections of overlapping sets

Contributed by: Michael Sollami

ResourceFunction["VennGraphPlot"][{set1, set2, …}]

plots a graph showing the number of shared elements among the sets.

Details and Options

The graph visualizes the elements shared among the sets in what's also known as a Venn lattice.
ResourceFunction["VennGraphPlot"] takes the following options:
"Colors"Automaticcolors to use for the primary sets
GraphLayoutAutomaticthe embedding used in laying out the graph
"Labels"Automaticlabels to use for the sets
"Orders"Alldisplay the n–way intersections in the graph
"TooltipSamples"10the number of samples from each set to display in the tooltip
"TooltipRandomize"Truewhether to show random samples in tooltip

Examples

Basic Examples (3) 

Visualize the intersections of three sets:

In[1]:=
sets = {{"a", "b", "c"}, {"b"}, {"c"}};
In[2]:=
ResourceFunction["VennGraphPlot"][sets, "Labels" -> ToString /@ sets]
Out[2]=

Visualize the pairwise intersections of sets:

In[3]:=
s = Alphabet[][[;; #]] & /@ Range[5]
Out[3]=
In[4]:=
ResourceFunction["VennGraphPlot"][s, "Orders" -> 2]
Out[4]=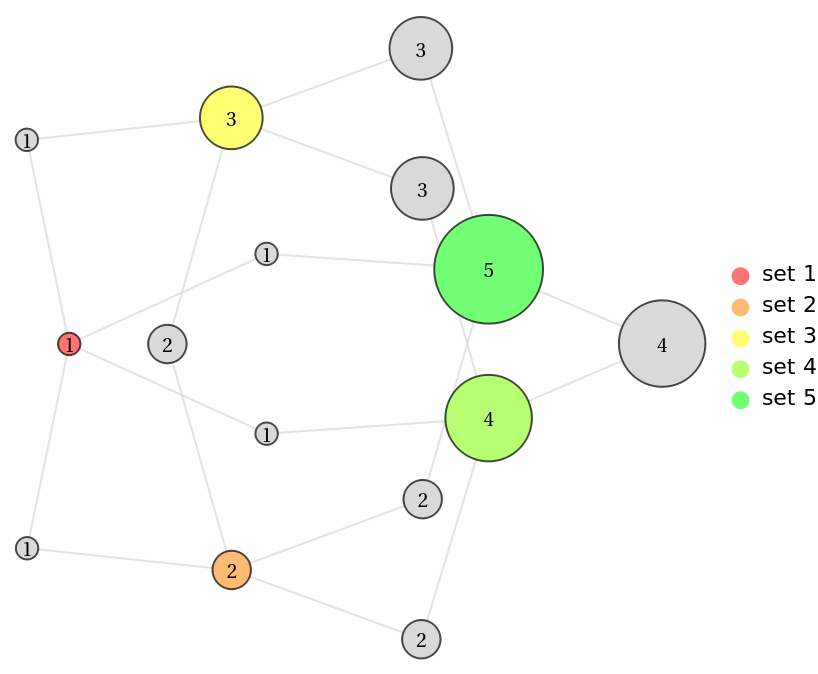

Plot a Venn graph with different intersection orders:

In[5]:=
sets = Range[1, 100, #] & /@ {5, 9, 15, 17, 4}; Manipulate[ ResourceFunction["VennGraphPlot"][sets, "Orders" -> order], {order, {2, 3, 4, 5, All}}]
Out[6]=

Options (2) 

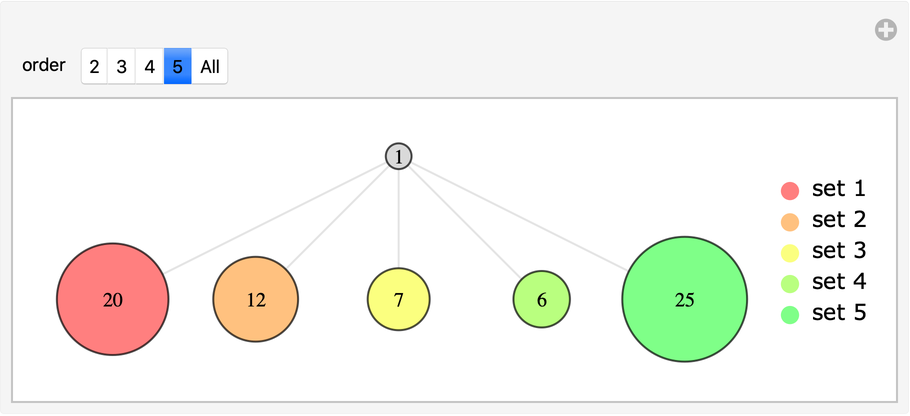You can change the colors used for the sets node with the "Colors" option:

In[7]:=
ResourceFunction[ "VennGraphPlot"][{{1, 2, 3, 4}, {2, 3, 4, 5}, {0, 1, 2, 3}}, "Colors" -> ResourceFunction["SampleColors"][104, 3]]
Out[7]=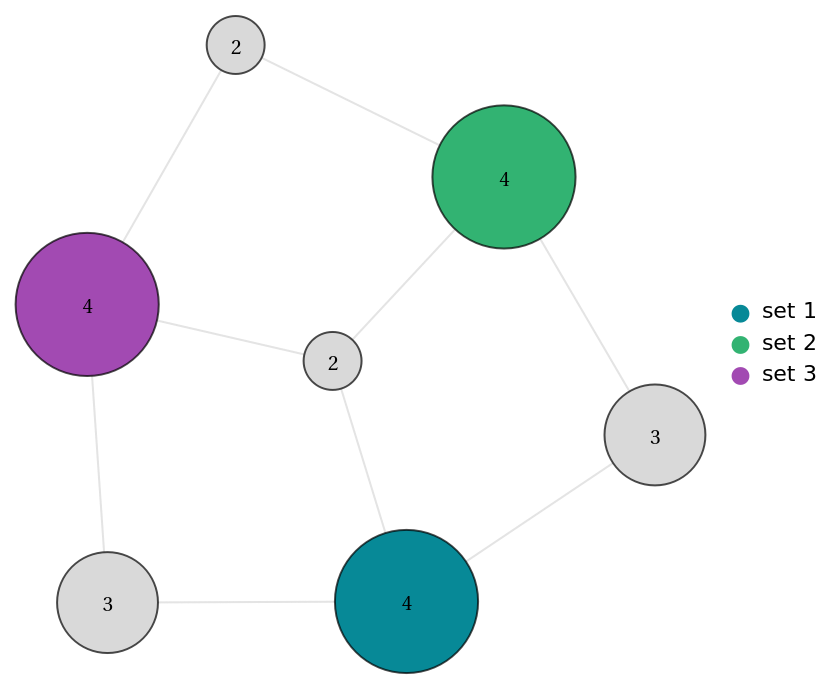

You can change the layout used with the GraphLayout option:

In[8]:=
ResourceFunction["VennGraphPlot"][s, GraphLayout -> "CircularEmbedding"]
Out[8]=

Applications (1) 

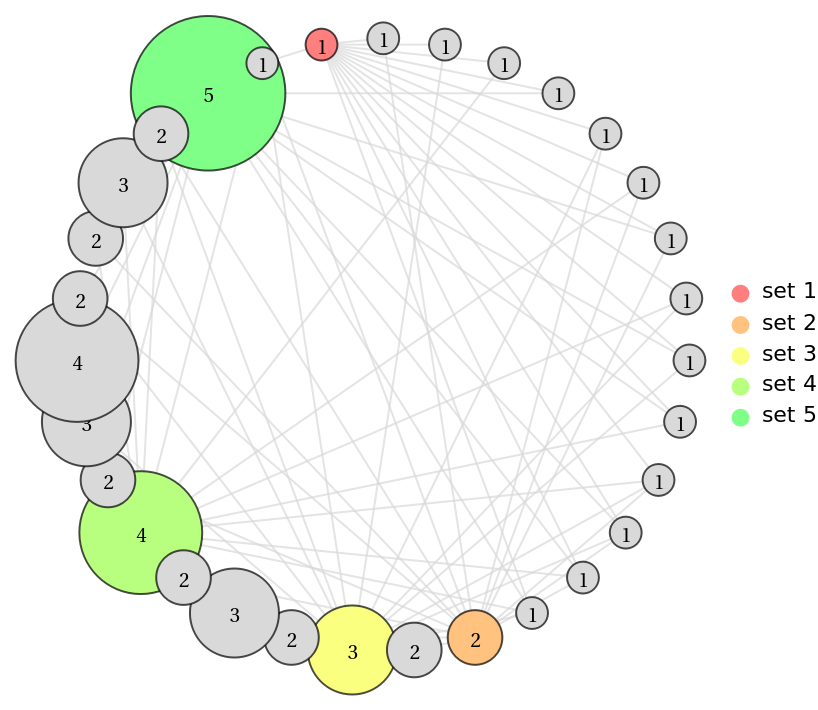Show the size of the shared memberships between four political blocs:

In[9]:=
cd = CountryData /@ {"FormerBritishColonies", "GroupOf8", "GroupOf15", "InternationalCriminalCourt"}; ResourceFunction["VennGraphPlot"][cd, "Labels" -> {"Colonies", "G8", "G15", "ICC"}]
Out[10]=

Possible Issues (2) 

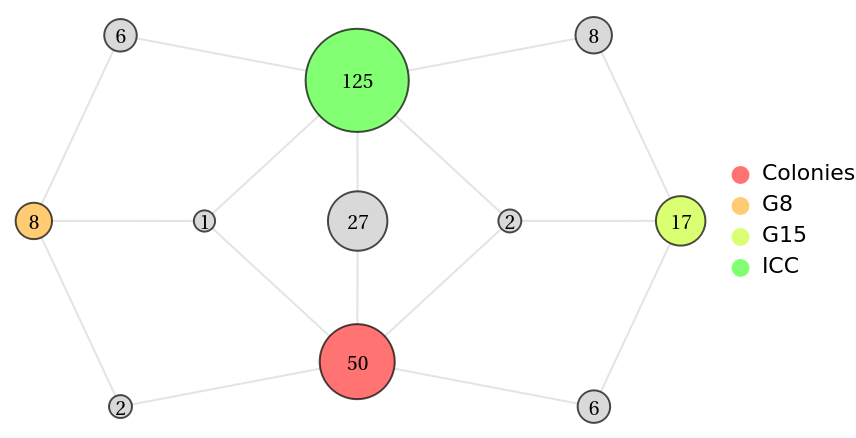There is no lattice for totally independent sets :

In[11]:=
ResourceFunction["VennGraphPlot"][{{1}, {2}, {3}}]
Out[11]=

The number of intersections can increase exponentially:

In[12]:=
ResourceFunction["VennGraphPlot"][Range /@ Range[10]]
Out[12]=

Publisher

Michael Sollami

Version History

  • 2.0.0 – 17 March 2020
  • 1.0.0 – 26 February 2020

Related Resources

License Information