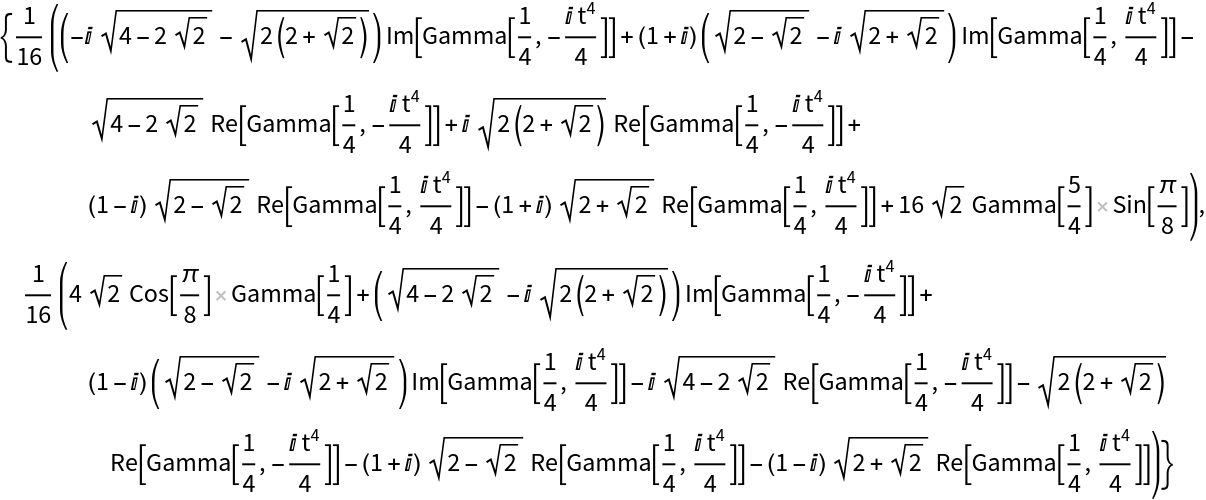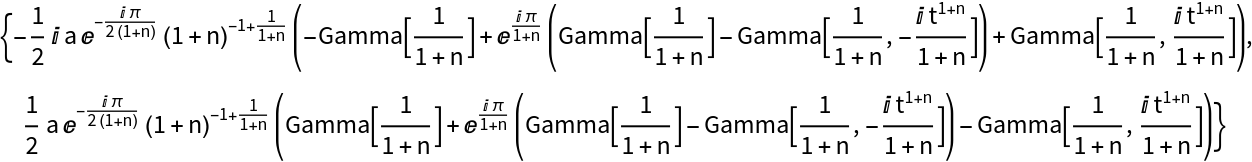Basic Examples (3)
Cesàro equation for the circle:
Cesàro equation for the logarithmic spiral:
Equations can be simplified using assumptions:
Cesàro equations for several curves:
Properties and Relations (2)
For some curves, entities can be used to get the Cesàro equation:
This can instead be computed by CesaroEquation with κ=1/ρ:
Cesàro equation for the Cornu spiral:
Curvature is linear:
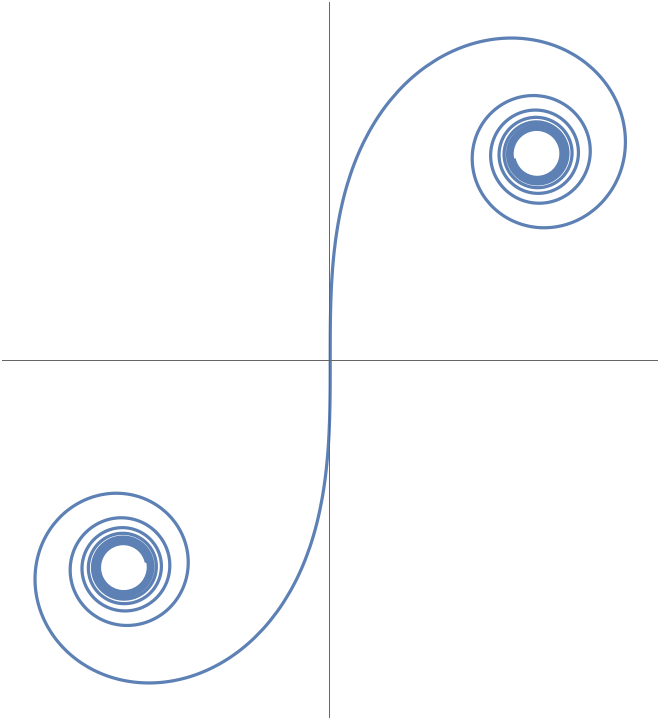
Alfred Gray’s generalization of the Cornu spiral:
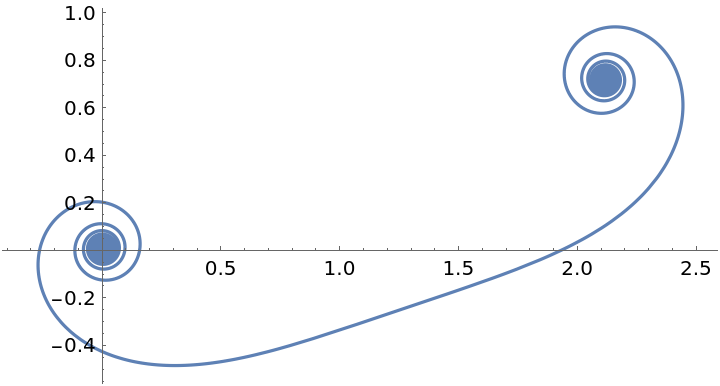
The clothoid for n, a both set to unity gives the Cornu spiral:
Plot the clothoid:
Different values give other types of special functions:
The clothoid for general values n, a:
Find the Cesàro equation for the clothoid:
The curvature takes the simpler form:
A plot of quadratic intrinsic curvature:
![ResourceFunction["CesaroEquation"][
Entity["PlaneCurve", "LogarithmicSpiral"]["ParametricEquations"][a, b][t], t, {\[Kappa], s}]](https://www.wolframcloud.com/obj/resourcesystem/images/c77/c77d9b1a-22cc-4552-92ee-6c22bb2a0ac4/3cc0eeae8c5cfc43.png)
![{#, ResourceFunction["CesaroEquation"][#["ParametricEquations"][a][t],
t, {\[Kappa], s}]} & /@ {Entity["PlaneCurve", "Catenary"], Entity["PlaneCurve", "CornuSpiral"], Entity["PlaneCurve", "CircleInvolute"], Entity["PlaneCurve", "Tractrix"], Entity["PlaneCurve", "Astroid"]} // FullSimplify // Grid](https://www.wolframcloud.com/obj/resourcesystem/images/c77/c77d9b1a-22cc-4552-92ee-6c22bb2a0ac4/468661bccd7c55f4.png)

![clothoidprime[n_, a_][t_] := {a Sin[t^(n + 1)/(n + 1)], a Cos[t^(n + 1)/(n + 1)]}
clothoid[n_, a_][s_] := Integrate[clothoidprime[n, a][ss], {ss, 0, s}, Assumptions -> t > 0 && n > 0]](https://www.wolframcloud.com/obj/resourcesystem/images/c77/c77d9b1a-22cc-4552-92ee-6c22bb2a0ac4/5f20b1052855848b.png)