Basic Examples (1) 

Test whether 100 can be expressed as a perfect power:

In[1]:=

Out[1]=

Scope (1) 

List of all perfect powers up to 10⁵:

In[2]:=

Out[2]=

Options (1) 

When a second argument k is passed, PerfectPowerQ checks whether n can be represented as the perfect k^th power of some integer greater than one:

In[3]:=

Out[3]=

Applications (1) 

The first few perfect powers without duplications are 1, 4, 8, 9, 16, 25, 27, 32, 36, 49, 64, 81, 100, 121, 125, … (OEIS A001597). Even more amazingly, the sum of the reciprocals of these numbers (excluding 1) is given by (OEIS A072102), where μ(k) is the Möbius function (MoebiusMu) and ζ(k) is the Riemann zeta function (Zeta).

This can be verified with the PerfectPowerQ function:

In[4]:=

In[5]:=

Out[5]=

Possible Issues (2) 

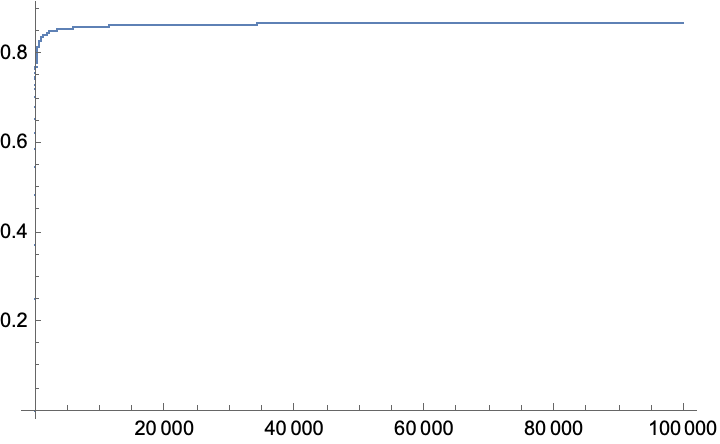The first argument should be an integer greater than 1:

In[6]:=

Out[6]=

The second argument, if given, should be greater than or equal to 2:

In[7]:=

Out[7]=

Properties and Relations (1) 

PerfectPowerQ of a prime number always yields False:

In[8]:=

Out[8]=