Wolfram Function Repository

Instant-use add-on functions for the Wolfram Language

Function Repository Resource:

 WenigerSum

Source Notebook

Evaluate an infinite sum using the Weniger transformation

Contributed by: Jan Mangaldan

ResourceFunction["WenigerSum"][f,{i,imin,∞}]

numerically evaluates the sum using the Weniger transformation.

Details and Options

Weniger's transformation is based on the evaluation of the expression , where Sn is the nth partial sum of the series, gn is an auxiliary sequence representing an error estimate of the infinite sum, (a)k is Pochhammer[a,k], and is DifferenceDelta[f,{i,n}].
The following options can be given:
"ExtraTerms"15number of terms to use in the Weniger transform
"Terms"15number of terms to sum directly
"Type"Automaticthe type of Weniger transformation to use
WorkingPrecisionMachinePrecisionthe precision used in internal computations
"Type" can be set to any one of the following types, corresponding to different Weniger transforms:
"T"t-transformation, gn=Sn-Sn-1
"U"u-transformation, gn=(n+1)(Sn-Sn-1)
"V"v-transformation, gn=-(Sn+1-Sn)(Sn-Sn-1)/(Sn+1-2Sn+Sn-1)
"D"d-transformation, gn=Sn+1-Sn
The t and d transformations work best with alternating series, while the u and v transformations are more flexible.
With sufficiently pathological summands, ResourceFunction["WenigerSum"] can give wrong answers. In most cases, you can test the answer by looking at its sensitivity to changes in the setting of options for ResourceFunction["WenigerSum"].
ResourceFunction["WenigerSum"] has attribute HoldAll, and effectively uses Block to localize variables.

Examples

Basic Examples (2) 

Evaluate the alternating harmonic series:

In[1]:=
ResourceFunction["WenigerSum"][(-1)^(j - 1)/j, {j, 1, \[Infinity]}]
Out[1]=

Compare with the closed form:

In[2]:=
% - Log[2]
Out[2]=

Options (8) 

ExtraTerms (2) 

Use 25 terms for the Weniger transformation:

In[3]:=
ResourceFunction["WenigerSum"][(-1)^k/(2 k + 1), {k, 0, \[Infinity]}, "ExtraTerms" -> 25, WorkingPrecision -> 25]
Out[3]=

Compare with the exact result:

In[4]:=
% - \[Pi]/4
Out[4]=

Set "Terms" to 0 so that all terms are used in extrapolation:

In[5]:=
ResourceFunction["WenigerSum"][(-1)^k/(2 k + 1), {k, 0, \[Infinity]}, "ExtraTerms" -> 25, "Terms" -> 0, WorkingPrecision -> 35]
Out[5]=

Compare with the exact result:

In[6]:=
% - \[Pi]/4
Out[6]=

Terms (2) 

Directly sum the first 25 terms before applying the Weniger transformation:

In[7]:=
ResourceFunction["WenigerSum"][(-1)^k/(2 k + 1), {k, 0, \[Infinity]}, "Terms" -> 25, WorkingPrecision -> 25]
Out[7]=

Compare with the exact result:

In[8]:=
% - \[Pi]/4
Out[8]=

Type (2) 

Show the results of the different Weniger transformations on an alternating series:

In[9]:=
TableForm[ Table[With[{r = ResourceFunction["WenigerSum"][(-1)^k/( 2 k + 1), {k, 0, \[Infinity]}, "Type" -> t, WorkingPrecision -> 25]}, {t, r, r - \[Pi]/4}], {t, {"T", "U", "V", "D"}}], TableHeadings -> {None, {"Type", "Result", "Error"}}]
Out[9]=

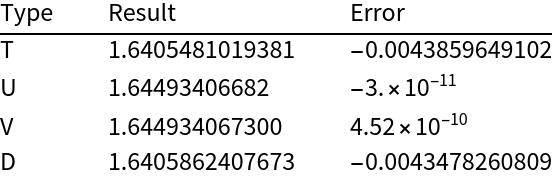
Show the results of the different Weniger transformations on a non-alternating series:

In[10]:=
TableForm[ Table[With[{r = ResourceFunction["WenigerSum"][1/k^2, {k, 1, \[Infinity]}, "Type" -> t, WorkingPrecision -> 25]}, {t, r, r - \[Pi]^2/6}], {t, {"T", "U", "V", "D"}}], TableHeadings -> {None, {"Type", "Result", "Error"}}]
Out[10]=

WorkingPrecision (2) 

Use a higher setting of WorkingPrecision:

In[11]:=
ResourceFunction["WenigerSum"][(-1)^k/(2 k + 1), {k, 0, \[Infinity]}, WorkingPrecision -> 25]
Out[11]=

Compare with the exact result:

In[12]:=
% - \[Pi]/4
Out[12]=

Applications (2) 

Use the Weniger d-transform to evaluate the Dirichlet eta function:

In[13]:=
eta[z_?NumericQ] := ResourceFunction["WenigerSum"][(-1)^(j - 1)/j^z, {j, 1, \[Infinity]}, "Type" -> "D"]

Compare with the built-in DirichletEta:

In[14]:=
Plot[{DirichletEta[z], eta[z]}, {z, -3, 3}, PlotStyle -> {Thick, Dashed}]
Out[14]=

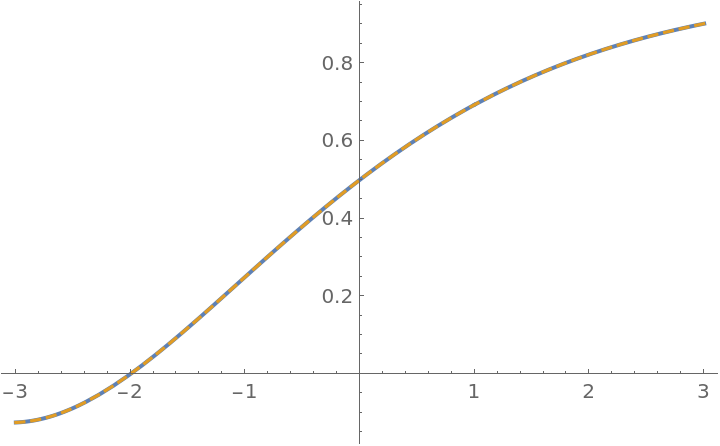
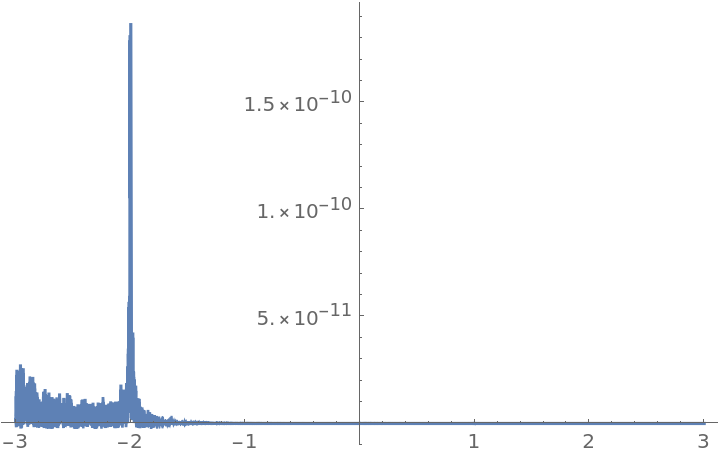
Plot the relative error:

In[15]:=
Plot[Abs[DirichletEta[z] - eta[z]]/Abs[DirichletEta[z]], {z, -3, 3}, PlotRange -> All]
Out[15]=

Use the Weniger v-transform with NIntegrate to numerically evaluate an oscillatory integral:

In[16]:=
term[j_Integer] := NIntegrate[ BesselJ[0, x], {x, BesselJZero[0, j], BesselJZero[0, j + 1]}, WorkingPrecision -> 25]
In[17]:=
NIntegrate[BesselJ[0, x], {x, 0, BesselJZero[0, 1]}, WorkingPrecision -> 25] + ResourceFunction["WenigerSum"][term[j], {j, 1, \[Infinity]}, "Type" -> "V", WorkingPrecision -> 25]
Out[17]=

Compare with the exact result:

In[18]:=
% - 1
Out[18]=

Properties and Relations (2) 

Directly summing the first few terms of a series usually does not give sufficient accuracy:

In[19]:=
Sum[N[(-1)^k/(2 k + 1), 35], {k, 0, 19}]
Out[19]=
In[20]:=
% - \[Pi]/4
Out[20]=

Using the Weniger transform on a series often gives better results:

In[21]:=
ResourceFunction["WenigerSum"][(-1)^k/(2 k + 1), {k, 0, \[Infinity]}, "ExtraTerms" -> 20, "Terms" -> 0, WorkingPrecision -> 35]
Out[21]=
In[22]:=
% - \[Pi]/4
Out[22]=

Possible Issues (2) 

WenigerSum may give finite results for formally divergent series:

In[23]:=
ResourceFunction["WenigerSum"][(-1)^j j!, {j, 0, \[Infinity]}, "Terms" -> 0, WorkingPrecision -> 25]
Out[23]=

Compare with the exact result:

In[24]:=
% - E ExpIntegralE[1, 1]
Out[24]=

Neat Examples (2) 

Numerically evaluate a formally divergent oscillatory integral:

In[25]:=
est = ResourceFunction["WenigerSum"][ NIntegrate[Sin[x] Log[x], {x, j \[Pi], (j + 1) \[Pi]}, WorkingPrecision -> 25], {j, 0, \[Infinity]}, "Type" -> "D", WorkingPrecision -> 25] // Quiet
Out[25]=

Compare with the exact answer:

In[26]:=
ex = Limit[\!\( \*SubsuperscriptBox[\(\[Integral]\), \(0\), \(\[Infinity]\)]\( \*SuperscriptBox[\(E\), \(\(-\[CurlyEpsilon]\)\ x\)] Sin[x] Log[ x] \[DifferentialD]x\)\), \[CurlyEpsilon] -> 0, Direction -> "FromAbove"]
Out[26]=
In[27]:=
est - ex
Out[27]=

Version History

  • 1.0.0 – 22 April 2021

Source Metadata

  • Citation:
    • Brezinski C., Redivo Zaglia M., Extrapolation Methods. Theory and Practice. Studies in Computational Mathematics, Vol. 2. Amsterdam: North-Holland Publishing Co., 1991.
      Available from https://www.sciencedirect.com/bookseries/studies-in-computational-mathematics/vol/2/suppl/C
    • Weniger E.J., Nonlinear sequence transformations for the acceleration of convergence and the summation of divergent series. Computer Physics Reports, vol. 10, 189-371, 1989.
      DOI: 10.1016/0167-7977(89)90011-7

Related Resources

License Information