Wolfram Function Repository
Instant-use add-on functions for the Wolfram Language
Function Repository Resource:
Compute the curve of aberrancy of a plane curve
ResourceFunction["AberrancyCurve"][c,t] computes the curve of aberrancy of the plane curve c parametrized by variable t. |
Define the parametric equations for an astroid:
| In[1]:= |
Compute its curve of aberrancy:
| In[2]:= |
| Out[2]= |
Plot the astroid and its curve of aberrancy:
| In[3]:= | ![\[Alpha] = astroid[1, t];
\[Delta] = Simplify[ResourceFunction["AberrancyCurve"][astroid[1, t], t]];
ParametricPlot[Evaluate[{\[Alpha], \[Delta]}], {t, -3, 3}]](https://www.wolframcloud.com/obj/resourcesystem/images/bd0/bd08622d-f880-46e0-aa78-5f4212ff4121/2b5e91ee48094cfe.png) |
| Out[3]= | 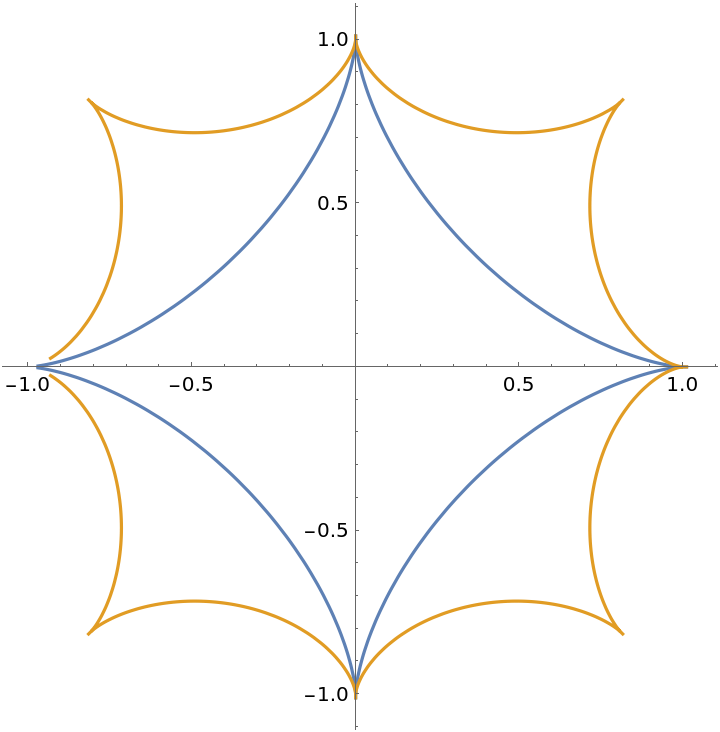 |
Compute the implicit equation for the curve of aberrancy of a quartic:
| In[4]:= |
| Out[4]= |
The curve of aberrancy of a plane curve involves third and fourth derivatives:
| In[5]:= |
| Out[5]= |
This work is licensed under a Creative Commons Attribution 4.0 International License