Wolfram Function Repository
Instant-use add-on functions for the Wolfram Language
Function Repository Resource:
Recognize functions by their power series expansions
ResourceFunction["RecognizeSeries"][series] attemps to find a function that generates the given power series. |
Recognize power series:
| In[1]:= |
|
| Out[1]= |
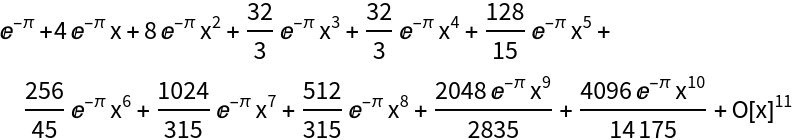
|
| In[2]:= |
|
| Out[2]= |
|
Recognize partial sums of series expansions:
| In[3]:= |
|
| Out[3]= |
|
| In[4]:= |
|
| Out[4]= |
|
| In[5]:= |
|
| Out[5]= |
|
Recognize products of functions:
| In[6]:= |
|
| Out[6]= |
|
| In[7]:= |
|
| Out[7]= |
|
| In[8]:= |
|
| Out[8]= |
|
| In[9]:= |
|
| Out[9]= |
|
Recognize sums and differences:
| In[10]:= |
|
| Out[10]= |
|
| In[11]:= |
|
| Out[11]= |
|
| In[12]:= |
|
| Out[12]= |
|
More complicated functions take longer:
| In[13]:= |
|
| Out[13]= |
|
RecognizeSeries may return generators in unsimplified forms:
| In[14]:= |
|
| Out[14]= |
|
| In[15]:= |
|
| Out[15]= |
|
This work is licensed under a Creative Commons Attribution 4.0 International License