Function Repository Resource:

TableWhile

Source Notebook

Create tables of values while given criteria hold

Contributed by: Lukas Lang

ResourceFunction["TableWhile"][expr,{i,start,condition}]

creates a table of expr with i running from start until condition[expr] no longer returns True.

ResourceFunction["TableWhile"][expr,{i,condition}]

creates a table of expr with i starting at 1.

ResourceFunction["TableWhile"][expr,{i,start,condition,step}]

increments i in increments of step.

ResourceFunction["TableWhile"][expr,condition]

creates a list of expr until condition[expr] no longer returns True.

ResourceFunction["TableWhile"][expr,{i,…},{j,…},…]

uses multiple iterators, each with its own condition.

ResourceFunction["TableWhile"][expr,{i,…,{end,condition},…}]

stops either when i reaches end or when condition[expr] no longer returns True.

ResourceFunction["TableWhile"][expr,{i,…,{condition,listCondition},…}]

continues while both condition[expr] and listCondition[{expr₁,expr₂,…}] return True.

ResourceFunction["TableWhile"][expr,{i,…,{end,condition,listCondition},…]

continues until i reaches end or either of the conditions fail.

ResourceFunction["TableWhile"][expr,{i,{i₁,i₂,…}},…]

uses successive values i₁,i₂,….

ResourceFunction["TableWhile"][expr,{i,{i₁,i₂,…},conditions},…]

stops iterations when the conditions first fail.

Details and Options

ResourceFunction["TableWhile"] works like Table, but supports conditions as criteria for termination.

ResourceFunction["TableWhile"] supports an extended version of the standard iterator specification:

{i,end}

run i from 1 to end in increments of 1

{i,start,end}

start from start

{i,start,end,step}

use increments of step

{i,{i₁,i₂,…}}

use successive values i₁,i₂,…

{i,{i₁,i₂,…},conditions}

only continue as long as condition is met

In all iterator specifications, end can be one of the following:

stop when the iteration variable reaches n

condition

stop when condition[expr] no longer returns True

{condition,listCondition}

also stop when listCondition[{expr₁,expr₂,…}] no longer returns True

{None, listCondition}

use only listCondition

{n, …}

also stop when the iteration variable reaches n

ResourceFunction["TableWhile"] uses NumericQ to distinguish between iteration bounds and conditions. This means that unlike for Table, symbolic iteration boundaries are not supported.

In the iterator specification {i,{i₁,i₂,…},conditions}, conditions can be either a single condition or a pair {condition,listCondition}.

In ResourceFunction["TableWhile"][expr,{…,condition,…}], condition is applied to each expression of the resulting list.

In ResourceFunction["TableWhile"][expr,{…,{…,listCondition},…}], listCondition is applied to the list of expressions generated so far at each step.

ResourceFunction["TableWhile"] terminates when either of condition[…] or listCondition[…] does not give True.

When condition[expr] in ResourceFunction["TableWhile"][expr,{i,…,condition,…}] is evaluated, the value of i of the current iteration can also be accessed. The same is true for evaluations of listCondition[{expr₁,expr₂,…}].

ResourceFunction["TableWhile"][expr,spec₁,spec₂] is effectively equivalent to ResourceFunction["TableWhile"][ResourceFunction["TableWhile"][expr,spec₂],spec₁].

ResourceFunction["TableWhile"] effectively uses Block to localize iterator variables.

ResourceFunction["TableWhile"] accepts the following options:

MaxIterations

10000

how many elements to generate at most

As long as only numeric iterators are used, Table[expr,spec₁,…] is effectively equivalent to ResourceFunction["TableWhile"][expr,spec₁,…].

As ResourceFunction["TableWhile"] uses Do internally, loop control functions such as Continue, Break, … might affect the result in ways that are not expected.

Examples

Basic Examples (3)

Generate all primes less than 100:

In[1]:=

Out[1]=

Generate all Fibonacci numbers below 1000, where the index has the form 3m+1:

In[2]:=

Out[2]=

Generate numbers of the form n^n-2 below a billion:

In[3]:=

$ResourceFunction["TableWhile"][n^(n - 2), {n, # <= 10^9 &}]$

Out[3]=

Computing an explicit iteration boundary is not possible:

In[4]:=

Out[4]=

Scope (3)

Generate reciprocals of the counting numbers until their mean falls below 0.1:

In[5]:=

Out[5]=

Check that the mean is indeed larger than 0.1:

In[6]:=

Out[6]=

Adding the next number would bring the mean below 0.1:

In[7]:=

Out[7]=

Generate random numbers as long as they are below 0.8:

In[8]:=

Out[8]=

Generate several such lists and plot their length distribution:

In[9]:=

Out[9]=

Generate polygonal numbers PolygonalNumber[r,n] for each r until their total exceeds 1000, or the individual numbers exceed 200. Stop increasing r when fewer than five numbers are generated:

In[10]:=

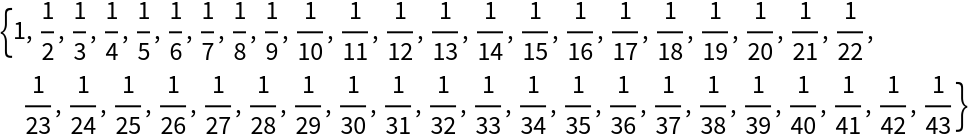
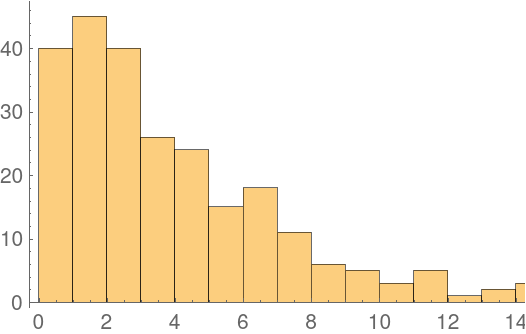
ResourceFunction["TableWhile"][
PolygonalNumber[r, n],
{r, 2, Length/*GreaterEqualThan[5]}, {n, {LessThan[200], Total/*LessThan[1000]}}
]

Out[10]=

Options (2)

MaxIterations (2)

With the default setting MaxIterations→10000, only 10,000 elements will be generated:

In[11]:=

In[12]:=

Out[12]=

Set MaxIterations to a higher value to generate all elements:

In[13]:=

In[14]:=

Out[14]=

Properties and Relations (1)

The result of TableWhile can often be emulated by generating a sufficiently long list and applying TakeWhile to it. However, this can be inefficient and elements might be missed:

In[15]:=

$list = ResourceFunction["TableWhile"][Sqrt[ Prime[n]], {n, 1, LessThan[1000], 2}, MaxIterations -> \[Infinity]]; // AbsoluteTiming$