Wolfram Function Repository

Instant-use add-on functions for the Wolfram Language

Function Repository Resource:

 FractionalOrderD

Source Notebook

Compute the fractional derivative of an expression

Contributed by: Oleg Marichev & Paco Jain (Wolfram Research)

ResourceFunction["FractionalOrderD"][f,{x,α}]

gives the α-order fractional integro-derivative of f with respect to x.

Details

There are different ways of defining the fractional integro-derivative. The current implementation uses the Riemann-Liouville formulation, defined by:
ResourceFunction["FractionalOrderD"] automatically maps over lists in its first argument.

Examples

Basic Examples (5) 

Compute a fractional derivative of a power function:

In[1]:=
ResourceFunction["FractionalOrderD"][x^2, {x, 3/2}]
Out[1]=

The first-order fractional derivative is equivalent to differentiation:

In[2]:=
ResourceFunction["FractionalOrderD"][x^2, {x, 1}]
Out[2]=
In[3]:=
D[x^2, x]
Out[3]=

The negative-first-order fractional derivative is equivalent to indefinite integration:

In[4]:=
ResourceFunction["FractionalOrderD"][x^2, {x, -1}]
Out[4]=
In[5]:=
Integrate[x^2, x]
Out[5]=

Compute the fractional derivative of symbolic order α of an exponential function:

In[6]:=
ResourceFunction["FractionalOrderD"][E^x, {x, \[Alpha]}]
Out[6]=

Compute the fractional derivative of symbolic order α of a logarithmic function:

In[7]:=
ResourceFunction["FractionalOrderD"][Log[x], {x, \[Alpha]}]
Out[7]=

Scope (1) 

FractionalOrderD works for both numeric and symbolic orders:

In[8]:=
ResourceFunction["FractionalOrderD"][x^n, {x, \[Alpha]}]
Out[8]=
In[9]:=
ResourceFunction["FractionalOrderD"][x^n, {x, 7/3}]
Out[9]=

Possible Issues (2) 

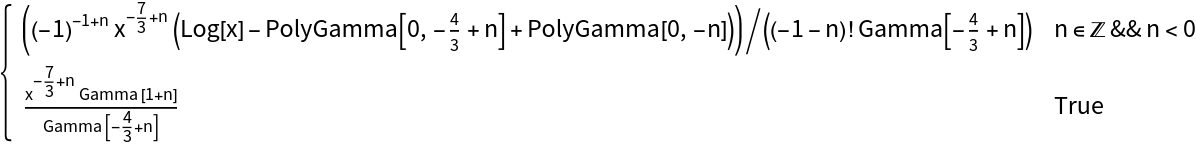FractionalOrderD may return results in terms of inactivated symbols like Sum, Product, Table, MeijerG, etc:

In[10]:=
res1 = ResourceFunction["FractionalOrderD"][ ChebyshevT[n, x], {x, \[Alpha]}]
Out[10]=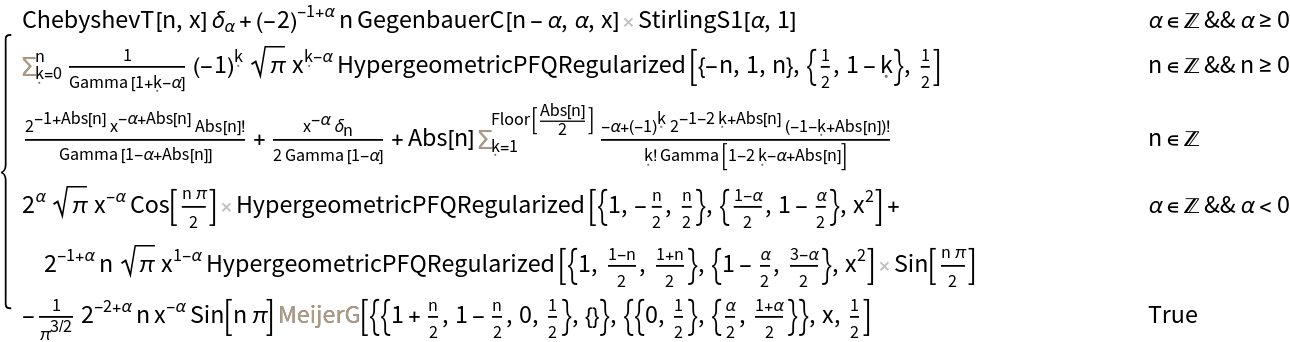
In[11]:=
res2 = ResourceFunction["FractionalOrderD"][ E^-\[FormalZ]^\[FormalM], {\[FormalZ], \[Alpha]}]
Out[11]=

In order to use such expressions, first substitute appropriate values of symbolic parameters and then apply Activate:

In[12]:=
res1 /. {n -> -2} // Activate
Out[12]=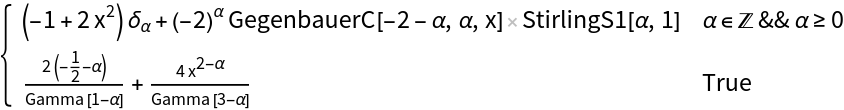
In[13]:=
res2 /. {\[FormalM] -> 3} // Activate
Out[13]=

In cases where only partial evaluation is possible, results may be returned that contain unevaluated FractionalOrderD expressions:

In[14]:=
ResourceFunction[ "FractionalOrderD"][(E^x Gamma[-x, x])/Gamma[-x], {x, \[Beta]}]
Out[14]=

Interactive Examples (1) 

Varying α from 0 to -1 smoothly interpolates between a function and its derivative:

In[15]:=
f[x] := x^3 Sin[x]; Manipulate[ Plot[Evaluate@{f[x], D[f[x], x], ResourceFunction["FractionalOrderD"][f[x], {x, m}]}, {x, 0, 5}], {m, 0, -1}, SaveDefinitions -> True]
Out[15]=

Neat Examples (1) 

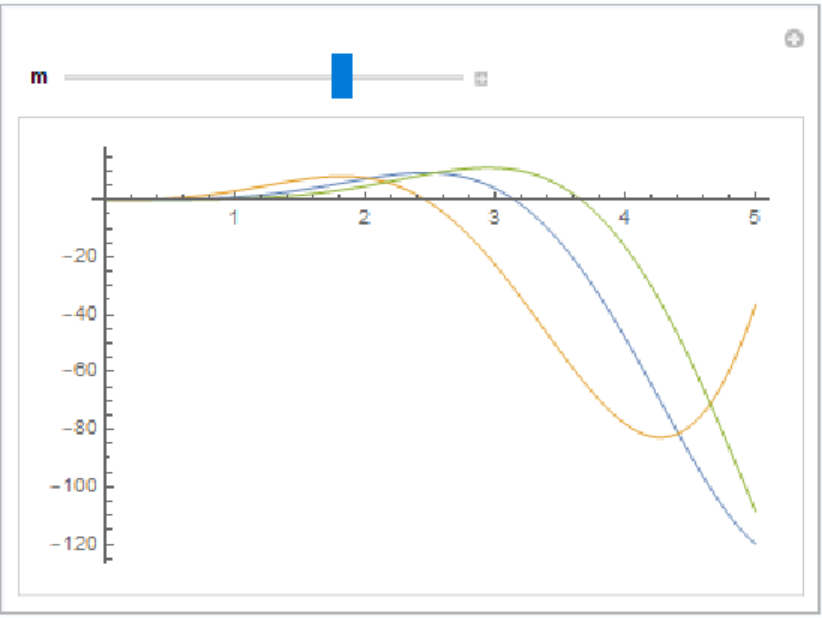Create a table of fractional derivatives:

In[16]:=
flist = {E^(x), x^2, Log[x], Sin[x], ArcTan[x], Cosh[x], ArcCosh[x], EllipticE[x], BesselJ[0, x]};
In[17]:=
Grid[Join[{{f[x], "FractionalOrderD"[f[x], {x, n}]}}, Transpose[{flist, ResourceFunction["FractionalOrderD"][flist, {x, n}]}]], Background -> {None, {{None, GrayLevel[.9]}}, {{1, 1} -> Hue[.6, .4, 1], {1, 2} -> Hue[.6, .4, 1]}}, BaseStyle -> {FontFamily -> Times, FontSize -> 12}, Dividers -> All, FrameStyle -> Hue[.6, .4, .8], Spacings -> {2, 1}] // TraditionalForm
Out[17]=

Publisher

Wolfram|Alpha Math Team

Version History

  • 3.2.0 – 14 August 2023
  • 3.1.4 – 07 November 2022
  • 3.1.3 – 11 October 2022
  • 3.1.2 – 11 October 2022
  • 3.1.1 – 23 August 2022
  • 3.1.0 – 23 August 2022
  • 3.0.0 – 23 August 2022
  • 2.1.0 – 11 September 2021
  • 2.0.0 – 05 October 2020
  • 1.0.0 – 23 September 2020

Related Resources

Author Notes

There are different ways of defining the fractional integro-derivative. The current implementation uses the Riemann-Liouville formulation. Another frequently-used definition, the Grunwald-Letnikov formulation may be implemented in a future version.

To view the full source code for this and related functions, evaluate the following:

In[1]:=
SystemOpen[ DirectoryName[ FindFile["WolframAlphaMath`SpecialFunctionsAndCalculus`"]]]

License Information