Function Repository Resource:

FindCombinatorProof

Attempt to find a proof of a theorem in combinatory logic using a given combinatory calculus

Contributed by: Jonathan Gorard

ResourceFunction["FindCombinatorProof"][thm,<|"Combinators"→comb,"Rules"→rules|>]

tries to find an equational proof of the combinatory logic theorem thm using the combinators comb and reduction rules rules.

ResourceFunction["FindCombinatorProof"][thm,calc]

tries to find an equational proof of the combinatory logic theorem thm using the named combinatory calculus calc.

Details and Options

If ResourceFunction["FindCombinatorProof"][thm,calc] succeeds in deriving the theorem thm from the combinatory calculus calc, then it returns a ProofObject expression. If it succeeds in showing that the theorem cannot be derived from the combinatory calculus, it returns a Failure object. Otherwise, it may not terminate unless time constrained.

ResourceFunction["FindCombinatorProof"] accepts both standard (named) combinatory calculi and arbitrary calculi specified via combinator reduction rules.

ResourceFunction["FindCombinatorProof"] accepts both individual theorems and lists of theorems.

ResourceFunction["FindCombinatorProof"] has the following options:

TimeConstraint

Infinity

how much time to allow

If ResourceFunction["FindCombinatorProof"] exceeds the specified time constraint, it returns a Failure object.

ResourceFunction["FindCombinatorProof"][thm,calc] uses the Knuth-Bendix completion algorithm to prove that the theorem thm follows from the reduction rules of the combinatory calculus calc.

Examples

Basic Examples (3)

Prove an elementary theorem about the single-variable fixed-point (y) combinator, with the reduction rule explicitly specified:

In[1]:=

Out[1]=

Show the abstract proof network, with tooltips showing the intermediate expressions:

In[2]:=

Out[2]=

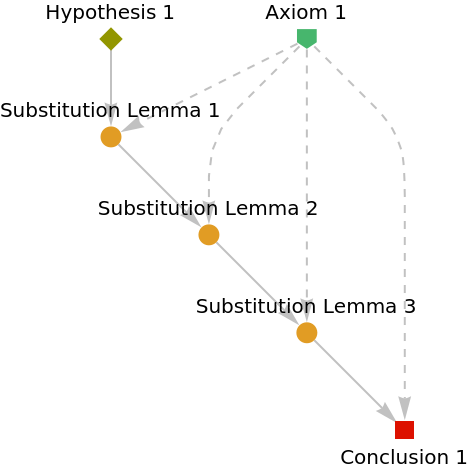
Show the complete list of proof steps as a Dataset object:

In[3]:=

Out[3]=

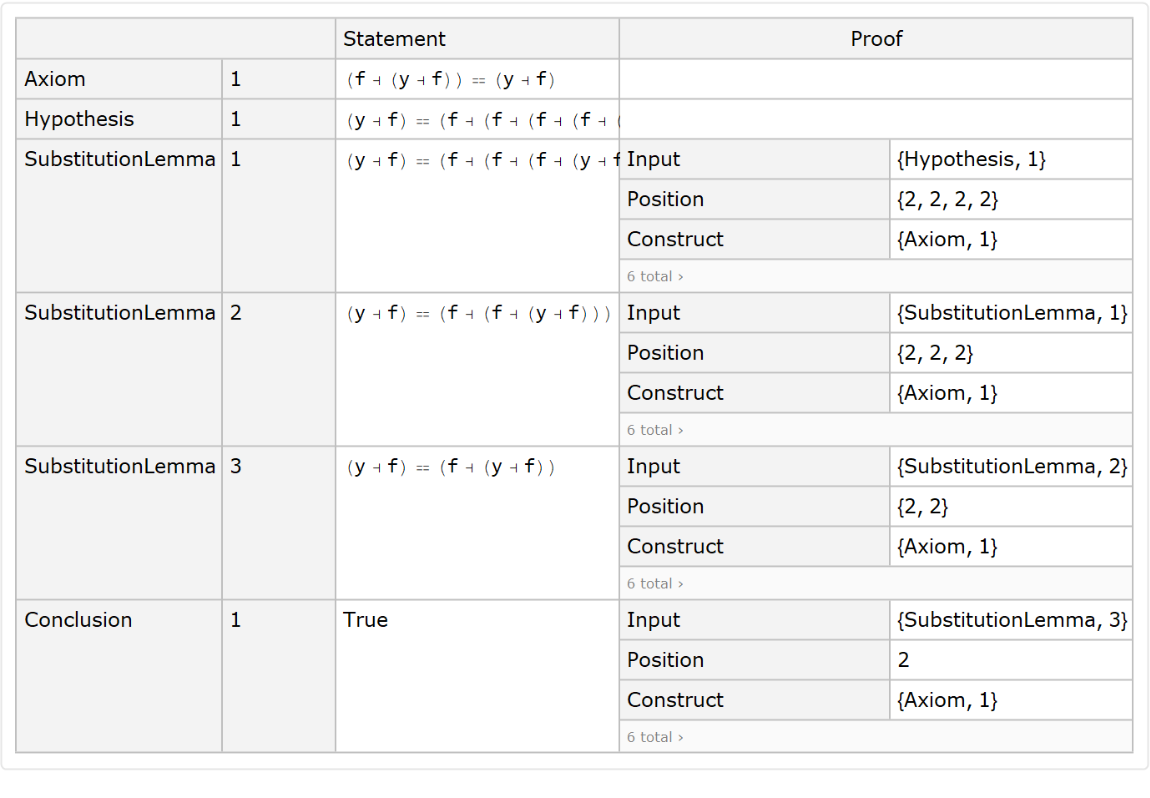
Typeset a natural language argument:

In[4]:=

Out[4]=

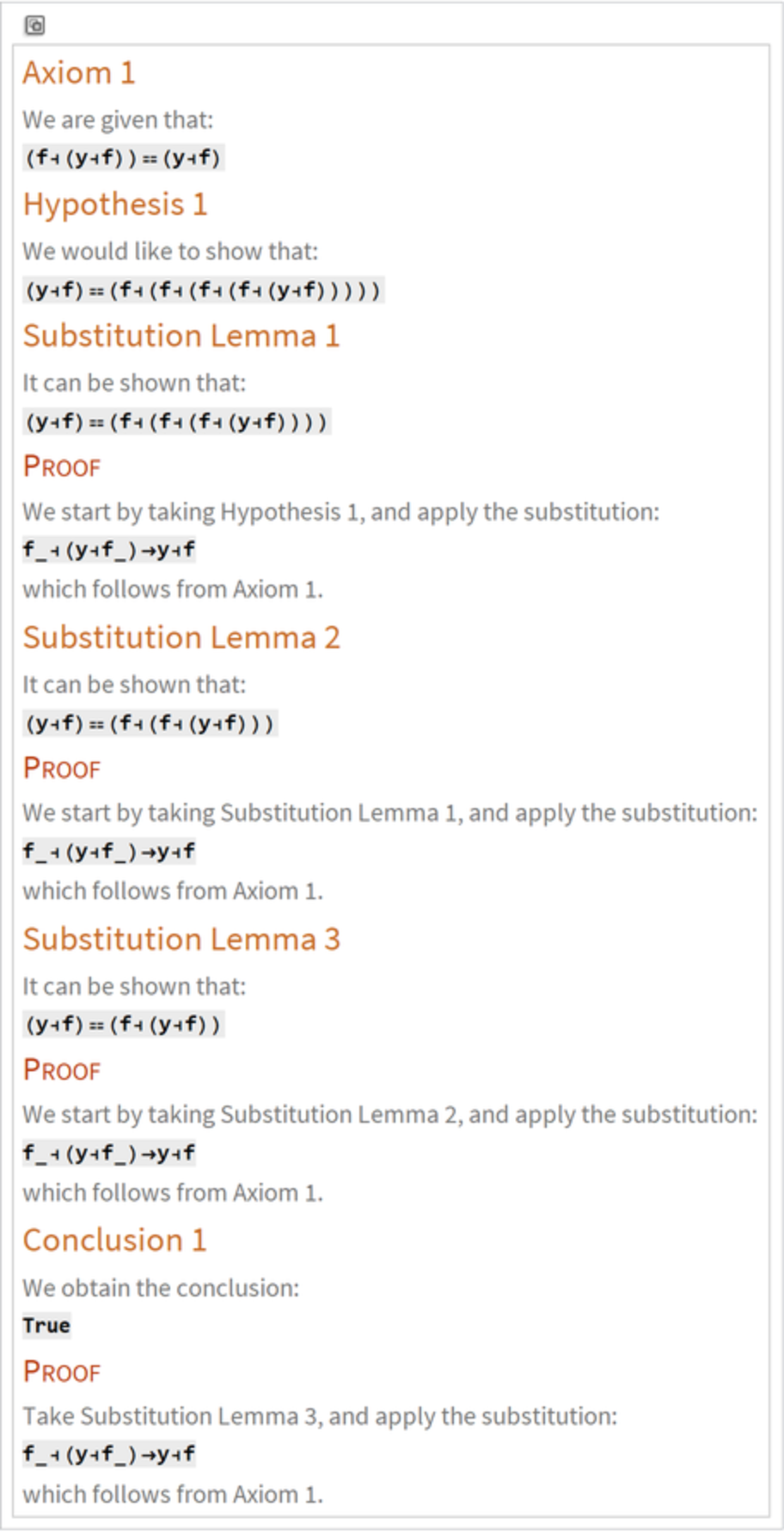
Prove a more sophisticated theorem involving the S-K combinatory calculus:

In[5]:=

proof = ResourceFunction["FindCombinatorProof"][
s[s[s[s]]][s][s][k] == s[k[s[s][s[s[s]]][k]]][
k[k[s[s][s[s[s]]][k]]][
s[s][k[s[k][s[s[s]][k]]]][k[k[s[k][s[s[s]][k]]]]]]], <|
"Combinators" -> {s, k}, "Rules" -> {s[x][y][z] == x[z][y[z]], k[x][y] == x}|>]

Out[5]=

Show the abstract proof network:

In[6]:=

Out[6]=

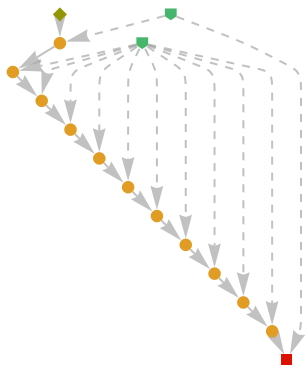
Prove a theorem using one of FindCombinatorProof's built-in combinatory calculi (Schönfinkel's B-C-I calculus):

In[7]:=

$proof = ResourceFunction[ "FindCombinatorProof"][\[FormalC][\[FormalI]][\[FormalB][\[FormalX]][\[FormalI]][\[FormalZ]]][\[FormalY]] == \[FormalY][\[FormalX][\[FormalZ]]], "BCI"]$

Out[7]=

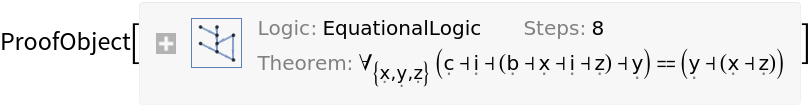
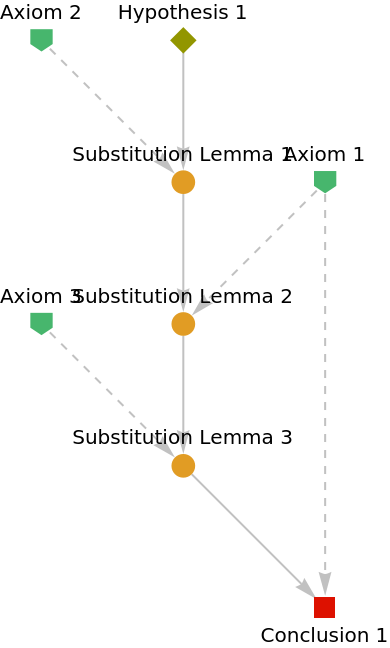
Show the abstract proof network:

In[8]:=

Out[8]=

Scope (7)

Show that a combinator equivalence proposition cannot be derived from a given combinatory calculus:

In[9]:=

Out[9]=

Named Combinatory Calculi (6)

FindCombinatorProof supports a variety of named combinatory calculi, including the single-variable fixed-point (y) combinator:

In[10]:=

$ResourceFunction[ "FindCombinatorProof"][\[FormalY][\[FormalF]] == \[FormalF][\[FormalF][\[FormalF][\[FormalY][\[FormalF]]]]], "Y"]$

Out[10]=

The two-variable fixed-point (y) combinator:

In[11]:=

$ResourceFunction[ "FindCombinatorProof"][\[FormalY][\[FormalF]][\[FormalY][\[FormalX]]] == \[FormalY][\[FormalF]][\[FormalX][\[FormalX][\[FormalX][\[FormalY][\[FormalX]]]]]], "Y2"]$

Out[11]=

The S-K calculus:

In[12]:=

$ResourceFunction[ "FindCombinatorProof"][\[FormalS][\[FormalS][\[FormalS][\[FormalS]]]][\[FormalS]][\[FormalS]][\[FormalK]] == \[FormalS][\[FormalS][\[FormalS]]][\[FormalK]][\[FormalS][\[FormalS]][\[FormalS][\[FormalS][\[FormalS]]]][\[FormalK]]], "SK"]$

Out[12]=

The S-K-I calculus:

In[13]:=

$ResourceFunction[ "FindCombinatorProof"][\[FormalS][\[FormalK][\[FormalS]][\[FormalI]]][\[FormalS][\[FormalK]][\[FormalK]][\[FormalI]]][\[FormalX]][\[FormalY]] == \[FormalX][\[FormalY]][\[FormalX][\[FormalY]]], "SKI"]$

Out[13]=

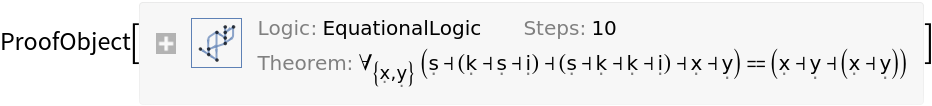
Schönfinkel's B and C combinators:

In[14]:=

$ResourceFunction[ "FindCombinatorProof"][\[FormalC][\[FormalK]][\[FormalB][\[FormalX]][\[FormalK]][\[FormalZ]]][\[FormalY]] == \[FormalK][\[FormalY]][\[FormalX][\[FormalK][\[FormalZ]]]], "BC"]$

Out[14]=

The B-C-I calculus:

In[15]:=

$ResourceFunction[ "FindCombinatorProof"][\[FormalC][\[FormalI]][\[FormalB][\[FormalX]][\[FormalI]][\[FormalZ]]][\[FormalY]] == \[FormalY][\[FormalX][\[FormalZ]]], "BCI"]$

Out[15]=

Initial Conditions (1)

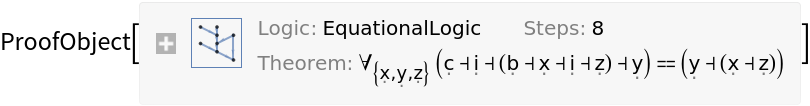
FindCombinatorProof accepts both individual theorems and lists of theorems:

In[16]:=

Out[16]=

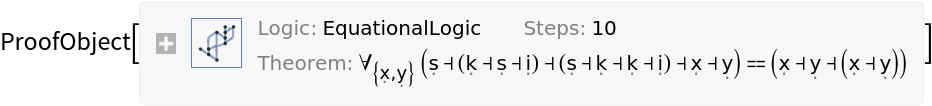
In[17]:=

$ResourceFunction[ "FindCombinatorProof"][{\[FormalS][\[FormalK][\[FormalS]][\[FormalI]]][\[FormalS][\[FormalK]][\[FormalK]][\[FormalI]]][\[FormalX]][\[FormalY]] == \[FormalX][\[FormalY]][\[FormalX][\[FormalY]]], \[FormalS][\[FormalK][\[FormalS]][\[FormalI]]][\[FormalS][\[FormalK]][\[FormalK]][\[FormalI]]][\[FormalY]][\[FormalX]] == \[FormalY][\[FormalX]][\[FormalY][\[FormalX]]]}, "SKI"]$

Out[17]=

Options (1)

TimeConstraint (1)

Use TimeConstraint→t to limit the computation time to t seconds:

In[18]:=

$ResourceFunction[ "FindCombinatorProof"][\[FormalS][\[FormalS][\[FormalS][\[FormalS]]]][\[FormalS]][\[FormalS]][\[FormalK]] == \[FormalS][\[FormalK][\[FormalS][\[FormalS]][\[FormalS][\[FormalS][\[FormalS]]]][\[FormalK]]]][\[FormalK][\[FormalK][\[FormalS][\[FormalS]][\[FormalS][\[FormalS][\[FormalS]]]][\[FormalK]]]][\[FormalS][\[FormalS]][\[FormalK][\[FormalS][\[FormalK]][\[FormalS][\[FormalS][\[FormalS]]][\[FormalK]]]]][\[FormalK][\[FormalK][\[FormalS][\[FormalK]][\[FormalS][\[FormalS][\[FormalS]]][\[FormalK]]]]]]]], "SK", TimeConstraint -> 0.001]$

Out[18]=

In[19]:=

Out[19]=

Properties and Relations (1)

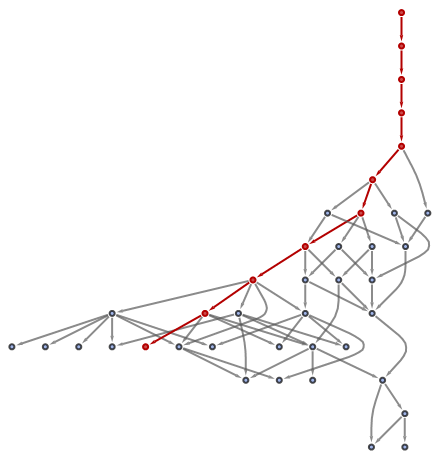
FindCombinatorProof will return a proof object for a particular theorem if and only if the associated path exists in the corresponding multiway system:

In[20]:=

Out[20]=

In[21]:=

$mwGraph = ResourceFunction["MultiwayCombinator"][{s[x_][y_][z_] :> x[z][y[z]], k[x_][y_] :> x}, s[s[s[s]]][s][s][k], 10, "StatesGraphStructure"]$

Out[21]=

In[22]:=

Out[22]=

In[23]:=

Out[23]=

Publisher

Jonathan Gorard

Version History

1.0.0 – 04 December 2020

Source Metadata

Citation:
- Stephen Wolfram (2002), A New Kind of Science.
- Stephen Wolfram (2020), "A Class of Models with the Potential to Represent Fundamental Physics".
- Jonathan Gorard (2020), "Some Relativistic and Gravitational Properties of the Wolfram Model".
- Jonathan Gorard (2020), "Some Quantum Mechanical Properties of the Wolfram Model".

Related Resources

License Information

This work is licensed under a Creative Commons Attribution 4.0 International License

Wolfram Function Repository

FindCombinatorProof

Details and Options