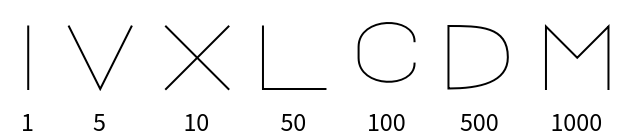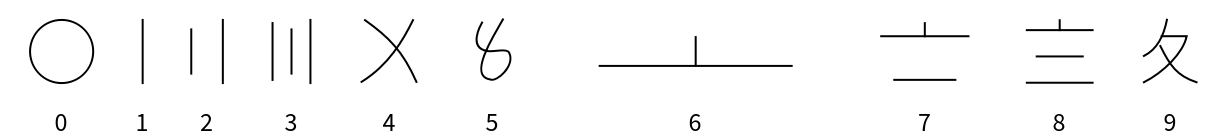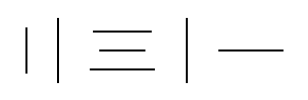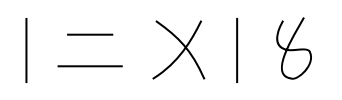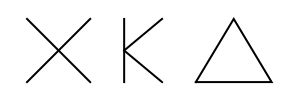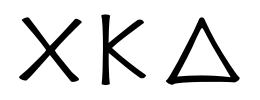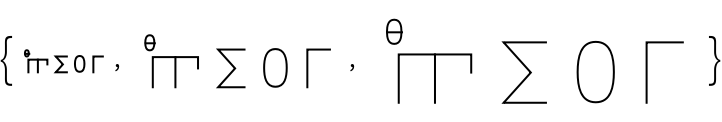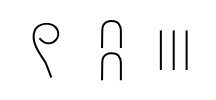Scope (4)
By default, numerals are returned as an Interpretation of a Graphics object:
Returning numerals with Interpretation allows basic computations with the numerals:
The optional third argument also allows you to return numerals as simple Graphics objects or as a list of Graphics objects:
For Roman numerals only, String is also a supported output type:
Aegean (1)
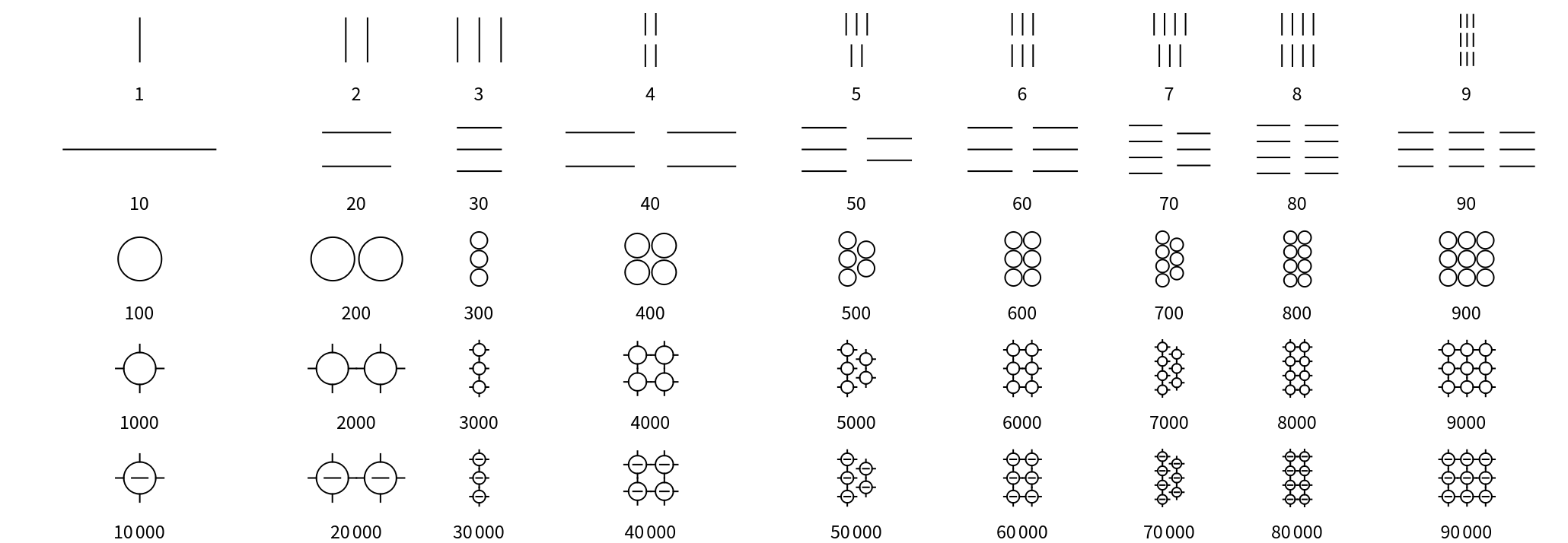
Aegean numerals are a base-10 number system. There are symbols for each power of ten from 1 to 10,000:
Aztec (2)
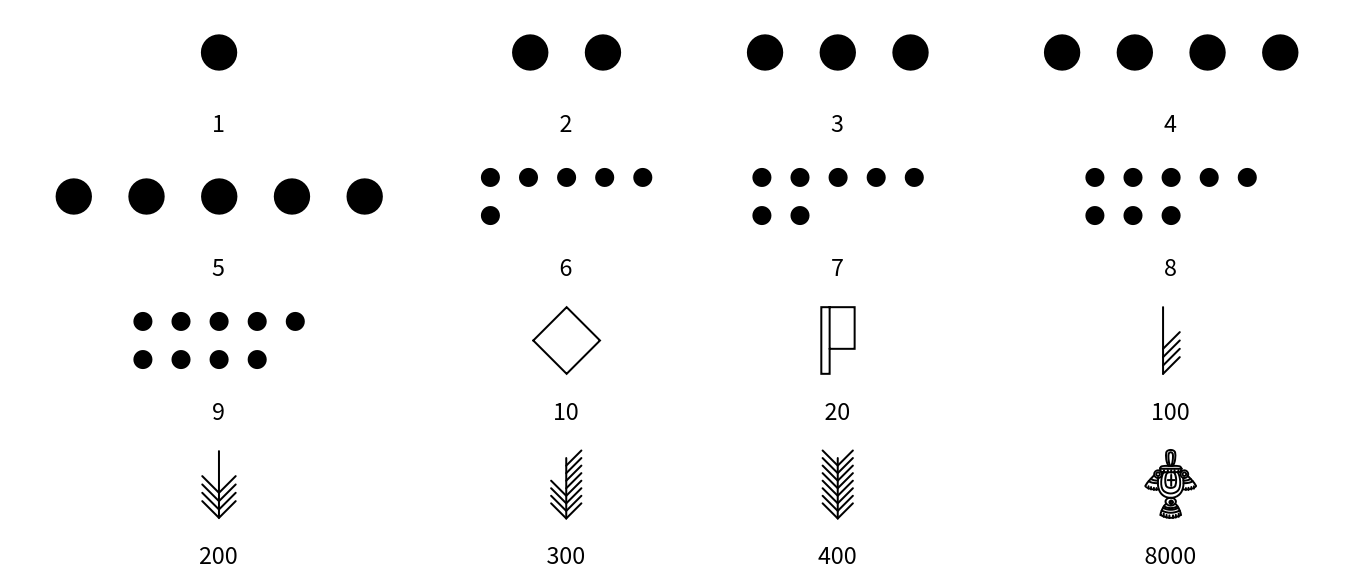
Aztec numerals are a base-20 system, with additional symbols for 10 and small multiples of 100. There are symbols for the following values: a dot represents 1, a lozenge represents 10, a flag represents 20, feathers with increasing numbers of barbs represent 100, 200, 300 and 400, and a xiquipilli (bag) represents 8000:
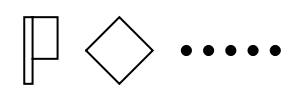
Most integers can be represented in multiple ways. For example, 35 can be 35 dots (35 × 1); three lozenges with five dots (3 × 10 + 5 × 1); or one flag, one lozenge and five dots (1 × 20 + 1 × 10 + 5 × 1). NumeralRepresentation returns just the representation with the fewest number of symbols needed:
Babylonian (2)
Babylonian numerals are a base-60 system. There is a symbol for a unit and a symbol for a ten:
Here are the Babylonian numerals for 1 - 60:
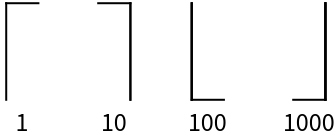
Cistercian (2)
Cistercian numerals are a base-10 system where each number from 1 - 9999 has a unique symbol. The symbols have four parts (top right, top left, bottom right and bottom left), each of which corresponds to a place value (ones, tens, hundreds and thousands, respectively):
Here are the Cistercian numerals for 1 - 9:
Egyptian (2)
Egyptian numerals are a base-10 number system. There are symbols for each power of ten from 0 to 6 (i.e., 1 to 1,000,000), each made of a figure representing an object:
Up to the ten thousands, the Egyptian symbols are arranged in rows or columns to form each place value. For hundred thousands and millions, NumeralRepresentation just places the repeated symbols in a single row:
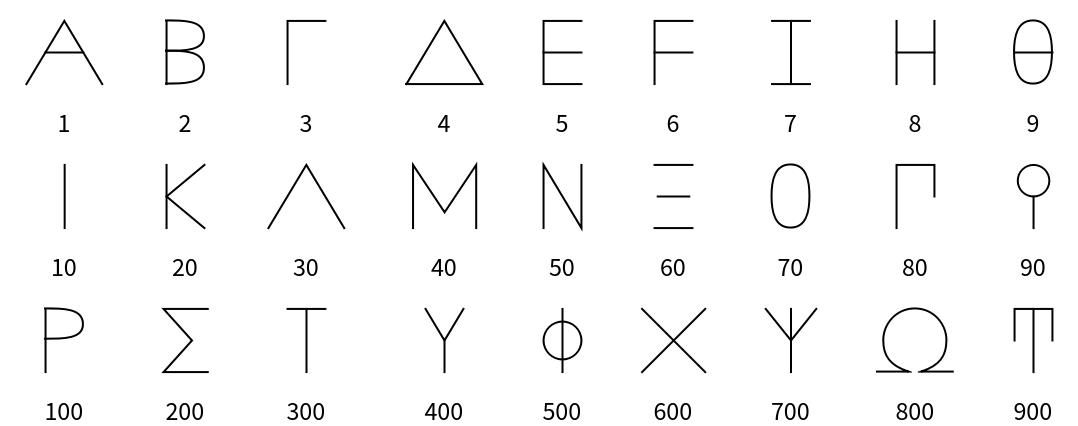
Greek (2)
Greek numerals are a positional base-10 numeral system. There are separate characters for the digits 1 - 9, the multiples of 10 from 10 - 90, and the multiples of 100 from 100 - 900:
There is a single character that represents 1000, and multiples of 1000 are distinguished by adding an additional character to its upper left:
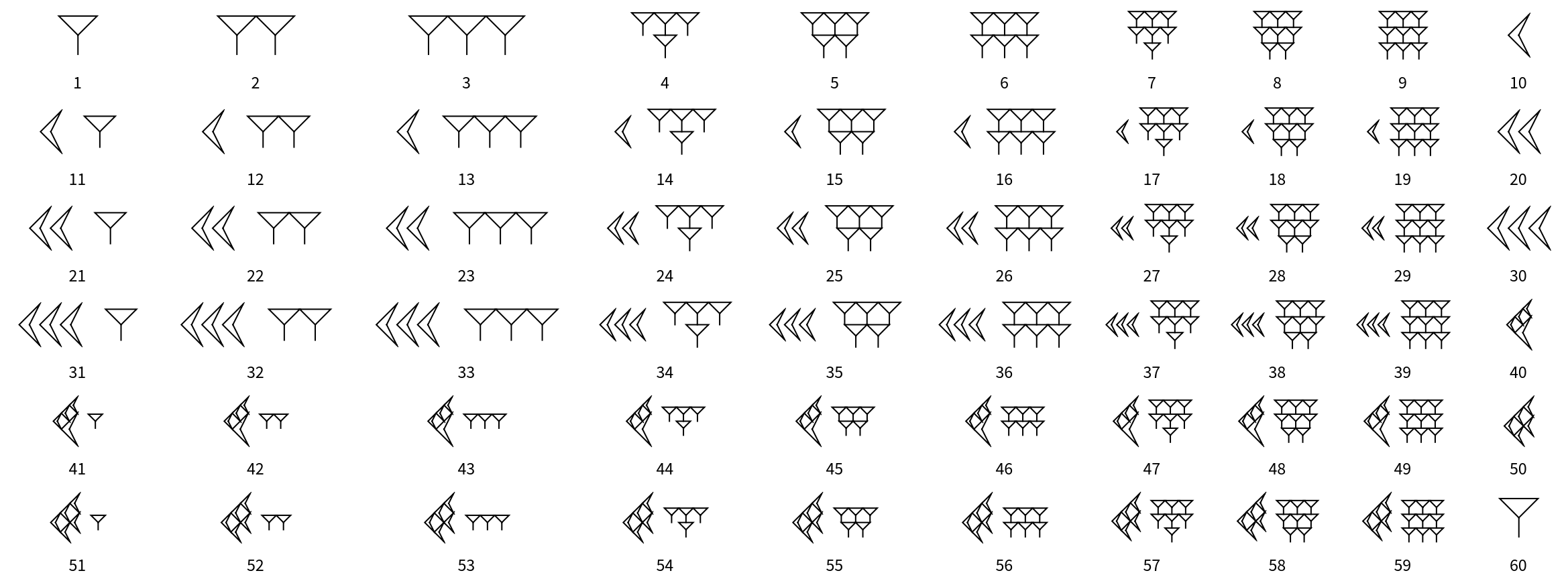
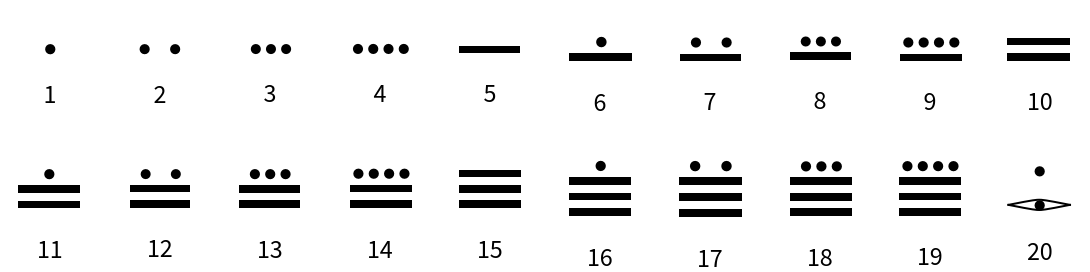
Mayan (3)
Mayan numerals are a positional base-20 system. There symbols include a dot for one, a bar for five and a shell for zero:
Numerals are stacked vertically from bottom to top. The bottom group of symbols represents ones, the next group up represents twenties, the next group up represents four-hundreds (202), and so on. For example, the numeral 1357 is written as follows:
Here are the Mayan numerals from 1 to 20:
Roman (2)
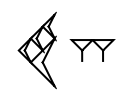
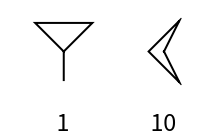
Roman numerals are a base-ten number system comprised of seven symbols (1, 5, 10, 50, 100, 500, 1000):
A vinculum (overbar) represents multiplication by 1000 and can be used to represent large numbers:
Suzhou (2)
Suzhou numerals are a positional base-10 system, with separate symbols for the digits 0 - 9. Here are all of the Suzhou numeral symbols:
When the characters for ones, twos or threes are written consecutively, they are rotated so as not to run together. For example:
Options (8)
NumeralStyle (1)
Each numeral type can be displayed in either a "Simplified" or a "Handwritten" style:
Tooltip (3)
Setting Tooltip→True is the same as setting Tooltip→"PlaceValue", where each digit in the numeral has a tooltip displaying its place value:
Setting Tooltip→"SymbolValue" adds a tooltip to each symbol within each digit, showing its value:
Setting Tooltip→"SymbolName" adds a tooltip to each symbol within each digit, showing a string describing each symbol:
FontColor (1)
The FontColor option controls the color in which the numerals are rendered:
FontSize (1)
The FontSize option controls the size in which the numerals are rendered:
Spacings (2)
The Spacings option controls the spacing between the numerals:
For the vertically-arranged Mayan numeral system, Spacings adjusts the vertical spacing of the numerals:
Possible Issues (3)
Several of the numeral systems have an upper limit on the values which have representations:
Several of the numeral systems have no symbol that represents zero:
Because it is used in the arrangement of the numerals themselves, the PlotRange option of Graphics cannot be given to NumeralRepresentation:


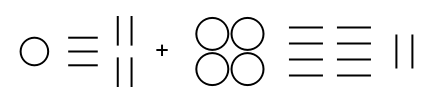
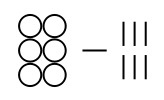

![Grid[Thread[
Labeled[ResourceFunction["NumeralRepresentation"][#, "Aegean"], #]] & /@ (Table[Range[9], 5] * 10^Range[0, 4])]](https://www.wolframcloud.com/obj/resourcesystem/images/b72/b7251248-32c9-4b73-b006-d0b066cf235d/08d369a36e9905da.png)
![Grid[Thread[
Labeled[ResourceFunction["NumeralRepresentation"][#, "Aztec"], #]] & /@ Partition[Join[Range[9], {10, 20, 100, 200, 300, 400, 8000}], 4]]](https://www.wolframcloud.com/obj/resourcesystem/images/b72/b7251248-32c9-4b73-b006-d0b066cf235d/096301ebdf54b020.png)
![Grid[Thread[
Labeled[ResourceFunction["NumeralRepresentation"][#, "Babylonian"], #]] & /@ Partition[Range[60], 10]]](https://www.wolframcloud.com/obj/resourcesystem/images/b72/b7251248-32c9-4b73-b006-d0b066cf235d/1d979fc4e3ffec76.png)
![Row[Thread[
Labeled[ResourceFunction["NumeralRepresentation"][#, "Cistercian"], #]] & /@ (10^Range[0, 3]), Spacer[20]]](https://www.wolframcloud.com/obj/resourcesystem/images/b72/b7251248-32c9-4b73-b006-d0b066cf235d/656047adb64711dc.png)

![Row[Thread[
Labeled[ResourceFunction["NumeralRepresentation"][#, "Egyptian"], #]] & /@ Prepend[10^Range[0, 6], 0], " "]](https://www.wolframcloud.com/obj/resourcesystem/images/b72/b7251248-32c9-4b73-b006-d0b066cf235d/5b340c3cbd8c3312.png)
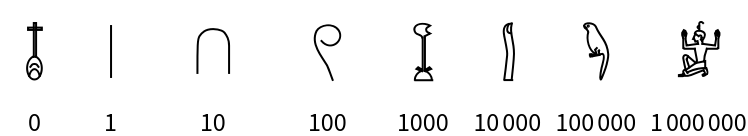
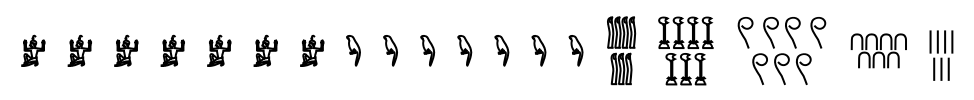
![Grid[Thread[
Labeled[ResourceFunction["NumeralRepresentation"][#, "Greek"], #]] & /@ (Table[Range[9], 3] * 10^Range[0, 2])]](https://www.wolframcloud.com/obj/resourcesystem/images/b72/b7251248-32c9-4b73-b006-d0b066cf235d/662d027314d0e202.png)


![Grid[{
{"3 \[Times] (1 \[Times] 400)", ResourceFunction["NumeralRepresentation"][3, "Mayan"]},
{"(1 \[Times] (5 \[Times] 20)) + (2 \[Times] (1 \[Times] 20))", ResourceFunction["NumeralRepresentation"][7, "Mayan"]},
{"(3 \[Times] (5 \[Times] 20)) + (2 \[Times] (1 \[Times] 20))", ResourceFunction["NumeralRepresentation"][17, "Mayan"]}
}]](https://www.wolframcloud.com/obj/resourcesystem/images/b72/b7251248-32c9-4b73-b006-d0b066cf235d/0a0c6447b79a4ffa.png)
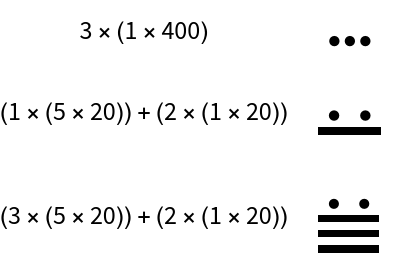
![Row[Thread[
Labeled[ResourceFunction["NumeralRepresentation"][#, "Roman"], #]] & /@ {1, 5, 10, 50, 100, 500, 1000}]](https://www.wolframcloud.com/obj/resourcesystem/images/b72/b7251248-32c9-4b73-b006-d0b066cf235d/3bcb043f3ee99c94.png)