Basic Examples (4) 

When the first card on the flop is 4♢ the best hole cards are any other pair of 4s, which are treated as equally strong:

In[1]:=

Out[1]=

When no cards have yet been dealt, the best hole cards are 'Pocket Aces':

In[2]:=

Out[2]=

Find the 10 best hole card combinations for a flop of K♡, 8♢, 5♠:

In[3]:=

Out[3]=

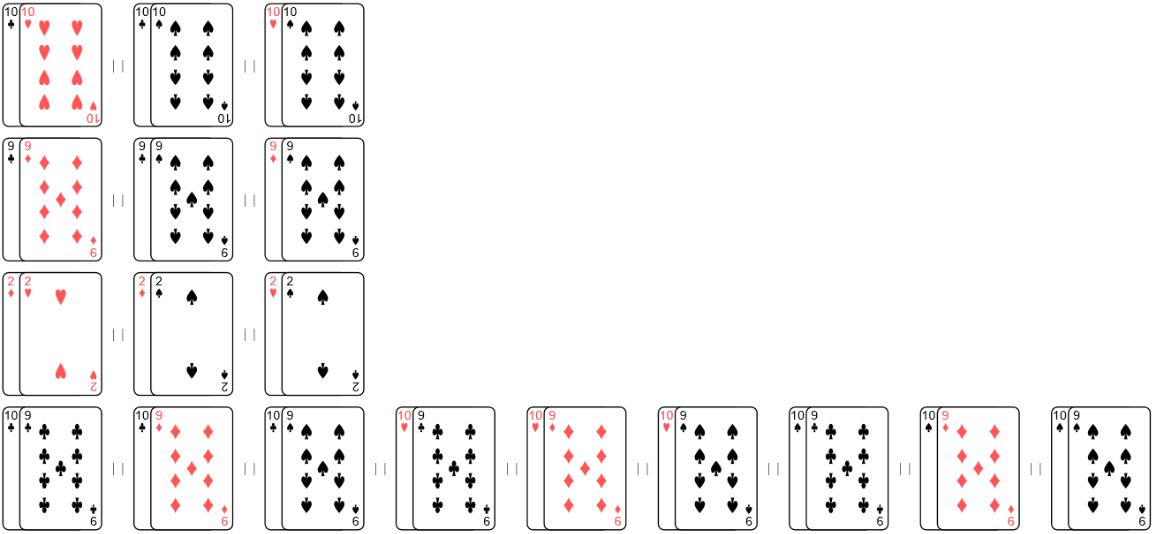
The many different full houses resulting from a 'wet board' (a board that can make many different strong hands) are ranked :

In[4]:=

Out[4]=

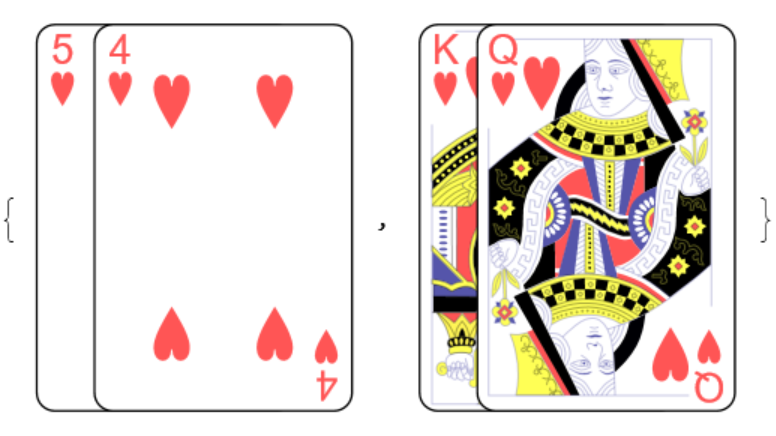
The elusive royal flush:

In[5]:=

Out[5]=

Scope (3) 

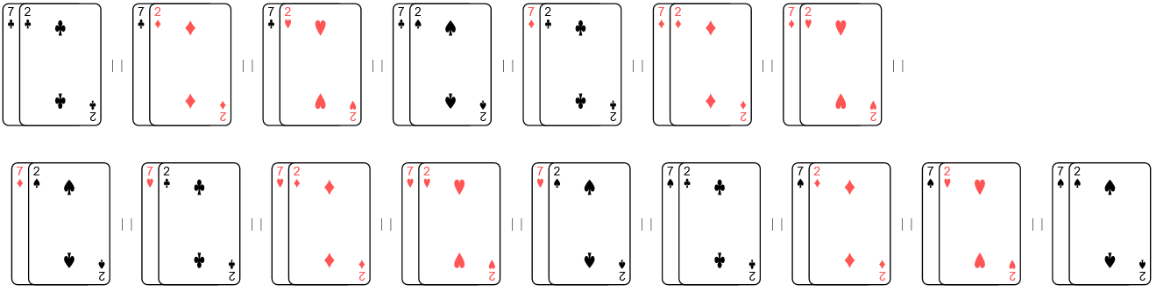
If the community card list has two or fewer cards, then straights, flushes, or full houses cannot be constructed. Here, the top-ranked hole cards result in three-of-a-kind, followed by two-pair, followed by one-pair:

In[6]:=

Out[6]=

An Ace-to-5 straight (also known as the "wheel") is treated as weaker than a 2-to-6 straight, since Ace is 'low' here:

In[7]:=

Out[7]=

A straight flush beats an Ace-high flush:

In[8]:=

Out[8]=

Options (2) 

Setting the option "ShowGraphic" → True calls PlayingCardGraphic:

In[9]:=

Out[9]=

The graphics are returned in the same format as the lists:

In[10]:=

Out[10]=

In[11]:=

Out[11]=

Applications (2) 

If four cards are already on the table, we technically only need to use one of our hole cards to make a complete five-card hand. The 14th strongest entry (A♣/♡/♠) represents this. This is usually referred to as "Ace-X". Weaker hole card combinations such as {A♣/♡/♠, 8♣/♢/♡/♠} are included since swapping the 9♣ for 8♣/♡/♠ actively makes the hand 'weaker'. It is also worth noting that for this example, {Q♣/♢/♡/♠, J♣/♢/♡/♠} makes two distinct straights: T-to-A and 9-to-K. However, only the strongest-performing instance of a given hole card combination is used in the final ranking, so {Q♣/♢/♡/♠, J♣/♢/♡/♠} appears at the first position rather than both the first and second position:

In[12]:=

Out[12]=

If all five cards have been dealt, all possible combinations of using zero, one, or both hole cards are checked and ranked. Therefore, it takes a couple of minutes to run. The 29th strongest entry here includes an empty list, representing not using hole cards at all! This means that the five community cards alone would beat any hands made using hole cards below 29th position. This is clear if one looks at the hands below 29th position and recognizes that they represent swapping Q♣ on the board with a lower-ranked card:

In[13]:=

Out[13]=

Properties and Relations (2) 

Use a Take-like specification to find the 4th-9th strongest hole cards:

In[14]:=

Out[14]=

Alternatively, find the weakest possible hole cards:

In[15]:=

Out[15]=

Possible Issues (3) 

The number of cards in the input must not exceed five:

In[16]:=

If there are repeated instances of a given card, it is flagged as invalid since a poker game typically uses a single deck:

In[17]:=

An error is flagged for invalid ranks or suits:

In[18]:=

In[19]:=

Neat Examples (5) 

In the 2006 film Casino Royale, there is a now famous Texas hold 'em poker scene in which four players miraculously have very strong hands, resulting in a $115 million pot. We can use this function to explore their relative strength.
First, we note the hole cards that each player held:

In[20]:=

We also need the five cards that were on the table:

In[21]:=

It would be difficult to know exactly how many unique rankings there are, so we can use Span (;;):

In[22]:=

Finally, we find the position within this ranked list of our players' hands:

In[23]:=

Out[23]=

We can now find the number of unique rankings:

In[24]:=

Out[24]=