Wolfram Function Repository
Instant-use add-on functions for the Wolfram Language
Function Repository Resource:
Compute the Ricci scalar for a metric
ResourceFunction["RicciScalar"][M,{u,v}] computes the Ricci scalar for a metric M in terms of variables u and v. |
The monkey saddle surface:
| In[1]:= |
| In[2]:= |
| Out[2]= |
Plot the surface:
| In[3]:= |
| Out[3]= | 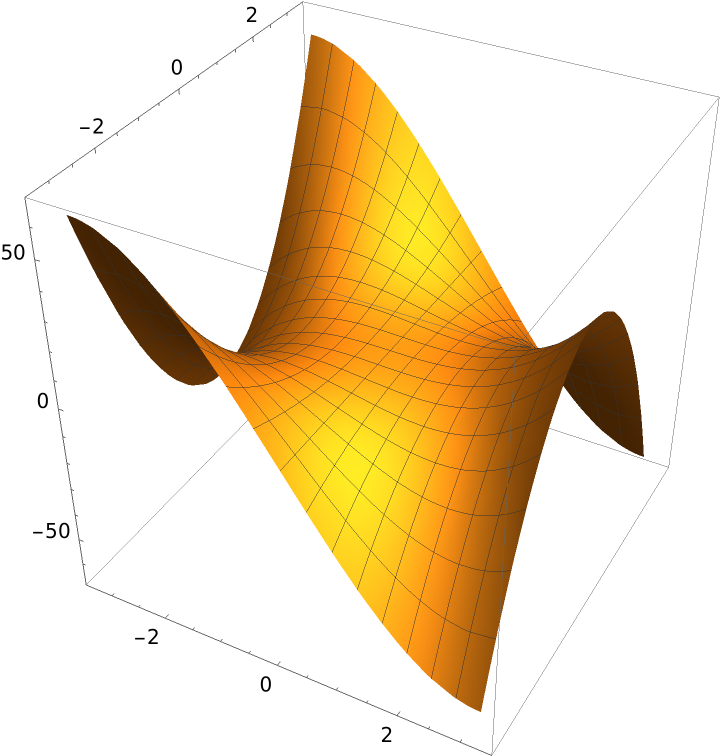 |
The covariant basis:
| In[4]:= |
| Out[4]= |
The metric tensor:
| In[5]:= |
| Out[5]= |
The metric tensor in normal form:
| In[6]:= |
| Out[6]= |
Compute the Ricci scalar from the metric:
| In[7]:= |
| Out[7]= |
Alternately, compute the Ricci scalar via the Ricci curvature:
| In[8]:= |
| Out[8]= |
Contracting an index gives the Ricci scalar:
| In[9]:= |
| Out[9]= |
Confirm that this is equivalent to the Ricci curvature computed previously from the metric directly:
| In[10]:= |
| Out[10]= |
The metric tensor for an arbitrary metric:
| In[11]:= |
| Out[11]= |
The Brioschi formula for the Gaussian curvature:
| In[12]:= | ![BrioschiCurvature[M_, {u_, v_}] :=
Module[{U, V, A, B, ee, ff, gg},
ee = M[[1, 1]]; ff = M[[1, 2]]; gg = M[[2, 2]]; A1 = {-\!\(
\*SubscriptBox[\(\[PartialD]\), \(v, v\)]ee\) + 2 \!\(
\*SubscriptBox[\(\[PartialD]\), \(u, v\)]ff\) - \!\(
\*SubscriptBox[\(\[PartialD]\), \(u, u\)]gg\), \!\(
\*SubscriptBox[\(\[PartialD]\), \(u\)]ee\), 2 \!\(
\*SubscriptBox[\(\[PartialD]\), \(u\)]ff\) - \!\(
\*SubscriptBox[\(\[PartialD]\), \(v\)]ee\)}; A2 = {\!\(
\*SubscriptBox[\(\[PartialD]\), \(v\)]ff\) - \!\(
\*SubscriptBox[\(\[PartialD]\), \(u\)]gg\)/2, ee, ff}; A3 = {\!\(
\*SubscriptBox[\(\[PartialD]\), \(v\)]gg\)/2, ff, gg}; A = {A1/2, A2, A3}; B1 = {0, \!\(
\*SubscriptBox[\(\[PartialD]\), \(v\)]ee\), \!\(
\*SubscriptBox[\(\[PartialD]\), \(u\)]gg\)}; B2 = {\!\(
\*SubscriptBox[\(\[PartialD]\), \(v\)]ee\)/2, ee, ff}; B3 = {\!\(
\*SubscriptBox[\(\[PartialD]\), \(u\)]gg\)/2, ff, gg}; B = {B1/2, B2, B3}; AB = (Det[A] - Det[B])/Det[M]^2; Simplify[AB]]](https://www.wolframcloud.com/obj/resourcesystem/images/b53/b537df69-e607-43c9-b84a-5167bfb65618/15a945b721db7266.png) |
Compute the Ricci scalar for the arbitrary metric:
| In[13]:= |
| Out[13]= | 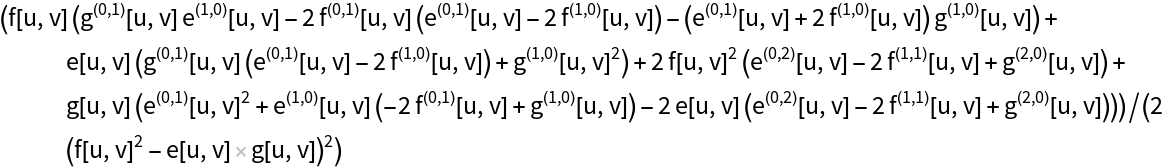 |
Prove that this coincides with twice the Gaussian curvature:
| In[14]:= |
| Out[14]= |
This work is licensed under a Creative Commons Attribution 4.0 International License