Wolfram Function Repository
Instant-use add-on functions for the Wolfram Language
Function Repository Resource:
Compute the polar decomposition of a matrix
ResourceFunction["PolarDecomposition"][m] yields the polar decomposition for a numerical matrix m. The result is a list {q,s}, where q is a column orthonormal matrix and s is a Hermitian positive semidefinite matrix. |
Compute the polar decomposition for a 4×3 matrix:
| In[1]:= |
![ResourceFunction["PolarDecomposition"][( {
{1., 2., 3.},
{1., 5., 6.},
{1., 8., 9.},
{1., 11., 12.}
} )]](https://www.wolframcloud.com/obj/resourcesystem/images/b16/b1601306-0972-4773-929e-732692497a90/314a447b098c386a.png)
|
| Out[1]= |

|
Compute the polar decomposition of a complex matrix:
| In[2]:= |
|
| Out[2]= |

|
A matrix with entries having 20-digit precision:
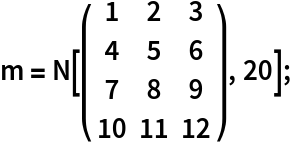
The polar decomposition is computed using the full 20-digit precision of the input:
| In[3]:= |
|
| Out[3]= |

|
A random 5×4 matrix m:
Compute its polar decomposition:
| In[4]:= |
|
| Out[4]= |

|
The columns of q are orthonormal:
| In[5]:= |
|
| Out[5]= |
|
The matrix s is Hermitian positive semidefinite:
| In[6]:= |
|
| Out[6]= |
|
The matrix s is equal to MatrixPower[ConjugateTranspose[m].m,1/2]:
| In[7]:= |
|
| Out[7]= |
|
m is equal to q.s:
| In[8]:= |
|
| Out[8]= |
|
If the matrix m is Hermitian positive semidefinite, then q is equal to the identity matrix, and s is equal to m:
| In[9]:= |
|
| Out[9]= |
|
| In[10]:= |
|
| Out[10]= |
|
PolarDecomposition only works with approximate numerical matrices:
| In[11]:= |
|
| Out[11]= |
|
| In[12]:= |
|
| Out[12]= |
|
This work is licensed under a Creative Commons Attribution 4.0 International License