Wolfram Function Repository
Instant-use add-on functions for the Wolfram Language
Function Repository Resource:
Compute a conchoid curve
ResourceFunction["ConchoidCurve"][c,p,d] computes one branch of the conchoid of the curve c with respect to the fixed point p and distance d. | |
ResourceFunction["ConchoidCurve"][c,p,d,-1] computes the other branch of the conchoid. |
Conchoid of a circle:
| In[1]:= |
|
| Out[1]= |
|
Plot one branch of the conchoid:
| In[2]:= |
|
| Out[2]= |
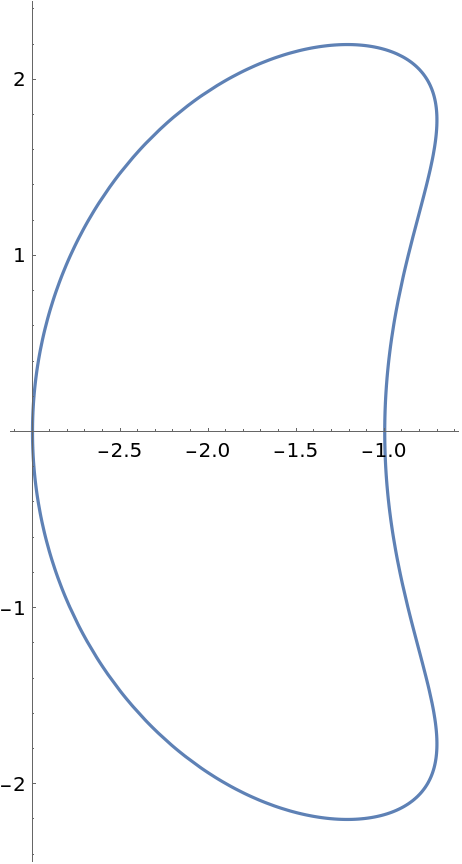
|
Plot the other branch:
| In[3]:= |
|
| In[4]:= |
|
| Out[4]= |
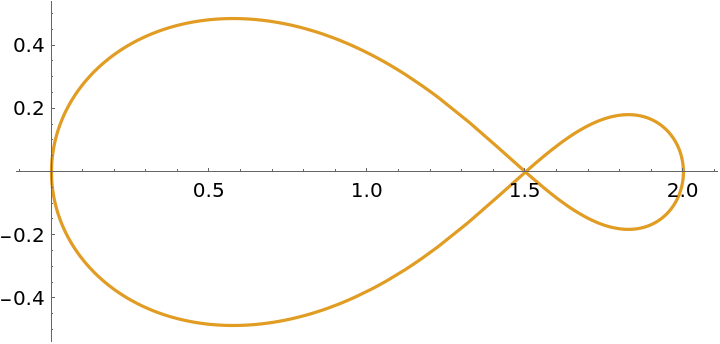
|
Show both branches together:
| In[5]:= |
|
| Out[5]= |
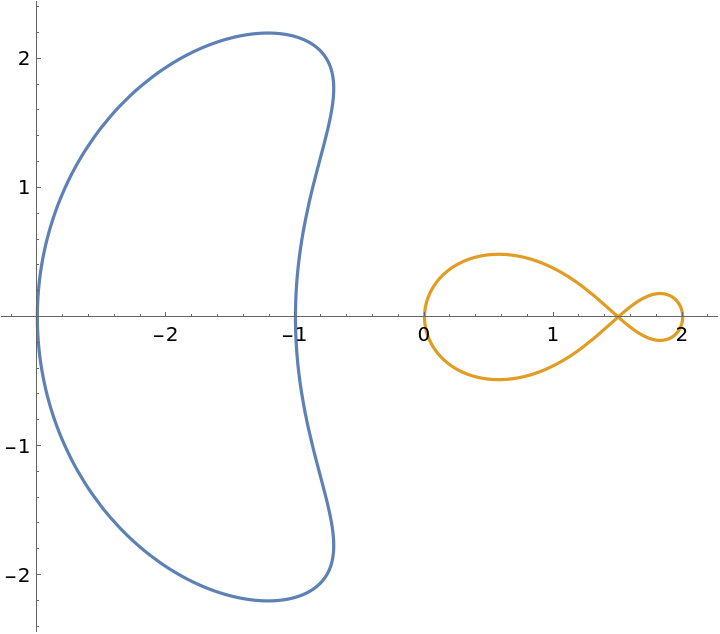
|
Find the implicit Cartesian equation of the conchoid:
| In[6]:= |
|
| Out[6]= |
|
The conchoid of Nicomedes is the conchoid of a line with respect to the origin:
| In[7]:= |
|
| Out[7]= |
|
| In[8]:= |
|
| Out[8]= |
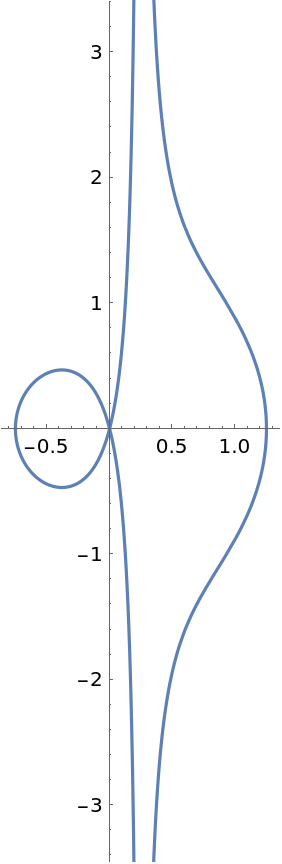
|
This work is licensed under a Creative Commons Attribution 4.0 International License