Wolfram Function Repository

Instant-use add-on functions for the Wolfram Language

Function Repository Resource:

 GraphRandomWalk

Source Notebook

Create a discrete or continuous time random walk on a graph

Contributed by: Daniel McDonald

ResourceFunction["GraphRandomWalk"][g,v,t]

returns a TemporalData object representing a random walk on the edge-weighted graph g starting at vertex v and going from time 0 to time t.

ResourceFunction["GraphRandomWalk"][g,v,t,n]

returns a TemporalData object representing n random walks.

Details and Options

GraphRandomWalk takes the Method option which can be set to either "Discrete" or "Continuous", defaulting to the former.
A discrete time random walk on a graph with positive edge weight function f has the walker move from their present vertex u to a neighboring vertex v with probability where the sum ranges over all neighbors w of u.
A continuous time random walk lasting total time t on a graph with edge weight function f has each edge uv assigned a list of ''step event'' times uniformly distributed in the time interval (0,t), with the average number of events per unit time equal to f(u,v) (i.e. according to a homogeneous Poisson point process with constant intensity f(u,v)), and has the walker step from the vertex they are occupying at time t0 to the neighboring vertex along the incident edge with the next ''step event'' time t1 occurring past t0.

Examples

Basic Examples (2) 

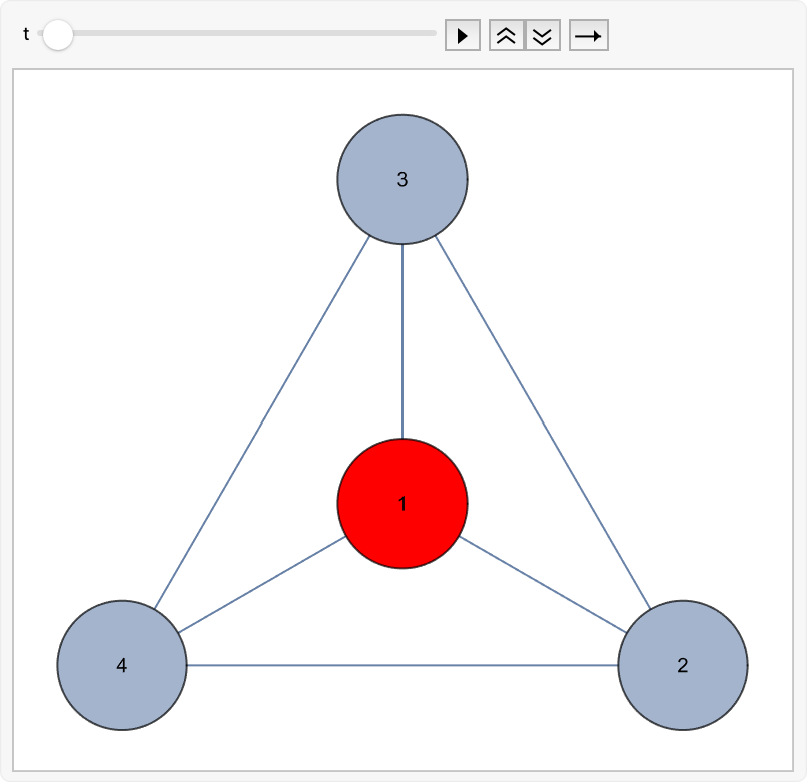
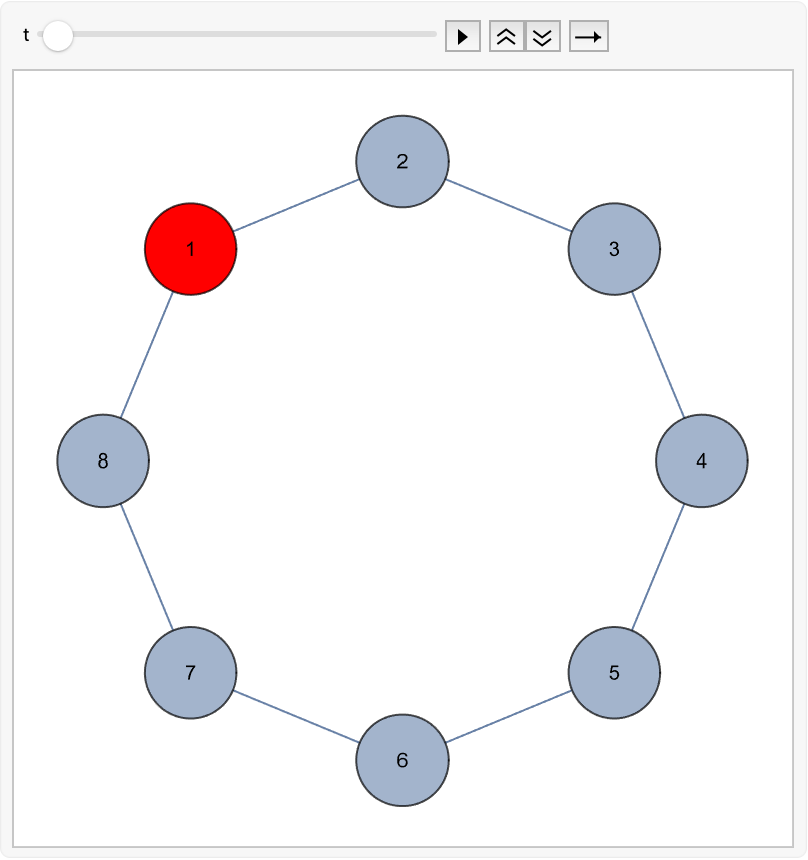
Create a discrete time random walk on a cycle graph with unit weight on each edge, starting at vertex 1 and lasting ten steps:

In[1]:=
ResourceFunction["GraphRandomWalk"][CycleGraph[8], 1, 10, Method -> "Discrete"]
Out[1]=

Extract the walk, which is a list where each element is a pair of the form {t,v}, representing a move to the vertex v at time t:

In[2]:=
%["Path", 1]
Out[2]=

Animate this walk:

In[3]:=
Animate[ Graph[CycleGraph[8], VertexStyle -> {Which @@ Join @@ MapApply[{t >= #1, #2} &, Reverse@%] -> Red}, VertexSize -> Large, VertexLabels -> Placed[Automatic, Center], EdgeLabels -> None], {t, %[[1, 1]], %[[-1, 1]]}, AnimationRunning -> False ]
Out[3]=

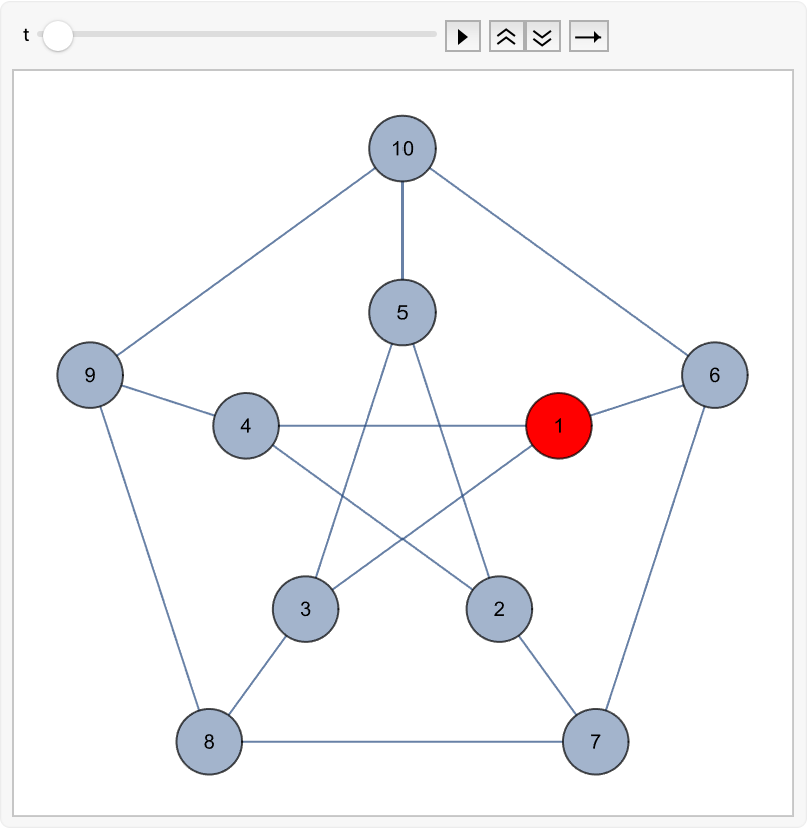
Create a continuous time random walk on the Petersen graph with unit weight on each edge, starting at vertex 1 and lasting from time t=0 to t=10:

In[4]:=
ResourceFunction["GraphRandomWalk"][PetersenGraph[5, 2], 1, 10, Method -> "Continuous"]
Out[4]=

Extract the walk, which is a list where each element is a pair of the form {t,v}, representing a move to the vertex v at time t:

In[5]:=
%["Path", 1]
Out[5]=

Animate this walk:

In[6]:=
Animate[ Graph[PetersenGraph[5, 2], VertexStyle -> {Which @@ Join @@ MapApply[{t >= #1, #2} &, Reverse@%] -> Red}, VertexSize -> Large, VertexLabels -> Placed[Automatic, Center], EdgeLabels -> None], {t, %[[1, 1]], %[[-1, 1]]}, AnimationRunning -> False ]
Out[6]=

Options (2) 

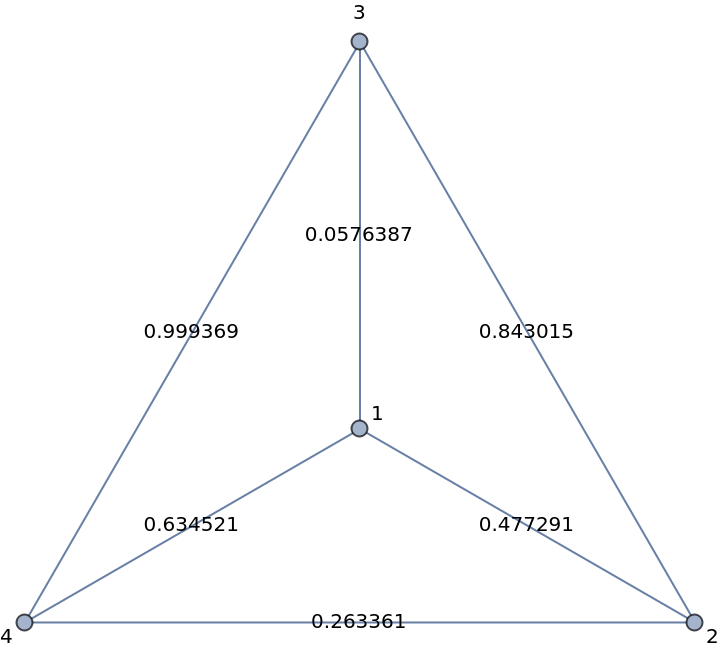
Create a weighted graph:

In[7]:=
gg = GridGraph[{4, 4}, EdgeWeight -> RandomReal[{0, 1}, 24], VertexLabels -> "Name", EdgeLabels -> "EdgeWeight"]
Out[7]=

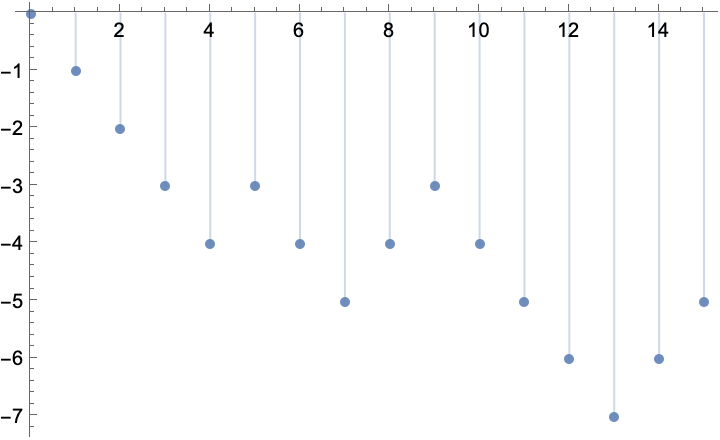
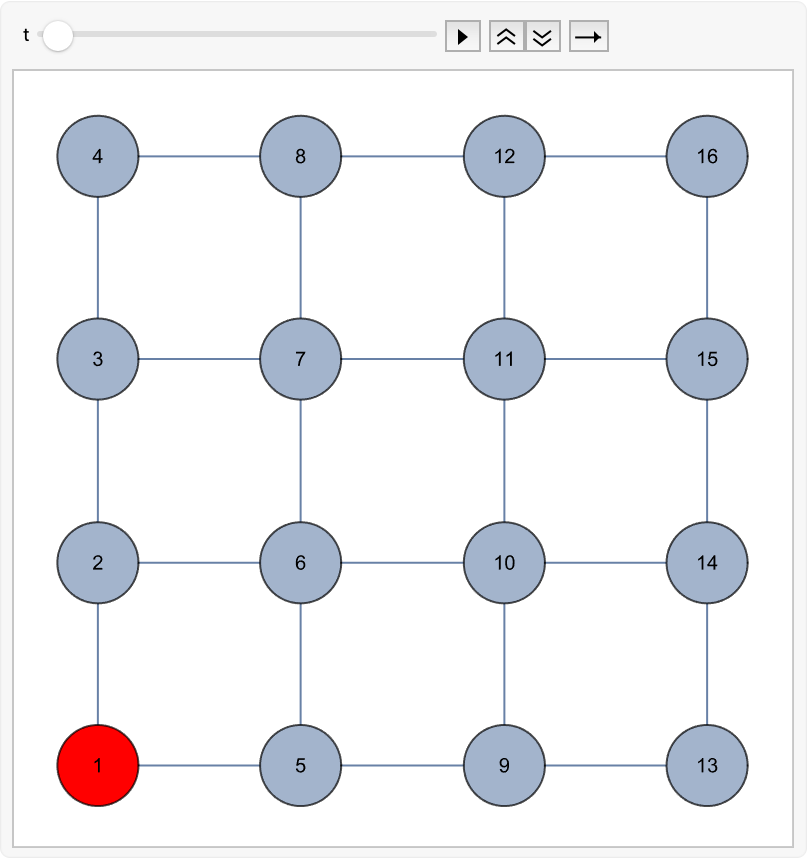
Create five discrete time random walks on the graph, each starting at vertex 1 and lasting ten steps:

In[8]:=
discreteWalks = ResourceFunction["GraphRandomWalk"][gg, 1, 10, 5, Method -> "Discrete"]
Out[8]=

Extract the first of these walks, a list where each element is a pair of the form {t,v}, representing a move to the vertex v at time t:

In[9]:=
discreteWalk1 = discreteWalks["Path", 1]
Out[9]=

Animate this walk:

In[10]:=
Animate[ Graph[gg, VertexStyle -> {Which @@ Join @@ MapApply[{t >= #1, #2} &, Reverse@discreteWalk1] -> Red}, VertexSize -> Large, VertexLabels -> Placed[Automatic, Center], EdgeLabels -> None], {t, discreteWalk1[[1, 1]], discreteWalk1[[-1, 1]]}, AnimationRunning -> False ]
Out[10]=

Create a weighted graph:

In[11]:=
cg = CompleteGraph[4, EdgeWeight -> RandomReal[{0, 1}, 6], VertexLabels -> "Name", EdgeLabels -> "EdgeWeight"]
Out[11]=

Create five continuous time random walks on the graph, each starting at vertex 1 and lasting from time t=0 to t=10:

In[12]:=
continuousWalks = ResourceFunction["GraphRandomWalk"][cg, 1, 10, 1, Method -> "Continuous"]
Out[12]=

Extract the first of these walks, a list where each element is a pair of the form {t,v}, representing a move to the vertex v at time t:

In[13]:=
continuousWalk1 = continuousWalks["Path", 1]
Out[13]=

Animate this walk:

In[14]:=
Animate[ Graph[cg, VertexStyle -> {Which @@ Join @@ MapApply[{t >= #1, #2} &, Reverse@continuousWalk1] -> Red}, VertexSize -> Large, VertexLabels -> Placed[Automatic, Center], EdgeLabels -> None], {t, continuousWalk1[[1, 1]], continuousWalk1[[-1, 1]]}, AnimationRunning -> False ]
Out[14]=

Properties and Relations (2) 

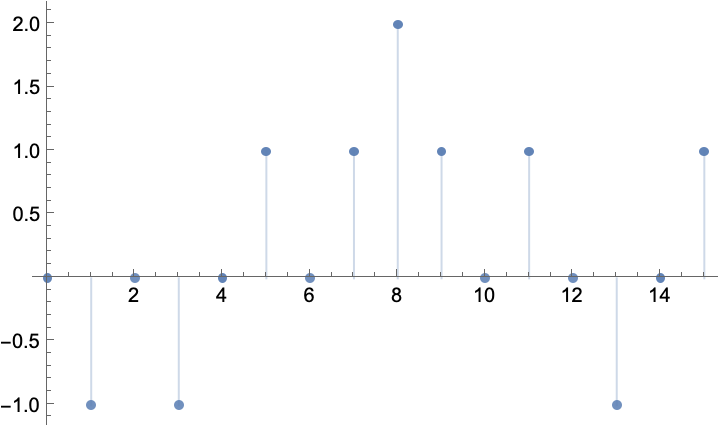
Create a one-dimensional discrete time random walk where the walker may either walk up or down:

In[15]:=
ListPlot[ ResourceFunction["GraphRandomWalk"][PathGraph[Range[-15, 15]], 0, 15, Method -> "Discrete"], Filling -> Axis]
Out[15]=

This is equivalent to using RandomWalkProcess:

In[16]:=
ListPlot[RandomFunction[RandomWalkProcess[.5], {0, 15}], Filling -> Axis]
Out[16]=

Possible Issues (2) 

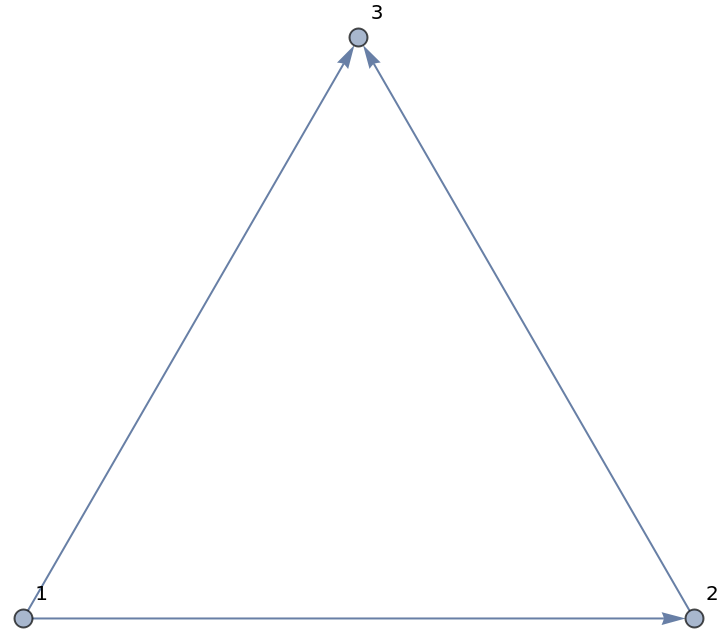
Consider a directed graph with a sink vertex:

In[17]:=
Graph[{1 -> 2, 1 -> 3, 2 -> 3}, VertexLabels -> "Name"]
Out[17]=

Arbitrary length discrete time random walks may not be possible, in which case the walks found may not have the designated number of steps, and if multiple walks are found they may have different lengths:

In[18]:=
ResourceFunction["GraphRandomWalk"][%, 1, 10, 8, Method -> "Discrete"]["Paths"]
Out[18]=

Publisher

Daniel McDonald

Requirements

Wolfram Language 13.0 (December 2021) or above

Version History

  • 1.0.0 – 06 August 2025

Related Resources

License Information